基于响应面方法的铁路纵断面优化技术

李晓娥

（中铁第四勘察设计院集团有限公司 武汉 430063）

铁路选线设计是铁路建设的先行，其目的是要确定线路最合适的空间位置，这一位置决定了铁路上建筑物的位置、工程数量的大小和施工的难易，也决定了列车运行的条件和运营成本的高低。选线设计的任务就在于比选出既满足铁路设计规范要求又使工程运营费用最小的设计方案［1］。随着电子计算机技术的发展，以及优化理论、模糊数学、神经网络和灰色理论等的逐步应用，现代铁路选线设计方法较以前传统方法有了很大的突破。目前，基于以上各种理论的设计方法都进行了较深入的研究，部分已形成商用软件，运用到设计实践中并且取得了一定的效果。其中，由于优化方法相对简单易懂，基于优化方法的铁路选线设计方法得到了最广泛的研究和应用。

1 问题的提出与研究方法

最优化就是从所有可能方案中选择最合理的一种以达到最优目的的方法。通俗地讲，也就是求解多元函数约束极值问题。其数学表达为［2］：

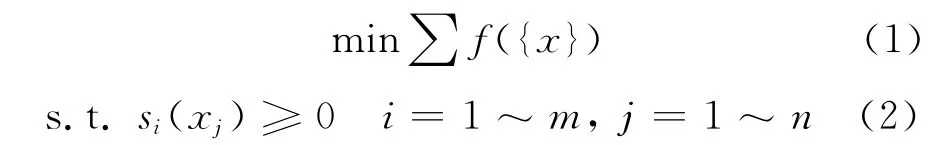
在线路的平面位置已定的条件下，不同的变坡点位置和高程将决定不同的纵断面设计方案。纵断面优化设计，就是从众多设计方案中选出一种最佳的变坡点位置和高程组合，使相关工程费用或换算运营费用最小。构造这一问题的数学模型必须解决以下3个问题：

（1）确定纵断面优化设计的变量。

（2）确定纵断面优化设计的目标函数。

（3）确定纵断面优化设计的约束条件。

其中，问题（1）和（3）比较容易解决。前已述及，纵断面优化设计的变量一般是指纵断面变坡点的位置和高程；而约束条件即是必须满足规范和其他各种技术经济要求，具体来说主要有坡段的最大坡度限制、相邻坡段的最大坡度差限制、变坡点高程限制以及变坡点位置限制等等［3］。

问题（2）中的工程费用或换算运营费用主要包括路基土石方费、挡墙工程费、桥梁工程费、隧道工程费、铁路用地费和其他费用。在方案确定阶段，不必精确计算相关费用。为了简化计算，可以采用各计算点的设计标高和施工标高的平方和作为生成链式线路平面的目标函数。即

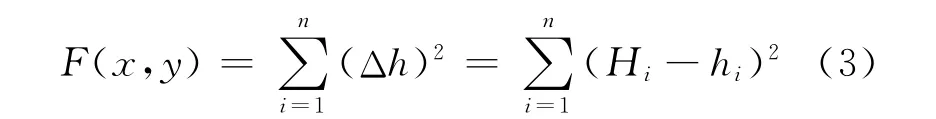
式中：x和y为线路各变坡点的位置和高程；n为变坡点个数；Hi为i点地面高程；hi为对应位置线路点设计高程。

对于表达式比较简单的目标函数，如式（3）可以直接写出目标函数的显式表达式，优化计算时目标函数对变量的梯度也可以直接求得；如果对于一个很复杂的问题如需精确计算工程费用时，无法写出目标函数的显式表达式，虽然目标函数值可以通过计算分别求得，但是其对变量的梯度却无法求得，优化求解将陷入困境。针对这一问题，本文提出一种基于响应面理论的铁路纵断面优化方法。

2 响应面方法

响应面方法是一项统计学的综合试验技术，用于处理若干变量对一个体系或结构的作用问题，也就是体系或结构的输入与输出的转换关系问题，用有限的试验来回归拟合一个关系式，代替结构的真实响应曲面。其思想是选用一个适当的明确表达的函数来近似代替一个不能明确表达的函数，也就是利用式（3）的计算结果来拟合一个具有明确表达式的响应面以代替未知的系统响应曲面，从而使得各种针对显式功能函数的分析方法可以应用于隐式功能函数问题的分析中［4］。在选择响应面表达式形式的时候，一方面要尽可能简洁，另一方面要能足够灵活地反映各种不同的真实曲面形状。通常有以下2种形式，表达式（4）为不含交叉项的二次多项式；表达式（5）为含有交叉项的二次多项式，所含的未知量个数分别为2n＋1和（n＋1）（n＋2）／2。

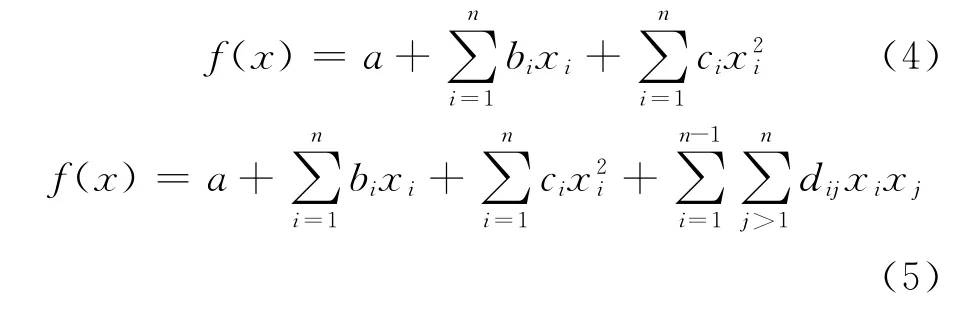
式中：n为设计变量的个数；a，bi，ci，di（i＝1，2，…，n）为待定因数。

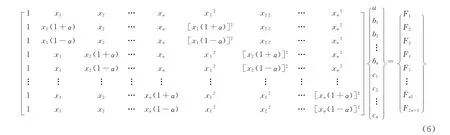
本文选取不含交叉项的二次多项式（4）作为响应面表达式。对于任意xi（i＝1，…，n），均可以xi（i＝1，…，n）为中心点，在n维坐标系的各轴上，对每个xj（j＝1，…，n，j≠i）左右各设置一个适当的偏量α，得到2n＋1个响应点，见图1。由此，可得2n＋1阶线性方程组，a，bi，ci（i＝1，2，…，n）可解。如选取式（4），形式较为简洁，计算方便，但由此可能带来计算精度的降低。计算经验表明，一般来说，选取这样的表达式是合适的。

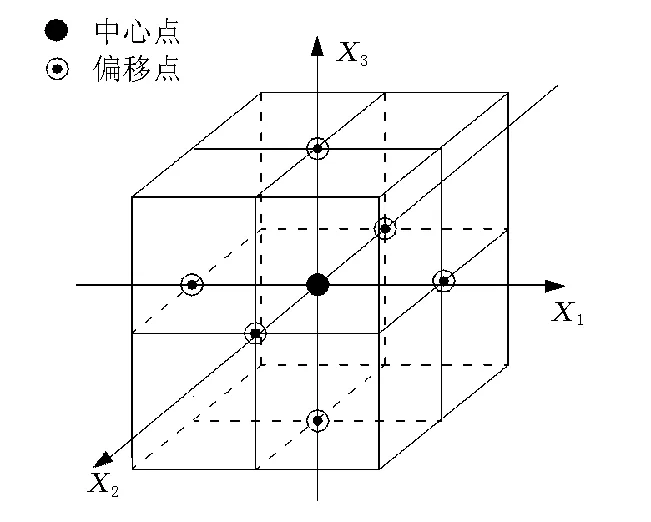
图1 目标函数（4）的变量空间（n＝3）

为了说明响应面方法的应用，本文对于可以直接写出显式表达式的式（3）也用响应面方法来拟合表达式。如式（4）所示，当设计变量为n时响应面表达式有2n＋1个待定系数需要确定。分别变化变量x1，x2，…，xn的值，根据式（3）计算得到函数值如式（6）右端项，构造2n＋1阶线性方程组如下：

式中：α为响应面偏量；a～cn为拟合多项式系数；F1～F2n＋1为目标函数值。

求解式（6）即得到拟合多项式，进而变量梯度可以求解，对问题的优化也就迎刃而解。

3 问题的优化求解

目前，对于优化问题式（1）的求解方法比较成熟［2］。在用响应面求得目标函数的显式表达式之后，目标函数对变量的梯度易求如式（7）所示，优化求解可采用梯度方法如“DFP”算法，此法是目前为止处理无约束优化问题的最有效的方法之一。

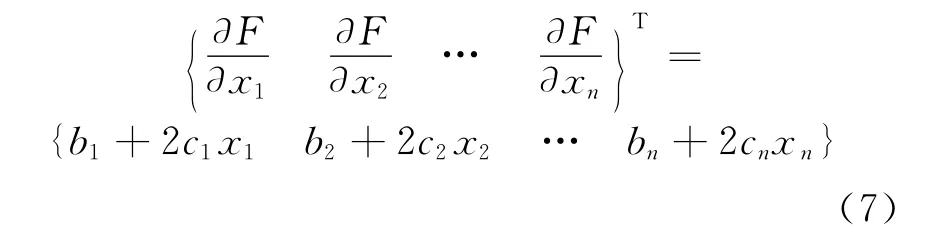
对于约束优化问题，本文采用内部惩罚函数法，又称内点法，它对企图从内部穿越容许集边界的点在目标函数中加入相应的“惩罚”，距边界越近，惩罚越大，在边界上给以无穷大的惩罚，从而保证迭代点一直在容许集内部移动，也就保证了约束条件的作用。构造如下的增广目标函数就可以实现上述想法：

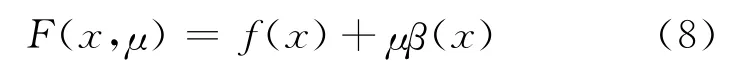
图2 计算流程图

4 算例及结论

根据以上方法，笔者编制了计算机程序，设计简单算例如图3以验证方法在理论上的正确性。为简单起见，优化计算时用式（3）计算目标函数值，用响应面方法拟合目标函数表达式，并且未严格按照规范要求约束最大坡度和坡度差，只对最大坡度和坡度差作了简单约束。计算结果表明，优化后的线路变坡点基本与地面点重合，目标函数值接近于0，优化结果令人满意。本文方法的正确性在理论上得到验证。

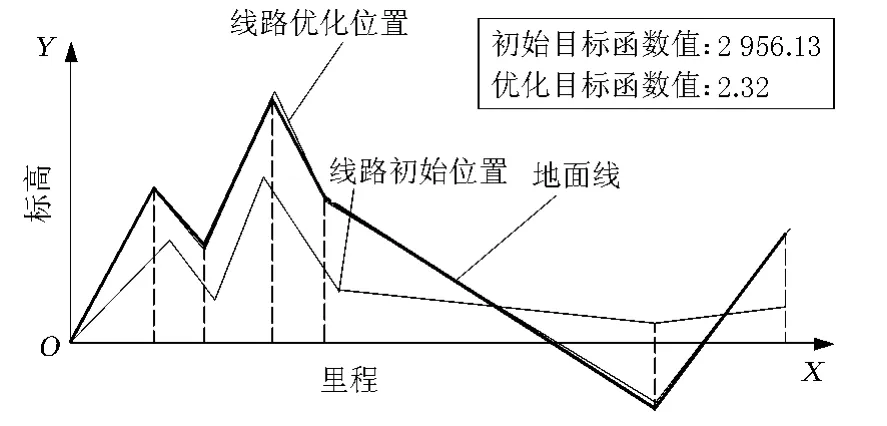
图3 算例

作为工程应用，笔者将本文方法用于某铁路纵断面优化计算，线路起始里程CK9＋900，终止里程CK32＋600，全长22.7km，共设桥梁1座，隧道4座，地面地形点最大高程差79.1m。人工设计线路纵断面变坡点个数22个，为了增加优化效果，将全部线路分成4段计算：第一段CK9＋900～CK15＋300，线路长度5.4km；第二段CK15＋300～CK20＋700，线路长度5.4km；第三段CK20＋700～CK28＋100，线路长度7.4 km；第四段CK28＋100～CK32＋600，线路长度4.5km。纵断面优化结果见表1，计算中目标函数收敛趋势见图4。经过优化计算，各坡段的目标函数值都有明显减小，变坡点在纵向和竖向都发生位移，线路纵断面更趋合理。限于篇幅，此处无法给出优化前后的纵断面对比图。经粗略估算，可节约工程费用约6%。

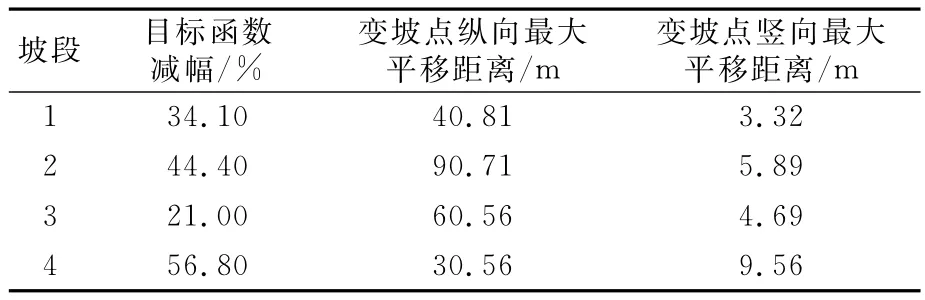
表1 纵断面优化结果

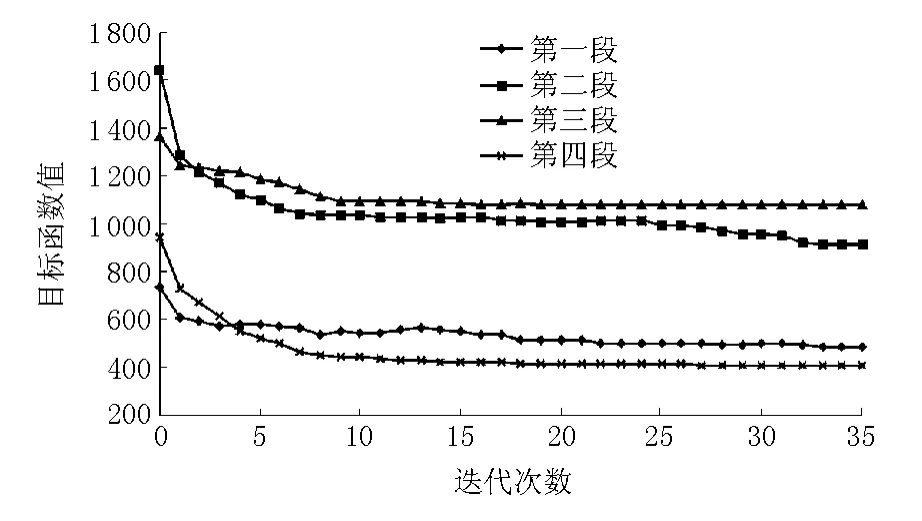
图4 目标函数值－迭代次数关系曲线

铁路纵断面优化是一项涉及面很广的综合性技术，需要各相关学科理论知识的相互协调配合。本文应用响应面方法拟合目标函数显式表达式，对铁路纵断面进行优化，理论计算和工程实际算例均表明了该方法的正确性和有效性。

［1］詹振炎.铁路选线设计的现代理论和方法［M］.北京：中国铁道出版社，2001.

［2］薛嘉庆.最优化原理与方法［M］.北京：冶金工业出版社，1992.

［3］GB50090－2006铁路线路设计规范［S］.北京：中国铁道出版社，2006.

［4］佟晓利，赵国藩.一种与结构可靠度分析几何法相结合的响应面方法［J］.土木工程学报，1997，30（4）：51－57.