高超声速滑翔式飞行器摆动突防设计

罗 畅，黄长强，丁达理，国海峰

(空军工程大学航空航天工程学院，西安 710038)

0 引言

高超声速滑翔式飞行器(Hypersonic Glide Vehicle，HGV)可利用自身特殊的气动外形提供升力在临近空间进行马赫数大于5的无动力滑翔飞行，其特点是飞行速度快、突防概率高、毁伤威力大、作战效能高。但随着拦截技术的发展，导弹防御系统正逐步发展成为包括助推段、中段和末段三层防御并实行地基、海基、空基、天基拦截相结合的全方位拦截系统。其中，地基中段防御系统最为成熟。高超声速滑翔式飞行器巡航飞行段弹道较为平缓，容易被拦截［1-4］。针对导弹防御系统的特点，设计HGV在巡航段的机动突防方法将成为突破导弹防御系统，实现精确打击远程目标的有效途径。

多约束条件下的高超声速滑翔式飞行器弹道优化问题一直是国内外研究的热点。大多数文献在研究突防弹道时，将飞行器看作质点，以燃油最省、航程最短，吸热量最小等指标作为优化目标，利用遗传算法、蚁群算法、Voronoi图等方法，在规避雷达探测范围的条件下达到优化弹道的目的［5-8］。文献［9］实现了一种摆动式机动的方法，但并未将其运用于突防弹道设计。

本文针对导弹防御系统中段拦截的特点，将HGV的横向机动过程与地基雷达的探测概率相结合，设计了一种摆动式机动突防方法。该方法解算得到的突防弹道使HGV在满足威胁时间窗要求的前提下毁伤概率的极大值取极小，取得了较好的突防效果。

1 系统模型的建立

1.1 导弹防御系统的简化模型

导弹防御系统主要由反导弹/飞行器武器，监视与跟踪系统，战斗管理和指挥、控制、通信和情报(BM/C3I)系统组成(见图1)。其中:监视与跟踪系统负责探测和发现来袭导弹/飞行器，并追踪其飞行轨迹;拦截器用于识别并拦截摧毁来袭导弹/飞行器;战斗管理和指挥、控制、通信和情报(BM/C3I)系统则负责控制整个导弹防御系统的操作［3-4］。

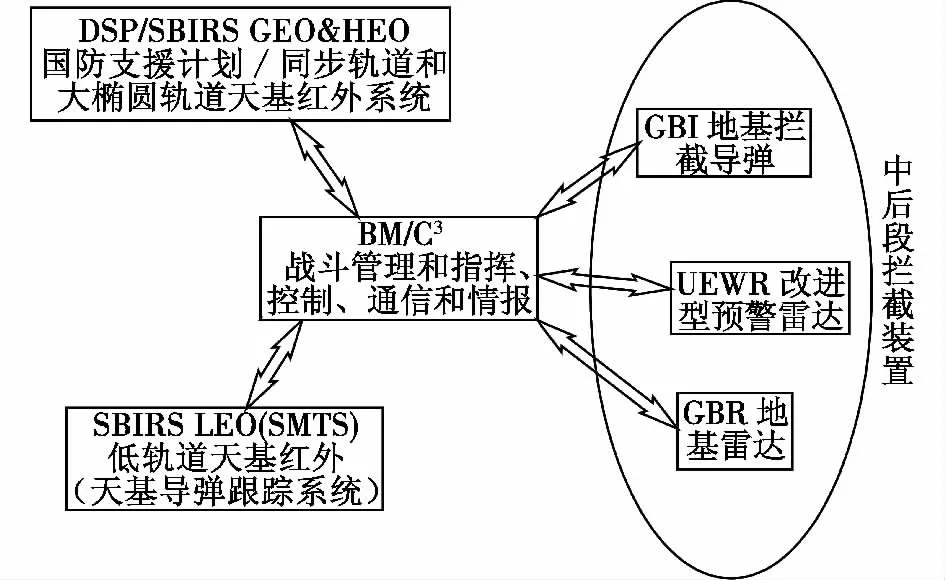
图1 导弹防御系统的组成结构示意图Fig.1 Configuration of missile defence system

导弹防御系统是一个可以进行助推段、末助推段和中后段拦截的反导防御系统。助推段和末助推段拦截层由天基动能拦截弹和部署在地球同步轨道上的监视与跟踪卫星探测器组成，中后段拦截层由地基动能拦截弹和地基探测器组成。因此，针对高超声速滑翔飞行器巡航段突防则主要考虑预警雷达、地基雷达和地基拦截导弹的影响。

设n为飞行区域内地基雷达总数，第i个地基雷达成功跟踪到飞行器的概率为Pti，则Pti可近似表示为

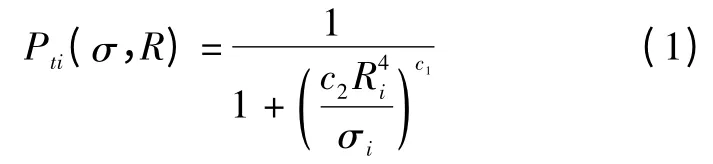
式中:Ri为雷达探测跟踪距离;σi为飞行器的雷达散射面积(RCS);c1、c2为雷达性能常数。

对于多个地基雷达，因为各雷达噪声以热噪声为主且各雷达探测跟踪时多工作于不同时间段，使用不同频率，所以可假设各雷达间没有相互作用。总的探测跟踪概率可表示为

式中，n为飞行区域内地基雷达总数。

1.2 高超声速滑翔式飞行器巡航段模型

在接近目标区域的巡航飞行段，高超声速滑翔式飞行器弹道较为平缓，假设其作等高度飞行，则运动方程可简单描述为

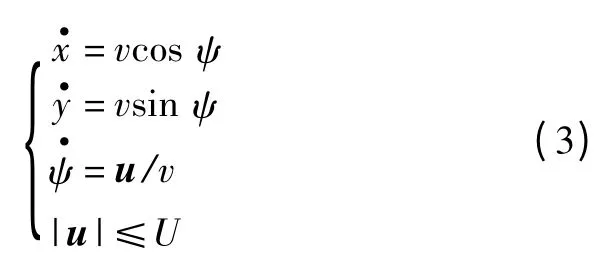
式中:x，y表征飞行器的位置;飞行器以速度v飞行，航向偏角为ψ;横向加速度为u;最大横向加速度不可超过U。HGV巡航段运动学量关系图如图2所示。

图2 HGV巡航段运动学量关系图Fig.2 Kinematic relation of cruising HGV

图2中，θ=arctan(y/x)，λ=θ-ψ+π。雷达与飞行器间目标线仰角φ、飞行器倾侧角ν，计算为

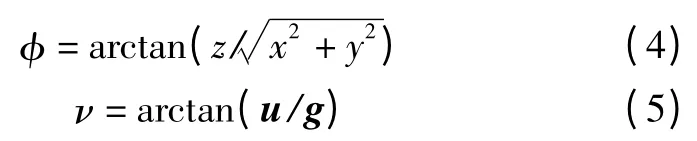
式中:z表示飞行器高度;g为重力加速度。

HGV的雷达散射面积与其相对于雷达的视线角以及倾侧角相关［10］，如图3所示。

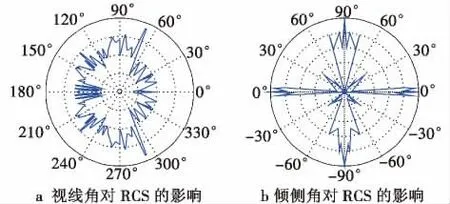
图3 影响RCS的相关因素Fig.3 Related factors of RCS

HGV头部及尾部RCS较小，两侧、背部及腹部RCS较大。因此可以使HGV在突防过程中做适当的机动，减小其RCS以达到减小其被地基雷达探测到的概率的目的。

本文在计算HGV的RCS时将其等效为一个椭球体。给出RCS近似表达式

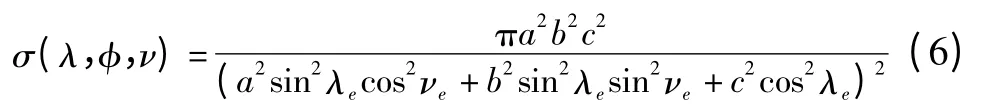
式中，λe=arccos［cosφ cosλ］;νe=ν-arctan［tanφ/sinλ］;a，b，c分别为椭球体3个方向的半轴长度。

1.3 毁伤概率模型

设HGV在整个突防过程中的存活概率为Ps，则Ps=1-PhPk/h。其中:Ph为HGV被击中的概率;Pk/h为HGV被击中条件下毁伤的概率。

本文中假设Pk/h=1，所以HGV被毁伤的概率可表示为

在不考虑其他因素的条件下，Pk的上限即为HGV被地基雷达探测到的概率Pt。减小Pt的值即可达到降低毁伤概率、提高存活概率的目的。

2 基于威胁时间窗的摆动式机动突防弹道设计

2.1 摆动式机动突防的实现

摆动式机动的实现问题可以简单描述为:根据所需摆动式机动弹道的关键参数(一般为机动幅值和机动频率)求解迎角、倾侧角等控制量。前提是要保持飞行器在纵向平面的稳定性并且满足动压、过载以及气动加热等约束条件。

设飞行器机动起始、终止位置分别为:A(x0，y0，z0)，B(xf，yf，zf)。建立坐标系Oxyz，其中:z轴沿地心矢方向，向上为正;x轴与z轴垂直，指向机动终止位置B;y轴与x轴和z轴构成右手坐标系。

摆动式机动如图4所示。

图4 摆动式机动示意图Fig.4 Lateral weaving maneuver

摆动式机动弹道可以有多种形式。以按正弦规律变化为例，如图4所示，侧向机动距离可表示为

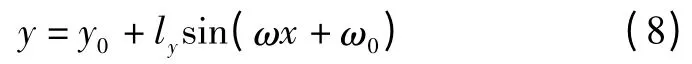
式中:y0为初始值;ω为机动频率;ly为机动幅值;ω0为初始相位角;x为当前位置在x轴方向上的大小。本文中令y0、ω0均为0。

假设速度矢量偏离xOz平面的角度为小量，则

式中:v为飞行器速度大小;D为飞行器所受阻力大小。

对式(8)求关于时间的二次微分得到y轴方向的横向过载

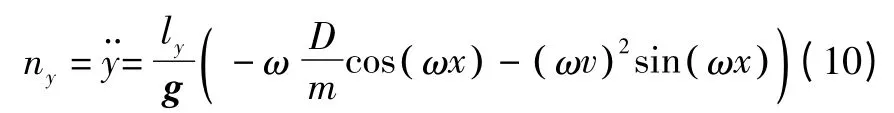
令L为飞行器升力大小，ν为倾侧角，根据倾侧角定义

至此，飞行器倾侧角以及横向过载均与x轴方向上的飞行距离联系起来。

为保持飞行器在纵向平面的稳定性，需要调整迎角以抵消由于侧向机动所带来的升力变化(L变为L cosν)。设地心距为r，此时倾侧角应满足

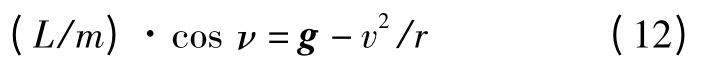
结合式(11)可知倾侧角的变化规律为

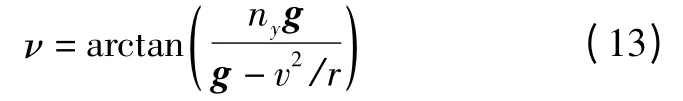
为使摆动式机动满足动压、过载以及气动加热等约束条件，则需根据各约束条件所允许的上限值解算出相应的迎角-速度飞行走廊［9］，确定迎角取值。

2.2 威胁时间窗

在地基拦截导弹发射之前，地基雷达需要时间Tresp跟踪并锁定目标。拦截导弹发射后，在其飞行时间段Tfo，地基雷达仍然需要持续跟踪目标。Tresp取决于雷达的性能，Tfo则由拦截导弹的速度vm和两者的相对距离Ri决定:Tfoi=Ri/vm;Tfo=mii n Tfoi。

定义威胁时间窗T=Tresp+Tfo。如果在威胁时间窗内，地基雷达丢失了目标，则必须重新跟踪并发射地基拦截导弹。那么，地基拦截导弹要在时间点t成功毁伤HGV，地基雷达则必须在时间段［t-T，t］内对HGV保持持续跟踪状态。本文中将T视为一常量。

突防过程的流程如图5所示。

图5 突防过程流程图Fig.5 Flow chart of penetration

在突防的整个过程中，HGV将经历多个威胁时间窗，而要达到成功突防的目的则要求在每个威胁时间窗内毁伤概率尽可能小。

假设HGV经历的威胁时间窗总数为m，第i个威胁时间窗内毁伤概率的上限表示为

式中，u为飞行器横向加速度，作为控制量隐含于Pt中。

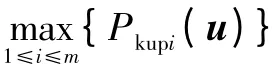
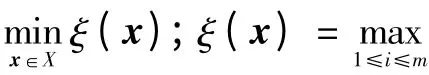
目标函数的一个主要特征是，即使每个fi(x)都具有连续偏导数，目标函数在使两个以上的函数等于ξ(x)的那些点处往往不可微。因此Minimax问题属于不可微优化。

本文所研究的内容属于带约束的非线性Minimax问题，用公式表述为

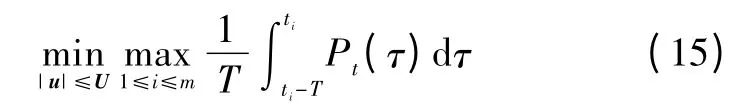
由式(1)做Pt与R、σ的关系图如6～图7所示。

图6 探测概率与探测距离的关系Fig.6 Relationship of explorative probability and distance

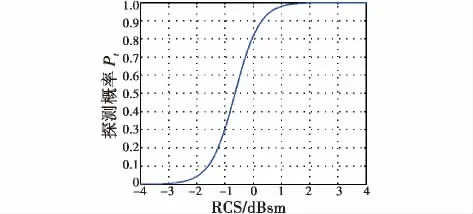
图7 探测概率与飞行器RCS的关系Fig.7 Relationship of explorative probability and RCS

图6、图7证实了HGV在威胁时间窗内做摆动式机动的可行性。在探测距离一定的条件下HGV的RCS对地基雷达探测概率有显著的影响。因此，在短时间内可以利用HGV的机动飞行来控制其RCS大小，降低其被地基雷达探测跟踪到的概率以实现较好的突防效果。

3 仿真分析

3.1 HGV突防单个地基雷达

假设地基雷达处于位置O(0 km，0 km)，最大探测距离为150 km。HGV初始位置位于A(-150 km，-150 km)，目标点位于B(150 km，150 km)。HGV的最大横向加速度|U|=5g，初始航向偏角为ψ0=π/6，巡航高度为25 km，巡航马赫数为8，巡航总时间TM≤3 min。利用时间窗理论设计突防弹道，设威胁时间窗T=12 s，仿真结果如图8～图9所示。

图8 以航向偏角为自变量设计的突防弹道Fig.8 Trajectory of penetration based on heading angle

图9 结合飞行器横向机动设计的突防弹道Fig.9 Trajectory of penetration based on lateral maneuver

由图8所示的突防弹道解算得到HGV被探测到的概率的极大值P1kup(u)为0.9871。由图9所示的机动突防弹道解算得到HGV被探测到的概率的极大值P2kup(u)为0.1651。图8中仅仅是以改变航向偏角的方式使Pkup(u)达到最小，并没有考虑到HGV的RCS对探测概率的影响，整个突防过程中飞行器倾侧角ν为0。图9中将HGV被探测到的概率通过其RCS与飞行器的横向机动联系起来，通过改变横向加速度u来改变倾侧角ν和视线角λ，得到了较好的突防效果。两种突防弹道的对比图如图10所示。

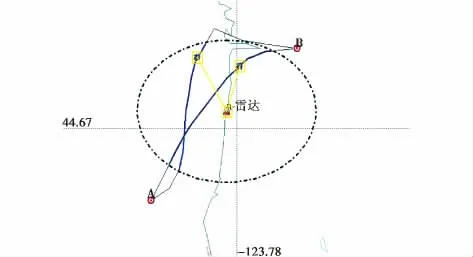
图10 两种突防弹道的对比图Fig.10 Contrast of two trajectories

对两种突防弹道的运动学参数进行比较，如图11～图14所示。

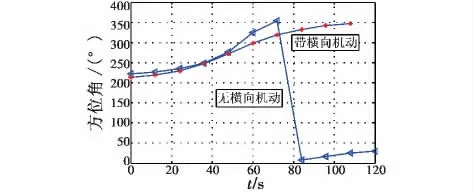
图11 方位角对比图Fig.11 Contrast of aspect angle

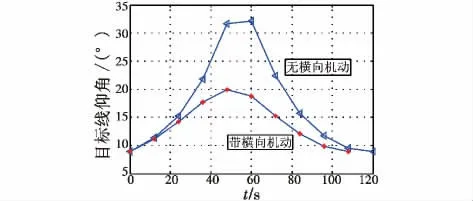
图12 仰角对比图Fig.12 Contrast of elevation angle

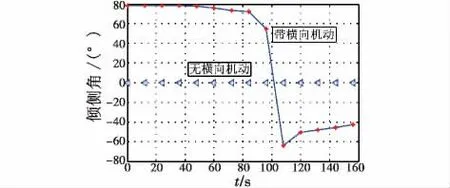
图13 倾侧角对比图Fig.13 Contrast of bank angle

图14 距离对比图Fig.14 Contrast of distance

由图3、图11～图14可知，虽然两种突防弹道与地基雷达之间的距离并无较大的差异，但相对于不考虑横向机动的情况，经极大极小值原理设计的机动突防弹道中HGV的RCS很小且暴露时间很短，使得P2kup(u)取值仅为0.1651，从而达到了预期的突防效果。由两种突防弹道得到各性能参数如表1所示。

表1 两种突防弹道性能参数Table 1 Parameters of two trajectories

所设计的摆动式机动突防弹道中，飞行器以较大的航时和航程换取了较小的毁伤概率和较大的存活概率。

3.2 HGV突防多个地基雷达

假设有两台地基雷达，最大探测距离均为150 km。两者独立工作，分别处于位置O1(0 km，0 km)、O2(0 km，200 km)。HGV的最大横向加速度|U|=5g，初始位置位于A(-200 km，0 km)，目标点位于B(200 km，200 km)。HGV初始航向偏角为ψ0=π/6，于25 km高度巡航，巡航马赫数保持为8，巡航总时间TM≤5 min。

以j∈{1，2}编号两台地基雷达，则飞行威胁时间窗可表述为

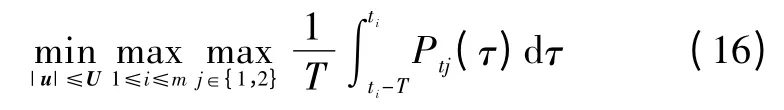
式中，Ptj表示HGV被第j台地基雷达探测到的概率。取T=12 s，仿真结果如图15～图16所示。

图15 结合飞行器横向机动设计的突防弹道Fig.15 Trajectory of penetration based on lateral maneuver

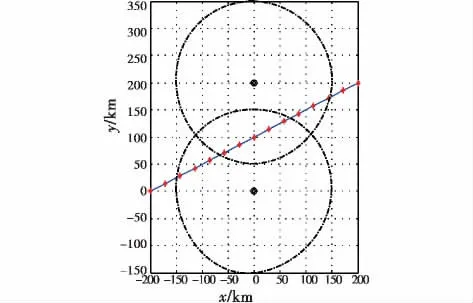
图16 以航向偏角为自变量设计的突防弹道Fig.16 Trajectory of penetration based on heading angle

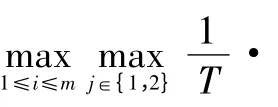
4 结论

本文利用导弹防御系统威胁时间窗将HGV、地基雷达和拦截导弹联系起来加以考虑，建立毁伤概率模型，并认为提升HGV生存概率的关键在于毁伤概率最大的威胁时间窗。在实现HGV摆动式机动的前提下实时改变HGV的RCS以使毁伤概率在所有威胁时间窗内的极大值极小化。仿真分析表明，所设计的机动突防弹道取得了较好的突防效果，使HGV的生存能力得到提高。

［1］雍恩米.高超声速滑翔式再入飞行器轨迹优化与指导方法研究［D］.长沙:国防科学技术大学，2008.

［2］陈小庆，侯中喜，刘建霞.高超声速滑翔飞行器弹道特性分析［J］.导弹与航天运载技术，2011(2):5-9.

［3］刘兴.防空防天信息系统及其一体化技术［M］.北京:国防工业出版社，2009.

［4］孙连山，杨晋辉.导弹防御系统［M］.北京:航空工业出版社，2004.

［5］STARKEY R，RANKINS F，PINES D.Coupled waverider/trajectory optimization for hypersonic cruise［C］//The 43rd AIAA Aerospace Sciences Meeting and Exhibit 10-13 January 2005，Reno，Nevada，10.2514/6.2005-530.

［6］CHUANGCH，MORIMOTOH.Optimal periodic cruise for a hypersonic vehicle with constraints［C］//AIAA Guidance，Navigation and Control Conference，San Diego，CA，29-31 July，1996.10.2514/6.1996-3876.

［7］GRANT M J，CLARK I G，BRAUN R D.Rapid simultaneous hypersonic aerodynamic and trajectory optimization using variational methods［C］//AIAA Atmospheric Flight Mechanics Conference，Portland，Oregon，08-11 August，2011，10.2514/6.2011-6640.

［8］SZCZERBA R J.Robust algorithm for real-time route planning［J］.IEEE Transactions on Aerospace and Electronic Systems，2000，36(3):869-878.

［9］谢愈，刘鲁华，汤国建，等.高超声速滑翔飞行器摆动式机动突防弹道设计［J］.航空学报，2011，32(12):2174-2181.

［10］王若鹏.极大极小问题的数值解法［D］.西安:西北大学，2002.