基于思维导图的数学题解后反思及启示

☉江苏省常熟市海虞中学 张文明

基于思维导图的数学题解后反思及启示

☉江苏省常熟市海虞中学 张文明

*本文系江苏省十二五重点立项课题“基于思维导图的高效法的实践研究”(课题编号：B-b/2 0 1 1/0 2/0 0 7；主持人：韩建光)及子课题“关于初中生运用思维导图进行学后总结的实践研究”(主持人：朱仁红)的研究成果之一.

在学习数学的过程中，“理解”无疑是第一位的［1］.这就要求学生在学习后及时总结反思以减少被动性、滞后性、无序性、盲目性和低效性，提高自觉构建知识网络的意识，从而使知识序列条理化、系统化.思维导图正是帮助学生学后反思以理清思维秩序、增进程序性理解的有效工具.

一、思维导图

思维导图是英国“记忆之父”托尼·巴赞（Tony Buzan）开发出来的一种组织性思维工具，是从一个中心主题发散出来的自然结构，通过符号、关键词、图像、线条和颜色，遵循一套基本、简单、自然易被大脑接受的规则，逐步建立一个有序的发散的树状图，它是对思维过程的导向和记录［2］.这是一种将放射性思考具体化的方法，放射性思考是人类大脑的自然思考方式，以大脑中的某一个知识点为思维中心，从这个知识点出发引发出与之相关的其他知识点，这些知识点又可以成为另外的思维中心.这种发散性的结构符合大脑工作的原理，体现了人们思维过程中的多向性和跳跃性，是一种能够帮助人们分析问题、整理思路、快速学习的方法和工具.

思维导图具有使“单调的知识形象化，抽象的知识具体化，零碎的知识系统化，复杂的知识简单化，隐性的知识显性化［3］”等特点，因此在数学学习活动中，思维导图有助于学生对数学知识的综合理解.

二、解后反思案例

例题 如图1，C为线段AE上一动点（不与点A、E重合），在AE同侧分别作正△ABC和正△CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连接PQ.试判断△CPQ的形状.

分析：由题设易求∠PCQ=60°，观察图形，感知猜测△CPQ是一个等边三角形.现在有两个思路可以选择：一是推理出∠PQC=60°（或∠QPC=60°），从而得到∠PCQ=∠PQC=∠QPC，根据“三个角相等的三角形是等边三角形”证得猜测成立；二是推理出CP=CQ（或CP=PQ或CQ=PQ），根据“有一个角是60°的等腰三角形是等边三角形”证得猜测成立.

解：因为△ABC和△CDE都是正三角形，

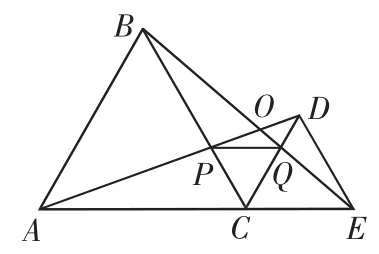
图1

所以△CPQ是等边三角形.

1.解后反思

由于授课班级学生已经有了使用思维导图进行解后反思的基础与实践，因此不少学生都用思维导图进行了解后反思.

2.反思解题过程

在解后反思环节的师生交流中，一些学生采取的思路是列示意图，然后对解题思路进行甄别与整合，其实质是分析法，解题思路如下.

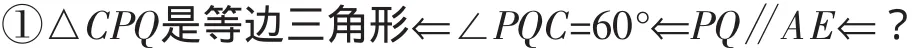
所以这条思路不便推理出猜想.

所以这条思路是可行的.

薛同学所画的思维导图如图2所示.

图2

3.反思问题涉及的基础知识

问题中涉及的基础知识有全等三角形的性质、全等三角形的判定、等边三角形的性质、等边三角形的判定等知识.学生需从复杂图形中识别基本图形，排除干扰，从而获得有效信息，进行正确推理.同时，由于本题结论并未给出，需要学生先观察、操作，猜想结论（甚至在这个环节还有几位学生采用了度量边或角来猜测△CPQ的形状），再进一步演绎推理.学生在反思中基本能够发现问题所涉及的基础知识，图3即是一份较好的对基础知识进行反思的思维导图.

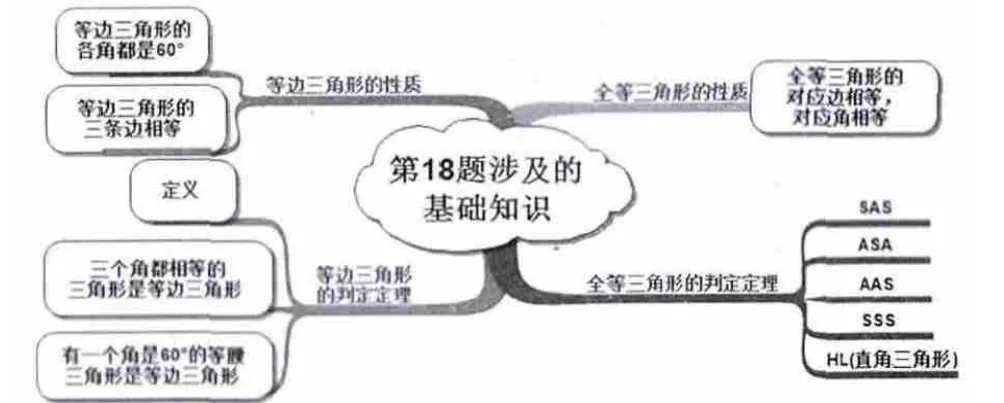
图3

4.反思解题思想

本题结论未直接明确告知，且难以一步达成结论（△CPQ是等边三角形），所以既要先猜测，又要进行证明，故采用分析法较为合理.当思维比较顺畅时，解题适宜按照由因导果的顺序使用综合法；当思维遇阻时，则解题适宜执果索因，分析法就会大显身手.而对于一般的数学问题，我们可以从一般解题步骤、常用解题方法、基本数学思想、解题元认知策略等方面进行反思（如图4）.

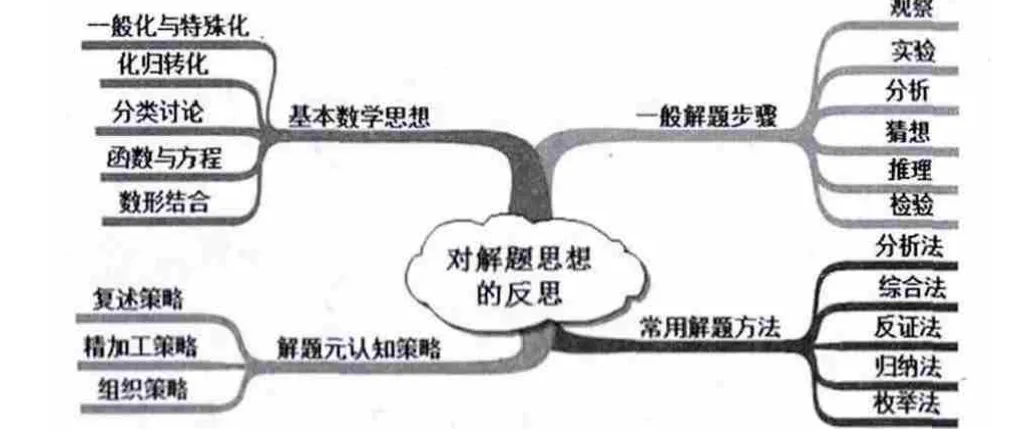
图4

5.反思问题的拓展与归类

对于本问题，如果能够有“脚手架”，学生更容易顺利完成，因此学生对此进行了思维导图式反思.该生还提出了一些拓展性问题，并对问题的架构进行了解构与重组（如图5）.

图5

由上述典型的思维导图可观察出学生的“图式”思路，学生的反思基本是围绕基础知识、基本技能、基本数学思想方法、基本的数学活动经验等方面进行的，这正是《义务教育阶段数学课程标准（2011年版）》与《义务教育阶段数学课程标准（实验版）》的较大区别之一.具体反思内容可综合为如图6所示的思维导图.

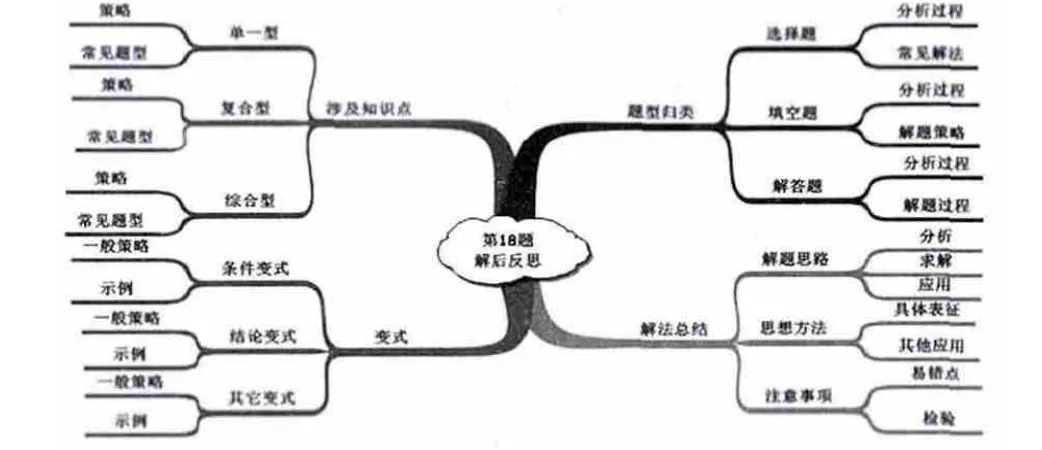
图6

三、思考与启示

1.基于思维导图的解后反思调动了学生学习的积极性

课程标准实施后，学生的主体性地位得到明确，但是在数学学习活动中仍然存在为数不少的学生对教师具有极强的依赖性.这部分学生等着教师总结知识模块、总结规律，然后记笔记.这种被动的学习方式既抑制了学生的主体创造性，又降低了学习效率.归根到底，是由于学生的积极性不够造成.而思维导图的图式化表示既有规则要求，又允许有个性化发挥，这扩大了学生的自我发挥空间，学生的积极性大有提高，从而切实提高了数学学习的有效性.

2.基于思维导图的解后反思呈现了知识系统的直观化

学生的思维过程是抽象的，思维导图的图式化直观地表现了学生的思维过程，从而使得隐性知识显性化.这样的直观化、可视化的思维过程有助于学生对问题表征、问题变式进行思考和理解，从而达到举一反三的功效.从某种意义上说，思维导图式的解后反思与“数形结合”的数学思想具有异曲同工之妙.

3.基于思维导图的解后反思建构了知识系统的网络化

由于课堂时间的限制，每一次数学活动中学生所收获的知识点总是相对孤立和分散的，学生难以从整本书甚至整个学段（比如初中三年或者中学六年）上把握整个知识脉络，从而难以建构出相对完整的知识网络.这也是有些学生每节课的练习都做的不错，但是一遇到综合问题就不知所措的原因之一.基于思维导图的解后反思恰好有效弥补了这个空缺，使得整个知识体系在多次的图式化表示中得以趋近系统化、网络化.

四、结束语

反思是数学思维的核心和动力［4］，而基于思维导图的解后反思顺应了大脑的自然思维模式，引领学生从题目的分析与架构、解题方法、相关变式等方面进行发散性思考，使得学生的知识建构具有“随风潜入夜”的自然与平适.这种反思方式不仅提升了学生学习数学的兴趣，也提高了数学学习的效率，使得学生在思考和表达中深化了对数学知识体系的表征与理解.

1.马复.试论数学理解的两种类型——从R.斯根普的工作谈起［J］.数学教育学报，2001（3）.

2.［英］托尼·巴赞.思维导图：大脑使用说明书［M］.张鼎昆，徐克茹，译.北京：外语教学与研究出版社，2005.

3.吴丹，丁青.思维导图在英语听说教学中的应用与探索［J］.外语周刊，2012（81）.

4.杨绍平.反刍数学中考，思索数学教学——一道中考试题引发的思考［J］.中学数学（下），2013（11）.