水力旋流器的三维模拟

刘建平，陈茂兵

（中建中环工程有限公司，江苏 南京 210008）

1 引言

水力旋流器作为一种机械式的分离装置广泛应用于采矿、化工、食品、环保、医药等各个行业。它的主要原理是利用工作介质的密度差异，所受的离心力不同，形成溢流与底流的分层，从而使混合的工作介质分离开来。计算流体力学（CFD）是通过对物理模型划分网格，离散封闭的湍流模型，然后进行迭代计算的一种流体力学的数值计算方法。旋流器作为一种结构复杂、含有强旋流的湍流流动，利用计算流体力学来研究、设计和改进这种设备一直是国内外研究人员的一个方向。如Dai等采用k－ε湍流模型对旋流器内流场进行了数值模拟[1]，He等在k－ε模型中引入Richardson数来修正湍动能耗散率，从而考虑了旋流器内由于强旋运动而造成的各向异性问题[2]；邹宽等利用雷诺应力模型分析旋流器内流场分布，得到了与试验数据比较接近的结果[3]。

雷诺应力模型（RSM）在模型化雷诺应力张量时，对于非同向雷诺应力张量的乘积并没有如标准k－ε两方程模型一样设为0，而是通过一系列变换和假设建立方程将整个模型封闭，因此虽然雷诺应力模型要比标准k－ε两方程模型的方程多，但是由于考虑了湍流的各向异性，它是现有湍流模型中比较适合应用于旋流器数值模拟的。文献[3]中邹宽等利用RSM模型计算旋流器流场，得到了较好的结果，但是他采用了简化的二维轴对称的物理模型，而实际旋流器单向入口非对称的结构肯定会对内部流场产生重大影响。因此本文就是采用RSM模型，对文献[3]中的旋流器进行三维数值模拟计算，得到的结果与实验数据及文献[3]中的计算数据进行比较，分析非对称结构对旋流器流场的影响。

2 物理模型

本文的物理模型采用文献[3]中的旋流器：旋流器直径D＝76mm；溢流口直径D1＝0.34 D；底流口直径D2＝0.16 D；进口采用方形进口，边长根据雷诺相似准则得到α＝0.07πD；溢流管壁厚3mm；柱段长度L1＝0.67 D；锥段长度 L2＝4.33 D；溢流管插入深度L3＝0.4 D；工作介质为水，进口流量为0.407kg／s；分流比1∶4（底流／溢流）；其他边界条件根据经验公式得到。物理模型的计算网格数为87万网格（图1）。

图1 水力旋流器物理模型

3 计算结果

首先取距离顶部0.18m距离处分析，与试验数据和文献[3]的计算结果比较如下。

从图2和图3中我们可以看出，对于轴向速度，三维模拟计算的结果在峰值部分要更接近实验值，在轴心位置也是如此。而对于r＞0.01m的部分，无论是切向速度还是轴向速度，三维模拟结果与实测值吻合得都相当好。这说明采用三维数值计算的结果是可信的。

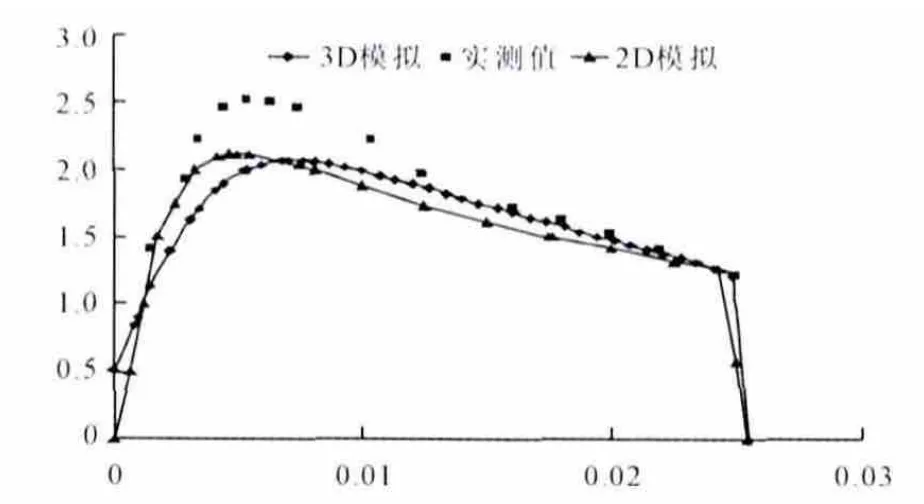
图2 0.18m处截面上的切向速度

图3 0.18m处截面上的轴向速度

图4是距离顶部0.06m、0.18m、0.37m处圆截面上4个半径上的切向速度。

图4 0.06m、0.18m、0.37m处截面上4个方向的切向速度

从图4中我们可以看出，z＝－0.18m处，4个方向的切向速度比较一致，但是在z＝－0.06m处和z＝－0.37m处，切向速度有比较明显的差异，这是因为在z＝－0.18m处，流场已经充分发展，对称形状的圆柱段和圆锥段结构使得流场更接近于轴对称；在z＝－0.06 m处，非对称结构的单向入口对流场影响还比较大，因此流场呈现非对称的形态；而在z＝－0.37m处，流场接近出口，流场的对称形态被破坏，各个方向的切向速度再次呈现较大的差异。另外值得注意的是在轴心处，各个高度的切向速度都不为零，这和轴对称假设是完全矛盾的。

4 结论

通过分析三维模拟计算的结果，我们可以得到如下结论。

（1）通过三维数值计算来模拟旋流器的流场具有一定的可信性，这为产品的开发和改进提供了一种可行的选择；

（2）对于单向入口非对称结构的旋流器，利用二维轴对称模型来进行数值计算是值得商榷的，因为非对称结构对流场具有较大的影响。

[1]Dai G，Li J M，Chen W M.Numerical Prediction ofthe Liquid Flow Within a Hydrocyclone[J].Chemical Engineering Journal，1999，74：217～223.

[2]He P，Salcudean M，Gartshore I S.A Numerical Simula－tion of Hydrocyclones[J].＇I1ans .IchemE，1999，77（Part A）：429～439.

[3]邹 宽，杨 茉，曹 玮，等.水力旋流器湍流流动的数值模拟[J].工程热物理学报，2004（1）：127～129.