S3PR网的一种最大许可活性监督控制器设计方法
闫明明,赵 咪
(1.电子科技大学机电工程学院,四川 成都 610054;2.石河子大学机械电气工程学院,新疆 石河子 832003)
0 引言
死锁是对柔性制造系统(Flexible Manufacturing Systems,FMS)进行控制设计时必须考虑和解决的问题,实现优化的无死锁的FMS是目前工程设计者面临的主要课题之一。并行FMS共享有限的资源,资源的不合理分配可能造成死锁,降低系统的生产效率,甚至造成重大的经济损失和灾难性后果。Petri网能够模拟离散事件系统的并发和冲突行为,并能反映系统的动态特性,非常适合复杂的并行FMS这种异步并发系统的建模、分析、控制和调度。通过对Petri网模型实施添加控制库所及其连接弧等有效的系统设计,可以限制系统对资源的申请,达到阻止死锁的目的[1-5]。受控网系统可达状态的多少是评价Petri网控制器的一个重要指标。一个Petri网系统的可达状态按标志描述可以划分为死锁标志、坏标志、危险标志和活标志四类[6-8]。对网系统进行控制设计的目的是去除死锁标志和坏标志,即禁止标志,尽可能保留活标志和危险标志,即可保留标志。可以通过限制系统对资源的申请,保证所有的禁止状态不可达,保留系统中的所有可达状态[9]。
在Petri网的死锁分析方法中,基于可达图分析和结构分析的方法占主要地位。基于可达图分析的区域理论[2]可以获得Petri网的最大许可控制器,但是该算法在具体实施时要产生网的可达图,计算量巨大,甚至会出现状态爆炸问题。基于结构分析的死锁预防策略对Petri网模型中的严格极小信标添加控制库所,使其不被清空,从而使受控网无死锁或者活。然而现有的大部分信标控制策略添加控制库所的方式对系统的约束过大,使得受控网的可达状态无法达到最大许可数目。Piroddi等[5]基于信标理论提出一种次最优的死锁控制策略;Li和Zhou等[10]给出一种基于信标和区域理论的最大许可死锁控制策略,改善了单独用区域理论求解最优控制器的计算复杂度。
本文针对Petri网的一个子类拥有资源的简单加 工 进 程 系 统 (System of Simple Sequential Process with Resources,S3PR)网提出一种基于结构分析的死锁控制策略,若施加该策略后的活性Petri网控制器存在,则可以保证受控网具有最大许可行为。首先对原S3PR网系统的信标进行分析,获得一组标志向量M表示的低于某个上限的广义互斥约束集合,使信标的标志数不超过某个上限值,并添加控制库所及相应的连接弧,若受控网是活网,则具有最大许可行为;否则,采用迭代方法对可能出现的所有可清空严格极小信标添加基于广义互斥约束的控制器,使系统的所有禁止状态不可达,即将网系统的所有可达状态限制为可保留状态。本策略将基于信标的死锁预防控制策略转化为禁止状态监控问题,因为算法有可能涉及到迭代,所以对可达状态性能要求比较高的、结构相对简单的网模型按本文策略进行控制,若施加控制后的受控网是活的,则可以得到最大许可Petri网控制器。
1 Petri网中的基本定义及性质[1,3-4,11]
Petri网是一种高效的图形化的研究离散事件动态系统的建模工具,它的一些基本定义及性质如下所示。
定义1 令N=(P,T,F)是一个Petri网系统,M0是网N的初始标志。一个广义互斥约束(Generalized Mutual Exclusion Contraints,GMEC)(l,b)定义了一个合法标志集合 Ml(l,b)={M∈IN|P|(lTM≤b},这里l:P→IN 表示加权向量,是一个从库所到非负整数集上的映射,且b∈IN+。其中‖l‖={p∈P|l(p)>0}是l的支撑,IN+={1,2,…}是正整数集合。
一个广义互斥约束可以表示为(l,b),或简写为l。
定义2 令N=(P,T,F)为一个Petri网系统,M0是网N的初始标志。一组广义互斥约束的集合(L,B),定义了一个合法标志集合Ml(L,B)=∩mMl
i=1(li,bi)={M∈(IN|P||LTM≤B},其中L=[l1|l2|…|lm],B=[b1,b2,…,bm]T。
一组广义互斥约束的集合可以表示为(L,B),或简写为L。
定义3 给定一个网系统(N,M0),N=(P,T,F,W),以及一个GMEC约束(l,b),对该约束添加控制库所V 后的网记为(NS,M0S),NS=(P∪V,T,FS,WS),则[CS](V,·)=-lT[C],M0S(V)=b-lTM0,且∀p∈P,[CS](p,·)= [C](p,·),M0S(p)=M0(p)。其中:[C]为网N 的关联矩阵,[CS]为添加控制库所后的关联矩阵。
定义3对Petri网的一个GMEC约束添加一个控制库所,该约束对应的禁止库所(权值非零的库所)多重集合和控制库所组成一个库所不变量,使得标志的加权和始终不超过该约束对应的上界,从而避免死锁状态。
性质1 令(N,M0),N=(P,T,F)是一个普通Petri网系统,如果网N中没有信标可能被清空,则称(N,M0)是无死锁的(deadlock-free)。
对Petri网的一些具体定义请参见文献 [1,11]。
2 死锁预防策略
这里的死锁预防策略是针对一类普通网S3PR网提出的。S3PR网的相关定义请参见文献 [1]。
性质2 一个拥有资源的简单加工进程系统S3PR,是k(k∈IN+)个拥有资源的简单加工进程(Simple Sequential Process with Resources,S2PR)通过共享资源PRi融合而成的Petri网,N=Oi=1kNi=(PS∪P0∪PR,T,F),k∈IN+,Ni=(Pi∪∪PRi,Ti,Fi),Ni表示第i个S2PR网。其中:①Pi≠∅,∉Pi;②=(Pi∪,Ti,Fi')为一强连通状态机,N'i是从网Ni中移走PRi后的网;③N′i中每一个回路都包含库所;④当任意两个N′i共享一组资源库所时,都是可组合的。
定义4 设N=Oi=1kNi=(P∪P0∪PR,T,F)是一个S3PR网系统,Ir为包含资源r的极小P-不变式,其中{r}=‖Ir‖∩PR,p0∉‖Ir‖,P∩‖Ir‖≠∅且Ir(r)=1,称H(r)=‖Ir‖\r为资源r的持有者。
定义5 设N=Oi=1kNi=(P∪P0∪PR,T,F)是一个S3PR网系统,S是网N的一个信标,其中S=SR∪SP,SR=S∩PR,SP=S\PR,SR表示信标S中的资源,SP表示信标S中的工序状态库所。将信标S的补集以多集的形式定义为[S]=r)\S。[S]代表需使用资源r但不属于信标S的库所的集合,该集合中的元素是造成信标S被清空的直接原因。
定义6 设(N,M0)是一个Petri网系统,S是网N 的一个信标。如果∀M∈R(N,M0),M(S)>0成立,则称S为可控信标。
对给定的S3PR网系统N=Oi=1kNi=(P∪P0∪PR,T,F),可以对系统中每个可清空严格极小信标添加一个控制库所,使其P-不变式可控,同时满足不等式

式中:M是网N的标志向量,ξS是信标S的控制深度变量,0<ξS<M0(S)。因为S∪[S]是网N 的一个P-不变式的支撑,且不变式支撑在任何状态下的托肯数总和保持不变,所以式(1)可以通过以下不等式的实现得到保证:
M([S])≤M0(S)-ξS。 (2)
由此可以得到如下定理:
定理1 设N=Oi=1kNi:=(P∪P0∪PR,T,F)是一个S3PR网。若S是N的一个信标,则当满足M([S])≤M0(S)-ξS或M(S)≤ξS时,信标S不会被清空。


由定理1知,通过对一个S3PR网系统中的所有可清空严格极小信标进行分析,可以得到一组类似(2)的GMEC集合,再采用定义3的方法添加相应的控制库所和连接弧,可以保证原S3PR网中的所有信标均不会被清空。但是这样一来,添加了控制库所的新网中可能会产生新的可清空信标,导致受控网仍有死锁状态存在的可能。为此,笔者进行了探索并设计了以下迭代控制算法,在网结构不太复杂的情况下,可以得到具有最大许可行为的Petri网控制器,即若添加控制器后的受控网是活的,则可以达到最大可达状态。
算法1 基于信标的死锁控制最大许可控制器设计算法。

步骤4 求出信标的补集集合Π*m,令Π*m:={[S1],[S2],…,[Sk]},k∈IN+。
步骤5 由信标补集集合Π*m得出状态向量表示的 GMEC集合(L,B):LM≤B,L=[l1|l2|…|lk],B=[b1,b2,…,bk]T。其中li为非零向量且li:= [Si],bi= M0(Si)-ξSi,ξSi:=1,i=1,2,…,k。
步骤6 根据定义3,对GMEC集合(L,B)添加控制库所集合{v}={v1,v2,…,vk},所得网记为(Nm′,Mm′)。
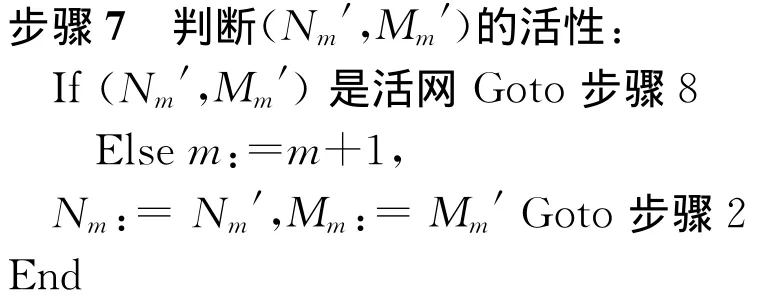
步骤8 Nm′= N′,Mm′= M0′。
步骤9 输出网(N′,M0′)。
定理2 按算法1所述的死锁预防策略对原网N 进行控制,受控网(N′,M0′)是一个ES3PR(system of extended simple sequential process with resources)网。
定理3 若算法1输出活性控制器,则该控制器具有最大许可行为。
证明 因为每一个信标的控制深度变量取值为1,所以添加的控制库所仅剔除了死锁标志和必然导致死锁的坏标志。因此,若算法1输出活的控制器,则该控制器具有最大许可行为。
Petri网中可达状态数目和可清空信标数目与网规模在理论上呈指数关系,即基于可达图分析方法和基于结构分析的信标方法两类控制策略都是指数复杂性的。因此,算法1关于网规模是指数复杂性的,算法1适用于对许可行为性能要求比较高、网规模不大、标志数偏多的S3PR网系统,若施加控制后的网为活网,则具有最大许可行为。
3 死锁控制柔性制造系统应用实例
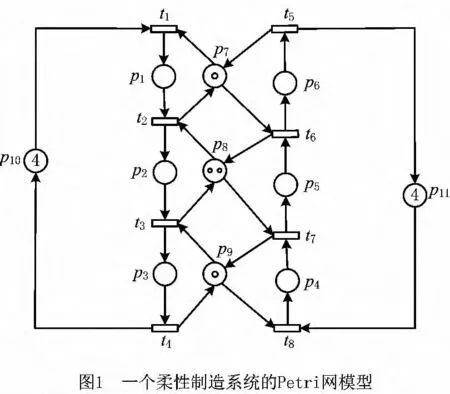
一个柔性制造系统(Flexible Manufacturing System,FMS)包括1台机床M1和2个机器人R1,R2,生产两种零件,其Petri网模型如图1所示,库所p7和p9用来表示机器人R1,R2,p8表示机床M1。该Petri网模型包含三个严格极小信标S1={p2,p6,p7,p8},S2={p3,p5,p8,p9},S3={p6,p7,p8,p9},它们的补集分别为[S1]=p1+p5,[S2]=p2+p4,[S3]=p1+p2+p4+p5。基于算法1得到图1所示网系统的一组GMEC:
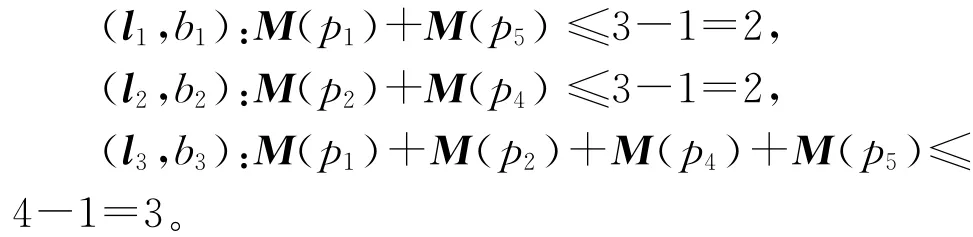
按照算法1添加3个控制库所{v1,v2,v3},控制库所的初始资源数和前、后置分别为:
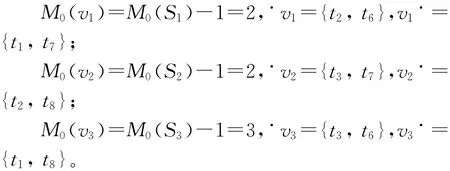
添加控制库所{v1,v2,v3}后的受控网是无死锁的,图1网的最大许可行为是42,而本算法添加控制器后的受控网有42个可达状态,说明该控制器是最大许可Petri网控制器。
再考虑一个结构稍微复杂一些的Petri网模型。图2所示为一个具有两个进程P1和P2的FMS的Petri网模型,这是一个S3PR网,它包含死锁,可达状态数为828。其中包括死标志38个、坏标志117个、危险标志96个、活标志577个,该网系统的最大可达状态(即可保留状态)为673个。网系统有3个严格极小信标S1={p2,p7,p13,p14,p15,p16,p17,p18},S2={p2,p7,p11,p13,p15,p16,p17,p18},S3={p2,p5,p13,p14,p17},它们的补集分别是[S1]=p3+p5+p6+p9+p10+p11+p12,[S2]=p5+p6+p9+p10,[S3]=p3+p11+p12。基于算法1可以得到一组GMEC为:
(l1,b1):M(p3)+M(p5)+M(p6)+M(p9)+M(p10)+M(p11)+M(p12)≤5-1=4,
(l2,b2):M(p5)+M(p6)+M(p9)+M(p10)≤4-1=3,
(l3,b3):M(p3)+M(p11)+M(p12)≤2-1=1。
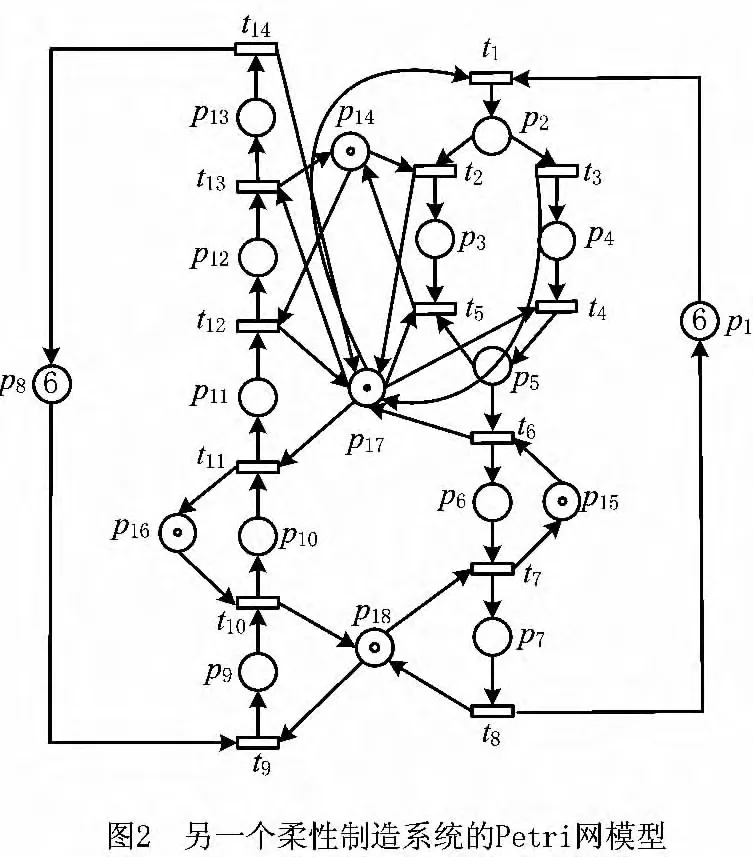
首先根据这些约束添加控制库所{v1,v2,v3},经分析可知添加了控制库所{v1,v2,v3}后的受控网N′中有死锁存在,即有新的可清空信标S4={p7,p12,p14,p16,p18,v2,v3},S5={p7,p11,p12,p16,p18,v2,v3},S6={p5,p6,p12,p14,v2,v3},S7={p5,p6,p11,p12,v2,v3}产生。基于算法1,很容易得到其补集分别为:[S4]=2p3+p5+p6+2p9+2p10+p11,M0′(S4)=6,[S5]=p3+p5+p6+2p9+2p10,M0′(S5)=5,[S6]=2p3+p9+p10+p11,M0′(S6)=4,[S7]=p3+p9+p10,M0′(S7)=3。
从而得到的另一组广义相互抑制约束为:
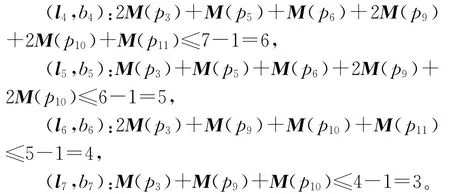
采用控制算法1对网系统再添加4个控制库所{v4,v5,v6,v7},则添加控制库所{v1,v2,v3,v4,v5,v6,v7}后的网记为(N′,M0′),且控制库所的初始资源数和前、后置分别为:
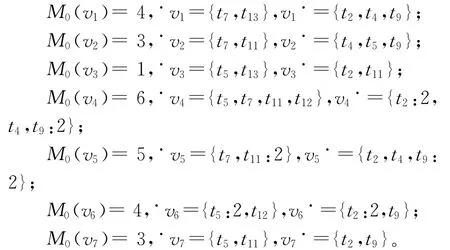
此时得到的受控网系统(N′,M0′)是无死锁的,且(N′,M0′)的可达状态为673个,即该控制器具有最大许可行为。
4 结束语
本文针对Petri网的一个子类——S3PR网,提出一种有效的死锁预防最优化策略,利用信标理论,采用迭代方法对网系统中所有可能出现的可清空严格极小信标添加基于广义互斥约束的控制器,使得系统的所有禁止状态不可达,即将网系统的所有可达状态限制为可保留状态,从而保证系统不存在死锁的状态和步骤。对可达状态性能要求比较高的、结构相对简单的网模型按本文策略进行控制,可以得到活的、最大许可行为的Petri网控制器。下一步将主要针对降低死锁预防最优化控制策略的算法复杂度以及所获得的最优控制器的结构复杂性进行研究。
[1] EZPELETA J,COLOM 段 ,MARTINEZ J.A Petri net based deadlock prevention policy for flexible manufacturing system[J].IEEE Transactions on Robotics Automation,1995,11(2):173-184.
[2] UZAM M,ZHOU 段 .An iterative synthesis approach to Petri net based deadlock prevention policy for flexible manufacturing systems[J].IEEE Transactions on Systems,Man,and Cybernetics:Part A,2007,37(3):362-371.
[3] GIUA A,SEATZU C.Liveness enforcing supervisors for railway networks using ES2PR Petri nets[C]//Proceedings of the 6th International Workshop on Discrete Event Systems.Washington,D.C.,USA:IEEE,2002:55-66.
[4] GIUA A,DICESARE F,SILVA M.Generalized mutual exclusion constraints on nets with uncontrollable translations[C]//Proceedings of the 1992IEEE International Conference on Systems,Man and Cybernetics.Washington,D.C.,USA:IEEE,1992:974-979.
[5] PIRODDI L,COSSALTER M,FERRARINI I.A resource decoupling approach for deadlock prevention in FMS[J].International Journal of Advanced Manufacturing Technology,2009,40(1/2):157-170.
[6] LI Zhiwu,HU Heshan,WANG Anrong.Design of livenessenforcing supervisors for flexible manufacturing systems using Petri nets[J].IEEE Transactions on Systems,Man,and Cybernetics:Part C,2007,37(4):517-526.
[7] HUANG 段 .Deadlock prevention for sequence resource allocation systems[J].Journal of Information Science and Engineering,2007,23(1):215-231.
[8] YAN Mingming,LI Zhiwu,WEI Na,et al.Optimal deadlock prevention policy for a class of Petri nets S3PMR[J].Computer Integrated Manufacturing Systems,2008,14(1):107-112,117(in Chinese).[闫明明,李志武,韦 娜,等.S3PMR网的一种死锁预防优化策略[J].计算机集成制造系统,2008,14(1):107-112,117.]
[9] YAN Mingming,ZHAO Mi.Maximally permissive deadlock prevention policy for FMS based on siphons[C]//Proceedings of the International Conference on Mechanic Automation and Control Engineering.Washington,D.C.,USA:IEEE,2010:3319-3322.
[10] LI Zhiwu,ZHOU Mengchu,JENG 段 .A maximally permissive deadlock prevention policy for FMS based on Petri net siphon control and the theory of regions[J].IEEE Transactions on Automation Science and Engineering,2008,5(1):182-188.
[11] MURATA T.Petri nets:properties analysis and applications[J].Proceedings of the IEEE,1989,77(4):541-579.

