矿尘防治措施效果评价统计分析方法及其应用

宫良伟 田卫东

(重庆工程职业技术学院矿业与环境工程学院)

矿尘监测是考察矿山企业执行国家粉尘卫生标准的重要手段［1］。利用矿尘的监测样本(定点采样或个体采样)数据可以比较工作场所(如采掘工作面等)在采取某种防治措施后的减尘效果，或者比较整个矿井前后2个时期矿尘治理的总体水平，作为矿井矿尘治理或措施效果的评价依据。如果这种比较仅仅对比前后2组矿尘监测样本的平均值，并根据平均值的大小进行判断，其说服力就不强;因为均值是随机变量，前后2个均值的不同可能是随机误差造成的，并不代表措施前后2个样本总体(或前后2个时期的矿尘治理水平)有差别。要合理的比较矿尘治理效果，必须利用科学的统计分析方法。

1 矿尘样本中离群值的判断和处理

1.1 离群值及其产生原因

在对矿尘样本进行统计分析前，需要对样本数据进行整理。在矿尘样本中，有1个(或几个)值与其他值相差很远，意味着它(或它们)可能来自于不同的总体。这个(或这些)值被称为离群值。根据显著性水平的不同，离群值分为统计离群值和歧离值。在剔除水平下显著的离群值是统计离群值，而在检出水平下显著但剔除水平下不显著的离群值叫歧离值。为检出离群值而指定的统计检验的显著性水平，即为检出水平，用α表示。为检出离群值是否高度离群而指定的统计检验的显著性水平，即为剔除水平，用 α*表示［2］。规定，检出水平 α 取0.05，剔除水平 α*取0.01。

离群值的产生有2个原因，一是随机因素造成的，即总体固有变异性的极端表现，离群值和其他值来源于同一总体;二是监测失误造成的，即观测、记录、计算错误引起的，离群值和样本中的其他值不属于同一总体。若能确定是后者引起的离群值，则予

以剔除或修改。若不能确定离群值产生的原因，本研究建议保留歧离值，剔除统计离群值。

1.2 离群值的检验方法和步骤

离群值的检验方法很多［3-4］。这里使用格拉布斯检验法来说明离群值的检验。检验前对样本进行从小到大排序。设原样本为x1，x2，…，xn，从小到大排序后为 x(1)，x(2)，…，x(n)，即 x(1)≤ x(2)≤ … ≤x(n)。离群值检验有单侧情形(包括上侧情形和下侧情形)和双侧情形。这里用双侧情形来说明，步骤如下:

(1)计算出统计量Gn和G'n的值。样本均值:

样本标准差

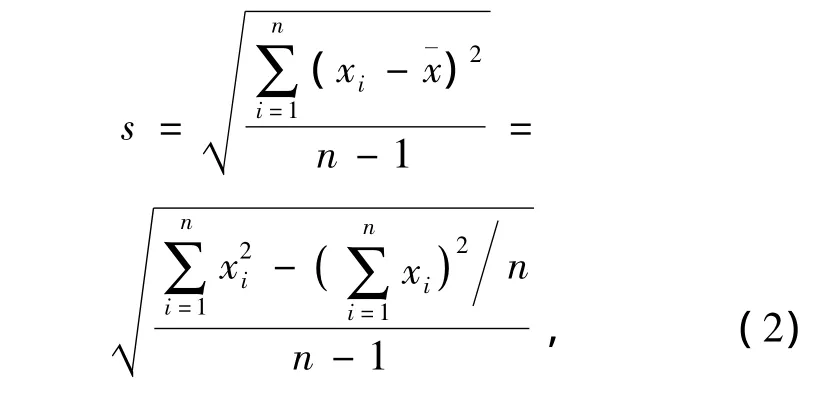
上侧情形统计量

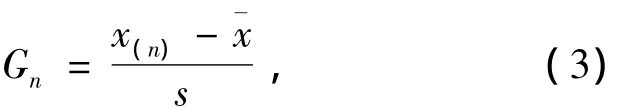
(2)确定检出水平α，在文献［2］表A2中查出临界值 G1－α/2(n)。

(3)当Gn＞ G'n且Gn＞ G1－α/2(n)时，判定x(n)是离群值;当G'n＞ Gn且G'n＞ G1－α/2(n)时，判定x(1)是离群值;否则判未发现离群值。

(4)对于检出的离群值x(1)或x(n)，确定剔除水平 α*，在文献［2］表 A2 中查出临界值 G1－α*/2(n)。当G'n＞G1－α*/2(n)时，判定x(1)为统计离群值，否则判未发现x(1)是统计离群值(即x(1)为歧离值);当Gn＞ G1－α*/2(n)，判断x(n)是统计离群值，否则判未发现x(n)是统计离群值(即x(n)是歧离值)。

1.3 矿尘样本离群值检验实例

某矿采煤工作面呼吸性粉尘测定样本数据为0.79、0.19、0.44、0.68、4.36、0.36、0.42 和 0.53 mg/m3。根据以往经验，离群值既可能是高端值也可能是低端值，利用格拉布斯检验法判断该样本是

下侧情形统计量否含有离群值。在计算前排序，x(1)=0.19，x(8)=4.36。根据式(1)计算珋x=0，97，根据式(2)计算s=1.38。

(1)计算出统计量G8和G'8的值。

(2)确定检出水平α=0.05，在文献［2］表 A2中查出临界值G0.995(8)=2.274。

(3)由于G8＞G'8且G8＞G0.975(8)，可以判4.36是离群值，0.19不是离群值。

(4)给出剔除水平α*=0.01，在文献［2］表A2中查出临界值G0.995(8)=2.274。由于G8＞G0.995(8)，判断4.36是统计离群值，应给予剔除。

2 局部区域矿尘样本比较统计分析方法

矿井局部区域在采取防尘措施前后分别测定一个矿尘浓度样本。局部区域矿尘样本总体分布近似符合正态分布。可使用2个独立样本均值假设检验的方法进行效果对比。样本均值比较方法视样本方差是否齐性而定［5］。样本齐性时采用t检验;非齐性时采用近似t检验，即t'检验［6］。因此首先需要进行前后样本方差齐性检验，然后根据检验结果选择适当的方法进行样本均值比较。

2.1 粉尘样本方差齐性检验

样本方差齐性检验的目的是决定样本均值的比较方法。根据粉尘样本方差检验的实际意义，应该是双侧检验［7］，即原假设 H0是=，备择假设H1是≠。显著性水平定为α =0.05。检验统计量计算公式为

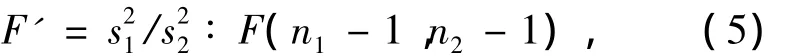
式中，s1和s2分别是前后2个粉尘样本的标准差，其计算式参考式(2)。该检验统计量符合F分布。然后通过查文献［4］的附表 A5，查出 F1－α/2(n1－ 1，n2－1)、F1－α/2(n2－ 1，n1－ 1)的值，并计算:1/F1－α/2(n2－1，n1－1)。根据查表结果和计算的值进行判断，即当

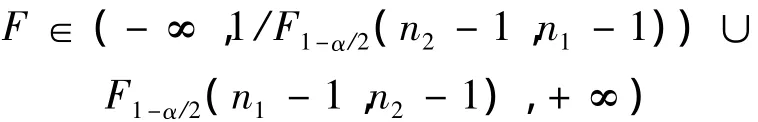
时，拒绝方差齐性的假设(2个矿尘样本方差差异显著);否则接受方差齐性的假设(样本间方差差别不显著)。

2.2 矿尘样本间均值比较

为便于矿尘样本间均值的考察和比较，显著性水平定为α=0.05和α*=0.01。并规定在α=0.05下显著的，称为“差异显著”;在α*=0.01下显著的，称为“差异异常显著”。依常理，矿井工作场所采取降尘措施后，粉尘浓度应该低于措施采取前的浓度。因此应采取单侧检验，即原假设H0∶μ1=μ2，备择假设 H1∶μ1＞ μ2。

当矿尘样本间方差检验为齐性时(样本间方差差别不显著)，使用t检验比较前后2样本间的均值。检验统计量按下式计算［7］:

式中，x1和x2为前后2矿尘样本的均值，按式(1)计算;s1和s2是标准差，计算方法参照式(2)。查阅文献［2］的附表A2，查出t0.95(n1+n2－2)和t0.99(n1+n2－2)的值。根据计算和查表结果进行判断:当t0.99(n1+n2－2)＞ tn1+n2－2＞ t0.95(n1+n2－2)时，前后2个矿尘样本均值“差别显著”，即采取措施后矿尘浓度降低明显;当tn1+n2－2＞t0.99(n1+n2－2)时，前后2个矿尘样本均值“差别异常显著”，即采取措施后矿尘浓度降低异常明显。否则，承认原假设，即采取措施后矿尘浓度没有明显降低。

当矿尘样本方差检验为非齐性时(样本间方差差别显著)，采用近似t检验，即t'检验比较前后2样本间的均值。检验统计量按下式计算:

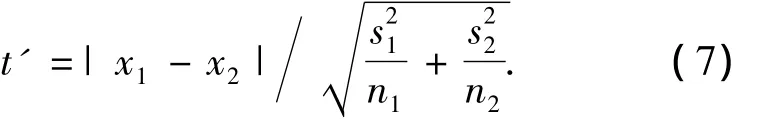
查阅文献［2］的附表 A2，查出 t0.95(n1－1)和t0.95(n2－1)及t0.99(n1－1)和t0.99(n2－1)的值，并计算:

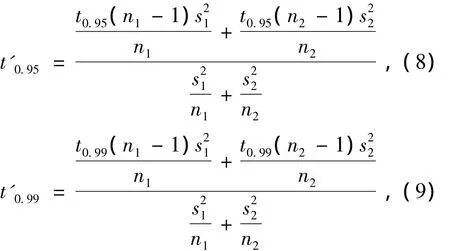
根据计算和查表结果进行判断:当t'0.99＞t'＞t'0.95时，前后2个矿尘样本均值“差别显著”，即采取措施后矿尘浓度降低明显;当t'＞t'0.99时，前后2个矿尘样本均值“差别异常显著”，即采取措施后矿尘浓度降低异常明显。否则，承认原假设，即采取措施后矿尘浓度没有明显降低。

3 矿井整体环境样本统计比较方法

在矿井空气环境评价中，需要对矿井内各种工作场所的粉尘进行监测，以期得到矿井环境的综合评价。一个时期在矿井内不同工作场所测定的粉尘数据样本显然不符合正态分布。对比矿井2个不同时期的粉尘浓度，直接使用上面的方法是不行的。需要对2个时期的测定的粉尘样本数据转换为常用对数，转换后的数据近似符合正态分布［8－9］。然后利用上面介绍的方法进行对比。由于原始数据的常用对数组成的两组新的样本近似符合正态分布，就可以使用上述方法进行统计分析了。

4 应用

润湿捕尘剂是一种添加剂，是具有分散和打湿功能、提高喷雾降尘效率的抑尘剂。为了了解其降尘效果，某润湿捕尘剂厂商在淮北桃园矿进行了降尘试验。试验在该矿Ⅱ1024里机巷综掘工作面进行。在掘进机后30～40 m处安装3道全断面喷雾［10］。分别测定普通水源和添加捕尘剂的全尘浓度，测定地点在3道全断面喷雾后50 m处。测定分别在掘进机作业和非掘进机作业(多工序)时进行。测定后对离群值进行了处理，处理后的数据见表1。

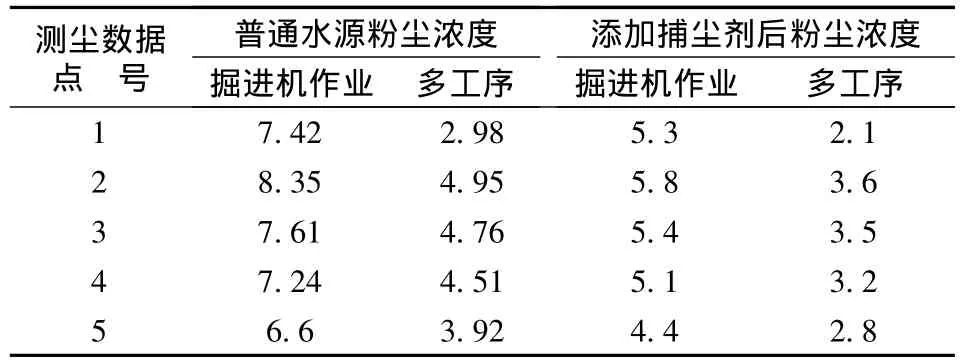
表1 掘进工作面粉尘浓度数据对照 mg/m3

粉尘测定是在同一地点进行的，测定数据符合正态分布。设定普通水源全断面喷雾在掘进机作业时粉尘浓度 X掘1～ N(μ掘1)，多工序时 Y多1～N(，);添加捕尘剂后粉尘浓度 X～掘2N(μ掘2，)，多工序时 Y多2～ N(μ多2，)。μ掘1，，，;μ ，μ，都未知。多1多2

(1)掘进机作业粉尘均值比较。第一步:矿尘样本方差齐性检验。双侧检验，原假设H0∶=，备择假设H1∶≠。根据式(5)计算检验统计量在显著性水平α=0.05下，查表并计算F0.975(4，4)=9.6、1/F0.975(4，4)=0.104 2。由于1/F0.975(4，4)＜F＜F0.975(4，4)，承认原假设，即矿尘方差样本方差为齐性。第二步:由于方差齐性，利用t检验进行矿尘样本均值比较。单侧检验，原假设H0∶μ掘1=μ掘2，备择假设 H1∶μ掘1＜ μ掘2。根据式(6)计算检验统计量 t8=5.5。查表 t0.95(8)=1.859 5(α =0.05)、t0.99(8)=2.896 5(α*=0.01)。由于 t8=5.5＞t0.99(8)=2.896 5，得出如下结论:添加捕尘剂前后2个掘进机作业工序矿尘样本均值“差别异常显著”，即采取添加捕尘剂后掘进机作业矿尘浓度降低异常明显。

(2)多工序粉尘均值比较。第一步:矿尘样本方差齐性检验。双侧检验，原假设H0∶=，备择假设H1∶≠。根据式(5)计算检验统计量

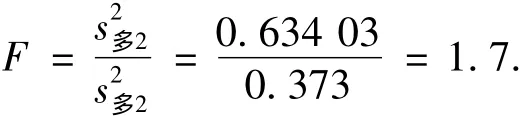
在显著性水平α=0.05下，查表并计算F0.975(4，4)=9.6、1/F0.975(4，4)=0.104 2。由于1/F0.975(4，4)＜F＜F0.975(4，4)，承认原假设，即矿尘方差样本方差为齐性。第二步:由于方差齐性，利用t检验进行矿尘样本均值比较。单侧检验，原假设H0:μ多1=μ多2，备择假设 H1:μ多1＜ μ多2。根据式(6)计算检验统计量 t8=2.36。查表 t0.95(8)=1.859 5(α =0.05)、t0.99(8)=2.896 5(α*=0.01)。由于 t8=2.36＞t0.95(8)=1.859 5，得出如下结论:添加捕尘剂前后多工序作业矿尘样本均值“差别显著”，即采取添加捕尘剂后多工序作业矿尘浓度降低明显。

通过不同的工序对比，可以得出结论:淮北桃园矿Ⅱ1024里机巷综掘工作面在添加捕尘剂后的喷雾降尘效果得到了明显改善。

［1］ 浑宝炬，郭立稳．矿井粉尘检测与防治技术［M］.北京:化学工业出版社，2005．

［2］ 中国标准化研究院．GB/T 4883—2008 数据的统计处理和解释:正态样本离群值的判断和处理［S］.北京:中国标准出版社，2009．

［3］ 赵辉，邵素华，谢东坡.分析数据中离群值的处理方法［J］.周口师范学院学报，2004，21(5):70-73.

［4］ 邓 勃.关于异常值的检验与处理［J］.大学化学，1995，10(4):5-9.

［5］ 胡良平，高 辉.如何正确运用t检验［J］.中西医结合学报，2008，6(2):209-212.

［6］ 王文周.改良 t检验法［J］.西华大学学报，2008，27(6):91-94.

［7］ 中国标准化研究院.GB/T 4889—2008 数据的统计处理与解释:正态分布均值和方差的估计与检验［S］.北京:中国标准出版社，2009.

［8］ 国家安全监督管理总局．AQ 4205—2008 矿山个体呼吸性粉尘测定方法［S］.北京:煤炭工业出版社，2009．

［9］ 金龙哲，李晋平，孙玉福.矿井粉尘防治理论［M］.北京:科学出版社，2009.

［10］ 张友根.桃园矿推广综掘工作面综合防尘系列化［J］.矿业科学技术，2011，39(3):153-154.