内外兼修 创设有效数学问题情境

■陆丽

内外兼修 创设有效数学问题情境

■陆丽

10.3969/j.issn.1671-489X.2013.14.049

从问题情境的外壳和内核两方面入手，借助实例，说明创设问题的有效情境首先可以从改变反映思维对象和内容的数学问题出发，将抽象的内容直观化，零散的知识系统化，固定的思维开放化；也可以适当调整问题情境载体的呈现方式，让问题情境生活化、活动化和情趣化。

数学课程标准（2011年版）指出：“数学教学应该从学生实际出发，创设有助于学生自主学习的问题情境。”所谓问题情境，其实就是将数学问题融于现实的背景资料中，教师通过设立一系列有适当难度的问题活跃学生的思维，激发学生的学习需要，改变学生在教学中的地位——从被动的知识接受者转变成为知识的共同建构者，从而唤起学生的问题意识、参与意识和合作意识，使学生在问题情境中产生好奇、渴求、探究、协作、交流等学习欲望和活动，从而让学生有机会经历“问题情境——建立模型——解释或应用”这一重要的数学活动过程，从而获得对数学的真正理解。

1 内“修”：促进数学知识的理解

1.1 呈现：直观化

数学来源于生活，学生对于一些数学概念并非一无所知，往往有着自己的一些独特的感知和理解，但是这些生活经验往往是粗浅的、不系统的，甚至是错误的。教师可以利用直观的教学素材，紧扣住学生认知经验和数学概念之间的矛盾，利用鲜活、可用的生活经验，创设出有效的问题情境。

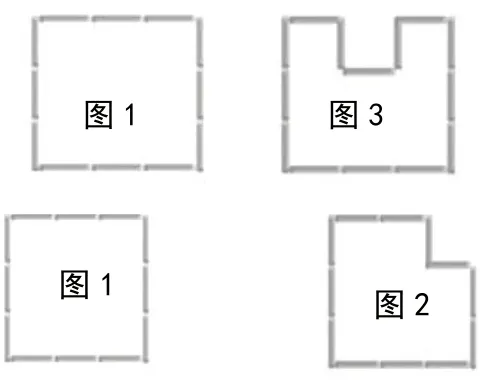
如在学习了周长的知识之后，学生借助于日常的生活经验，往往会认为大的（指面积）图形的周长一定大。根据学生的学情，教者运用两组几何图形的直观比较顺利地解决了这个问题。首先出示图1和图2，学生经过观察发现，两个图形的样子明明不一样，但是周长却相等，从而得出第一个结论：周长相等的图形形状可能不相同。接着呈现出图1和图3，这一操作活动让学生发现，小的（指面积）图形的周长还比大的（面积）图形大。这种有悖于“常理”的事实触发了学生的认知矛盾。在解决这个问题的过程中，学生把注意力集中到围成图形的小棒的根数，关注小棒根数的多少，其实也就是关注了周长这个概念的本质属性，即一周边线的长短，从而顺利地解决了问题。

1.2 链接：系统化

如教学“长方形面积的计算”的时候，学生已经认识到要知道一个图形的面积是多少，只要看其中包含了多少个面积单位。那么想要知道一些规则图形如长方形的面积是多少，又可以怎样来测量呢？长方形的面积计算公式是长乘宽，那么这个公式是怎么得来的呢？为什么可以用长乘宽的积来表示长方形的面积呢？教师通过创设问题情境，引导学生回忆旧知识，让学生从能直接数出面积单位的个数到利用乘法算出面积单位的个数，从而逐步导出长方形的面积计算公式。由此可见，根据数学知识内在的逻辑关系创设问题情境，也不失为学生开展数学学习的好素材。

1.3 思维：开放化

有效的问题情境必然饱含鲜明丰富的数学内涵，教师要引导学生透过现实情境，对问题情境的非数学本质属性进行剥离和剔除，从而凸显数学本质，实现数学化的过程。

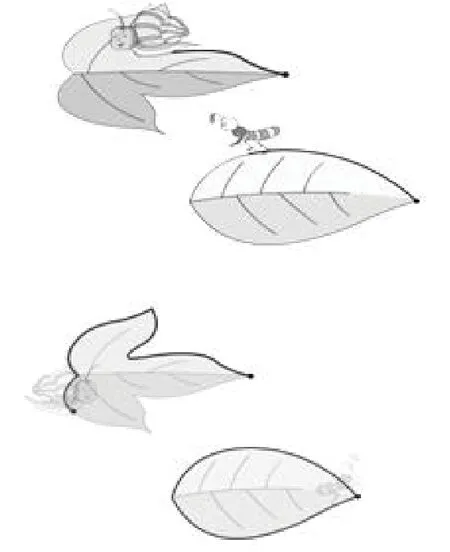
图4

2 外“修”：让数学变得好“玩”

2.1 方式：活动化

课标指出，要让学生积累基本的数学活动经验。数学活动经验从何而来呢？在教学中，教师应精心创设活动化的问题情境，让学生在做中学、玩中学，探索新知，积累数学活动经验。

在求周长的实践活动中，让学生充分体会到测量一些物体表面周长的方法可以用绳子围，用直尺直接测量等。但是实际测量时又应该怎样合理地选择方法呢？这样选择的理由又是什么呢？带着这样的问题，学生依次测量不规则图形（如树叶面）、规则图形（如五边形，三角形等）、特殊图形（正方形，长方形等）的周长，学生在自主体验活动中感悟出：应该根据实际情况合理选择方法，同时使学生加深对周长的认识，初步感知化曲为直的数学思想方法。

2.2 包装：生活化

教学“认识一元以内的人民币”，由于学生已经认识了面值是一元及以下的人民币，并且在日常生活的买卖过程中体会到了元和角之间有关系，但是具体是什么关系却不是很清楚，于是教师就在课堂上模拟了一个购物情境，以解决这个问题。画面定格在小明的问题：“要付1元，可我只有角票，我该怎么取钱呢？”“同学们，请你们帮帮小明取出1元钱。”学生仿佛就化身为小明，在教师精心创设的问题情境中，积极性异常高涨。他们结合自己已有的生活经验，设身处地地为小明想出多种多样的方法：“可以取出2张5角”“可以取出10张1角”“还可以这样拿，2张角，1张1角，1张5角”……而这些方法只是他们的生活经验而已。

“两张5角合起来不是10角吗？怎么会是1元呀？”这个问题的提出及时地引导学生意识到元与角之间有关系，并且1元就等于10角。如果教师在创设问题情境的时候，能够准确把握学生学习的现实起点，尽可能地了解学生的生活环境和生活经验，让存在于学生现实生活中的相关信息有机融入课堂学习活动中，教学时就能达到事半功倍的效果。

2.3 手段：情趣化

小学生天性爱动喜变化，如果常用单调机械的形式进行教学，学生就会产生厌烦情绪。因此，教学的时候就必须借助于多样化、新颖化的教学手段，帮助他们从厌倦的情绪中解放出来，让他们主动参与到学习中来。同时创设的情境还能凸显所授知识的本质特征，弱化非本质特征对概念的干扰和负影响。

如建立周长的概念、理解周长的含义是教学的重点，也是教学的难点。如何突出重点、突破难点呢？笔者以蚂蚁和蜗牛在“运动场”（树叶）上跑步这一生动有趣的童话情境为载体，激起学生求知的欲望。如图4所示，首先通过电脑动画演示，让学生发现两种小动物都是沿着树叶的边线走的。接着通过进一步观察发现：蚂蚁沿着树叶的边线走了一周，蜗牛沿着树叶的边线没走完一周。到这时候，虽没有直接下周长的定义，但对其本质属性的感知训练非常的细致到位。借助多媒体操作演示，通过求同存异的比较，帮助学生清晰、深刻地感知周长概念的本质属性——“边线”和“一周”，接下来周长概念的揭示就显得水到渠成了。顺势而发，课件出示一只蜘蛛，虽然走完一周，但是没有沿着边线走这个画面，经过辨析比较，进一步强化了对周长的认识。由此可见，抽象的数学知识要能够调动起学生的学习兴趣和主观愿望，创设富有情趣化的数学问题情境就显得尤为重要。

3 结语

综上所述，有效的问题情境应该是内外兼修的，既要满足学生好玩有趣的需求，又要调动学生的探索欲望，促进学生数学学习能力的提升。正如郑毓信教授所言：“好的数学情境，应该满足一个基本的要求……不应该仅仅起到敲门砖的作用，也不仅仅有益于调动学生的积极性，而应该在课堂的进一步开展中自始至终发挥一定的导向作用。”

江苏省江阴市晨光实验小学）