例谈化归思想在数学解题中的应用

郭 靖

(陕西省山阳中学，陕西 山阳 726400)

我们知道整个中学数学内容，始终贯穿着数学知识和数学方法这两条线。化归方法是中学数学中的重要数学方法之一。所谓“化归”就是转化和归结的简称。化归方法是数学解决问题的一般方法。其基本思想是：人们在解决数学问题时，常常是将待解决的问题A通过某种转化手段，归结为另一个问题B，而问题B是相对较易解决或已有固定解决程式的问题，且通过对问题B的解决可得原问题A的解答。

下面就化归思想在中学数学解题中的应用结合例题谈几点笔者的体会。

1 由此及彼，将陌生的问题熟悉化

将陌生的问题向已知熟悉的知识转化，使之能用熟悉的知识和方法解决新的问题。这种转化常常可达到事半功倍的效果，使一些陌生的新问题变得迎刃而解。例如，在一次作业批改过程中，我发现学生对下面一道题目做错的特别多：

讲评时，我并没有直接就题讲题，而是给出了下面一道题目：

对于变式题，同学们很快给出了正确解答——“1”的代换，再用基本不等式，这是同学们早已熟悉了的一种常用方法。接着，我又引导同学们比较两题目的区别与联系：显然，在0＜x＜的条件下，sinx＞0，1-sinx＞0 且 sinx+（1-sinx）=1， 若令 a=sinx，b=1-sinx 则两问题本质上完全相同。至此，同学们恍然大悟，感叹道：“这真是：山穷水复凝无路，柳暗花明又一村”——此化归之妙哉！

2 学会逆向思维，将复杂问题单化

复杂问题简单化是数学解题中运用最普遍的思考方法，一个难以直接解决的问题通过对问题深入观察和研究，转化成简单的问题迅速求解。例如：

【说明】（1）﹑（2）两问较为容易，在此不再赘述。 （3）问标答所给的证明方法中学生接受起来有一定的困难，在一次高考复课研讨会上，讲课老师曾给出了多种证法，但所用到的知识均有超出中学所学知识范围之嫌，在现行的新课标中，教材虽有所涉及，但均属选修内容，且难度较大。事实上，我们围绕目标分析，经过一系列的化归不难解决。

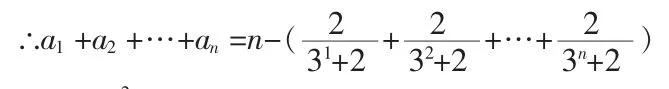
又

又由数学归纳法容易证明，当n≥3时，3n＞2（n2+n）即

故原不等式成立。

这样，使得一些表面看似很复杂的问题，通过一步一步的化归转化变得也不再十分复杂。

3 构造模型，使一些棘手问题简单化

在新课程标准中，明确提出“让学生学有用的数学”，把数学的实际应用能力提高到了一个非常重要的地位，函数、数列……中学课本所有内容无不体现这一重要思想，而要把一个实际问题用数学知识来解决，数学建模能力的培养也就自然成了重中之重，因此在日常的教学中，我们应该潜意识的注重培养学生一些基本的数学模型能力。例如：

例3 (07广东高考理科第12题)如果一个凸多面体为n棱锥，那么这个凸多面体的所有顶点所确定的直线共有_____条。这些直线中共有 f（n）对异面直线，则 f（4）=_____；f（n）＝_____。 （答案用数字或 n的解析式表示）

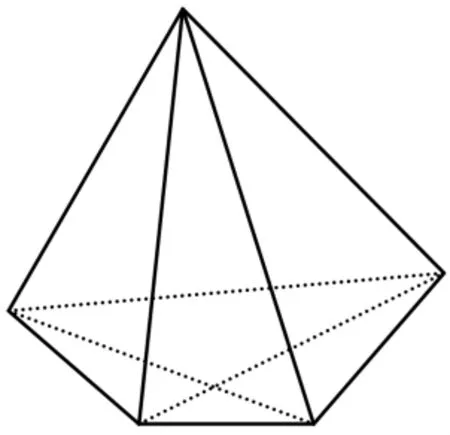
图1

分析：因为n棱锥共有n+1个顶点，任意两点可连一直线，故所有顶点所确定的直线共有

对于f（n）的计算可将问题化归为过这n+1个顶点可构成多少个三棱锥，因为一个三棱锥中共有3对异面直线——这是我们所熟悉的问题。而n棱锥的n+1个顶点中，任选四个能构成三棱锥的必含棱锥顶点，再从底面的n个顶点中人选3个，故，进而易得 f（4）=12。

总之，在数学中化归的思想与方法几乎是无处不在，无时不在。化归的思想在数学的研究和学习中应用十分广泛，重视这种方法在数学解题教学中的运用，对学生思维的灵活性、广阔性、敏捷性、创造性，及去发现问题、探索问题、解决问题的能力将有重要的意义。

从广义上说，数学问题的求解都是运用已知条件对问题进行一连串恰当转化归结，进而达到解题目的一个探索过程，熟练、恰当的转化可以迅速、准确地解决问题。灵活的转化可以出方法、出速度。而数学问题中运用化归思想解题的例子比比皆是，绝不是几种类型可以加以概括的，平时教学中，只要我们教师具有化归的思想意识，深入钻研教材、挖掘和提炼中学数学内容的转化矛盾思想，针对不同的问题，缜密思考，及时总结各种“转化归结”方法，有意识地加强化归方法的教学，对于培养造就“发现”、“创新”型人才具有十分深远的意义。

［1］张景斌，主编.中学数学教学教程[M].

［2］王子兴.数学方法论[M].

［3］苏炳堂.浅谈化归思想在中学数学中的应用[J].中小学教育，2010（11）.