在微积分教学中融入数学建模思想

庞 亮

（华中农业大学 楚天学院，湖北 武汉430205）

0 引言

近十余年，我国普遍兴起了数学建模教学和数学建模竞赛，推动了高校数学的教学改革。数学建模是沟通数学理论与实际问题的中介和桥梁，培养学生数学建模能力是提高数学思维和应用能力的重要手段，在微积分教学过程中穿插建模能力训练对学生是十分必要的。

2012年湖北省高等学校省级教学研究项目 “独立学院数学建模与大学生实践创新能力培养研究”和华中农业大学楚天学院教学研究项目《微积分优质课程建设》中，结合各专业特点，将本校微积分划分为四类，分别是微积分A，B，C，D，本文结合食生院学生的专业特点，尝试在微积分B教学中融入数学建模的思想。以实验室为基础、以学生为中心、以问题为主线，以培养能力为目标来组织教学工作。通过教学使学生了解利用数学理论和方法去分析和解决问题的全过程，提高他们分析问题和解决问题的能力；提高他们学习微积分的兴趣和应用微积分的意识和能力，使他们在以后的工作中能经常性地想到用数学去解决问题。教师利用一些事先设计好的问题启发学生主动查阅文献资料和学习新知识，鼓励学生积极开展讨论和辩论，培养学生从事科研工作的初步能力，培养学生团结协作精神，增强他们的数学素质和创新能力。

在实践中，数学建模的应用过程是复杂的，但也是有规律可循的。微积分B的特点是内容多，学时少，教师在完成教学任务的基础上，将数学建模的思想融入微积分B的教学中是存在困难的，这要求教师熟悉数学建模思想和方法，同时也要把握好微积分B的教学重点。

1 应用实例

我微积分B主要针对的三个专业分别是食品科学与工程，食品安全，生物工程。一些可以用微积分模型来描述的问题，如疾病传染、人口增长、种群竞争等问题，应在教学中引导学生通过建立数学模型来解决。一些重要模型的求解和分析应在教学中有所反映，比如Logisitic模型能描述人口、生态、广告等许多领域的问题。在微积分B教学中融入建模思想可以改善教学内容与应用脱节的状况，促进学生尽早接触微积分的应用领域，更好的激发学生学习的兴趣。下面我们举例说明微积分教学内容的“融入”数学建模思想的问题。

1.1 导数的应用

微分是函数的相对变化的极限过程。导数、微分在经济中的应用比较广泛，主要反映为边际、弹性等。在微积分B教学中通过数学建模将这部分知识与实际生活结合的实例主要表现有：食品的最佳销售时机，食品生产中机械与人工的调配问题等等。

1.2 函数极值的应用

极值问题是最优化模型求解的基础，在教学中可以插入利用最优化方法建模的思想，既使学生看到了导数在实践中的应用，也学会了建模的基本步骤。

例1 鱼贮量问题

一位鱼类生物学家对一个湖中的鱼贮量进行了研究，发现当每单位面积的水域有种鱼时，一个季度后，每种鱼的平均重量为：

W（n）=400-20n（单位；g），0≤n≤20.

试求当n为多少时，一个季度后，鱼的总重量达到最大？

分析：湖的面积是固定的，与鱼的种类n无关，因此当每单位面积水域的鱼重量最大时，湖里鱼的总重量最大。

解：每单位面积鱼的总重量为Y（n），根据题意：

Y（n）=W（n）×n=400n-20n2

Y'（n）=400-40n.

当 n=10 时，Y'（n）=0.

答：当n=10时，一个季度后，鱼的总重量达到最大。

1.3 微分方程与曲线积分的应用

微分方程和曲线积分的应用实例很多，比如人口模型，单种群动物模型，江河污染物的降解系数，放射性元素的衰变模型等等。这里主要介绍在微积分B教学过程中引入的模型实例。

例2 药物总量

设液体以5mL/s的速度将药物送人容积是300mL的容器中，且液体以相同的速度离开器官。如果进入液体中的药品的浓度是0.1g/mL，且时间t=0时，器官内没有药物。试求器官内药物总量关于时间的函数以及1min时器官内药物总量。

药物进入器官速率为 5（mL/s）×0.1（g/mL）＝0.5（g/s）.

又由于总量的变化率等于药物进入速率与离开速率之差，故：

这就是我们建立的微分方程模型。

将 x（0）=0 代入，得 c=-30.

1min 时器官内药物总量为 x（60）=30-30e-1≈18.96g.

例3 人口预报模型

问题：今年人口数量是n0,年增长率r0为常数，问t年后人口数会是多少。

模型构成：设时刻的人口数量为n（t0）

由分析得：n（t+△t）-n（t）=r·△t·n（t）

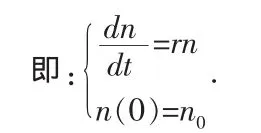
分离变量，两边积分即可得到。

例4 灰太狼抓羊的问题

一只羊在羊村北面80米处玩耍，灰太狼出现在羊的正东100米处。当两只动物同时发现对方以后，羊奔向羊村，灰太狼以快于羊一倍的速度紧追羊不放。灰太狼在追赶过程中所形成的轨迹就是追击曲线。灰太狼是否会在羊跑回羊村之前抓住羊？

分析：假设灰太狼奔跑的轨迹是连续曲线，以二者刚发现对方时羊所在位置为坐标原点，羊朝向灰太狼的方向为x轴正向。设任意时刻羊的坐标为（x1，y1），灰太狼的坐标为（x，y），显然灰太狼的奔跑轨迹可用方程 y=y（x）来描述。

提问：（让学生自己思考）

（1）计算任意时刻灰太狼的速度（利用导数求解切线方程进而解决速度问题）；

（2）假设二者都是匀速奔跑，则相同时间内二者奔跑路程的倍数关系就等于二者速度之间的倍数关系。尝试建立灰太狼从开始计算到任意时刻所奔跑的路程表达式（利用第一类曲线积分解决）。

2 结束语

微积分理论基础的建立是认识上的一个飞跃。极限概念揭示了“有限”与“无限”、“收敛”与“发散”、“间断”与“连续”等的辨证关系，是这对矛盾联系的桥梁。使学生了解“无限”建立在“有限”之上，渗透深刻的数学思想以及“变中有不变”、“有限”中有“无限”，“无限”中有“有限”的观点等。在介绍微积分知识体系的过程中，适当地融入数学模型思想，提高大学生的数学素质和人文精神。根据食生院学生特点，特别开设了数学建模选修课，使这些学生认识到，微积分的理论、方法在各自专业中的应用。另一方面，使学生对数学建模思维和应用数学知识解决实际问题的内容非常感兴趣，很多同学在大一就对数学建模有了一定的了解，大二的时候又积极参加全国数学建模竞赛，并获得了全国数学竞赛一等奖。这样同时也为他们学习后继课程打下了一定的基础，比如线性规划，概率统计，无机化学等等。

微积分教学中融入数学建模思想必然会受到越来越多的重视，这是解决办学效率和优秀人才培养之间矛盾的有效方法。适时的应用数学建模思想进行教学，可以促使教学方法得到改进，提高教学水平和教学效果，有助于推进高等数学的教学改革和课程建设的发展。

［1］谢季坚,李启文.大学数学[M].高等教育出版社,2009.

［2］戴朝寿，孙世良.数学建模简明教程[M].高等教育出版社,2007.

［3］庞亮.独立学院高等数学教学改革探讨[J].科技信息,2012,2012,17;185.