脉动风场的模拟方法及其在输电线路风振计算中的应用

沈国辉，黄俏俏，郭 勇，邢月龙，楼文娟，孙炳楠

（1．浙江大学 土木工程学系，浙江 杭州 310058；2．浙江省电力设计院，浙江 杭州 310007）

0 引 言

结构风振时程分析需要有作为输入的脉动风荷载，由于输电塔是格构式透空结构，不能像房屋结构那样采用测压试验获得脉动风荷载，因此需要采用人工模拟方法来获得。脉动风场的模拟主要是具有相关性的风速时程模拟，在风速时程基础上获得脉动风荷载时程。

脉动风场的模拟方法中，主要采用谐波合成法［1－4］（WAWS法）和线性滤波法［5－8］（AR 法）。以往的研究中，在输电塔的风场模拟方面以上两种方法均有采用［9－10］，在输电塔线体系的风场模拟上只有采用谐波分解法［11－12］的实例。在应用谐波合成法时，风谱有多种选择，算法也有很多，如基于快速傅里叶变换（FFT）［11］和基于特征值分解（POD）［13］等，模拟的风场还有一维风场［11］和三维风场的区分［12］。可见脉动风场的模拟有很多选择，使查阅这些文献的读者感到迷惑，同时根据笔者的广泛文献查阅，并没有研究针对各种方法的适用性和计算效率进行过对比，也没有研究比较过各种模拟方法得到的计算结果。

基于以上背景，本文应用各种脉动风场的模拟方法模拟出输电塔和塔线体系的脉动风场，考虑一维风场和三维风场情况，对比各种方法的计算效率和计算结果，分析各种模拟方法的适用性和等价性，最后讨论单塔和塔线体系风振计算结果的差异，对输电线路和其他构筑物的脉动风场模拟具有工程参考价值。

1 脉动风场的数值模拟方法综述

1．1 谐波合成法（WAWS法）

Rice［1］提出谐波合成法的基本思想，模拟一维单变量的平稳高斯随机过程。Shinozuka［2］提出用WAWS法模拟平稳随机场的基本理论，解决多变量均匀高斯随机过程，如下式所示：

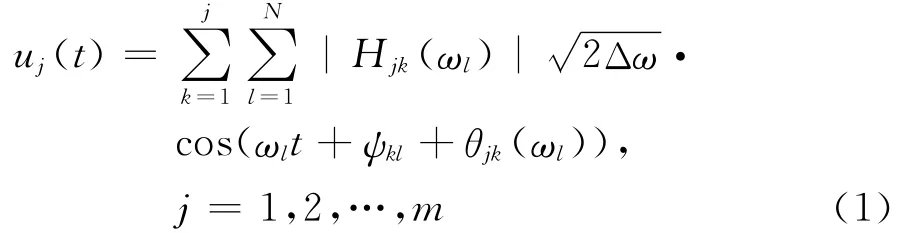
式中，Hik（ωl）为互功率谱密度矩阵S（ωl）的 Cholesky分解矩阵H（ωl）中的元素，ψkl为两个不同作用点之间的相位角，θik为介于0～2π之间均匀分布的随机数，m 为模拟的点数。Yang等［3］在计算中综合FFT技术，大大提高该类方法的计算效率。为获得较长的模拟周期，Deodatis［4］引入双索引频率概念，消除模拟过程中的周期性。

当模拟的点数较多时，需要对每一个模拟点的互谱密度矩阵进行Cholesky分解，计算量很大，同时考虑相位角后的互谱密度矩阵为复数矩阵，有可能变成不正定而导致互谱密度矩阵不能进行Cholesky分解。李黎等［13］用POD分解来代替Cholesky分解，解决了该问题，如下所示：

式中φk（ω）和ηk（ω）是S（ω）的特征向量和特征值。若前Ns阶振型包含的能量足够大，采用模态截断技术，可以大大提高计算效率：

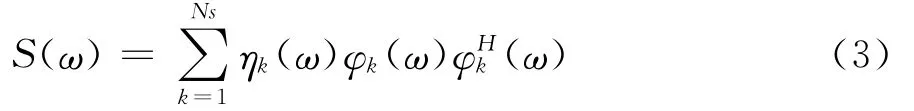
基于POD分解的WAWS法得到的随机风速时程模拟公式为：

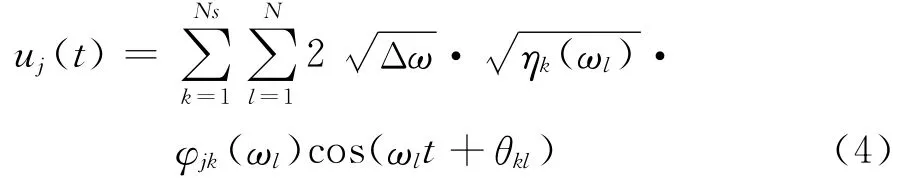
1．2 线性滤波器法（AR法）

Gerch等［5］首先提出将线性滤波技术用于生成随机时间序列等工程问题，Li等［6］对线性滤波法进行了不断改进，发展了可以用AR、ARMA等模型模拟多维多变量的随机过程，曾宪武［7］、鲍侃袁［8］等都在脉动风场模拟中应用了AR法。线性滤波器法实质上是由前面连续几个时刻的随机量来推导后面特定时刻的随机量，具有时间相关性。

AR法可考虑各个模拟点的空间相干性，但AR法不像WAWS法无条件收敛，时间步长不能太小，太小精度反而会降低，时间步长一般不小于0．1s。脉动风速时程可由下式来模拟：

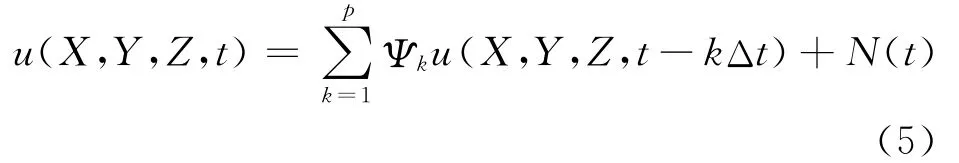
式中，X，Y，Z为坐标向量矩阵，p为模型阶数，Δt是模拟风速时程的时间步长，Ψk为自回归系数矩阵，N（t）为均值为零且具有给定协方差的正态分布随机过程。

2 输电线路的实例及其风场模拟

2．1 输电塔和塔线体系介绍

以某输电线路为例进行分析，输电塔总高为34m，呼称高为26m，塔身平面形状为正方形，如图1所示。输电线由3根导线和2根地线组成，导线的挂线绝缘子长度为3m，档距为300m。导（地）线型号及相关参数如表1所示。

表1 导（地）线的型号及参数Table 1 Model and characteristics of wire

单塔的有限元建模时采用三维梁单元来模拟输电塔的杆件，节点板和爬梯等采用质量单元来模拟，每个塔由564个梁单元和88个质量单元组成，单塔的有限元模型如图1所示。塔线体系包含两个输电塔和三档输电线，每档内输电线采用100个仅受拉的三维杆单元［14］来模拟，绝缘子采用三维杆单元来模拟，塔线体系的有限元模型如图2所示。

图1 单塔的有限元模型Fig．1 Finite element model of isolated tower

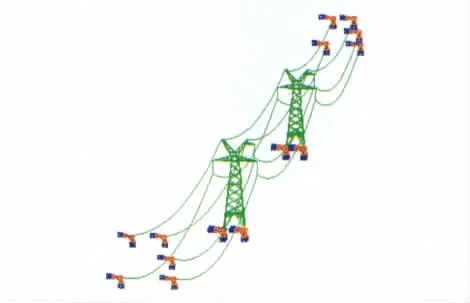
图2 塔线体系的有限元模型Fig．2 Finite element model of tower line system

2．2 输电塔和塔线体系的脉动风场模拟

针对输电塔和塔线体系分别模拟其顺风向的脉动风，本文以横导线方向作为正迎风方向。采用常见的3种方法进行风场模拟：（1）基于FFT变换的WAWS法（WAWS，FFT）；（2）基于POD分解算法的 WAWS法（WAWS，POD）；（3）AR 法。在基于POD分解算法的WAWS法计算中，单塔的截止振型数Ns取20，塔线体系的Ns取50，在AR法中自回归阶数p取4。

国内外很多学者给出了各种顺风向的风速谱，如Davenport谱、Harris谱和Kaimal谱等，本文计算采用Davenport谱：

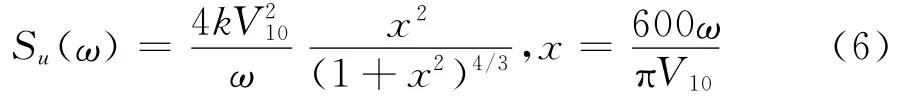
式中V10为10m高度的基本风速，k为地面粗糙度系数。

频域内脉动风的相干特性采用相干函数来表示，相干函数是沿距离远近呈指数衰减的曲线。常用的有Davenport相干函数、日本规范AIJ建议的相干函数和盐谷（Shiotani）相干函数。本文采用Davenport提出的相干函数［15］：

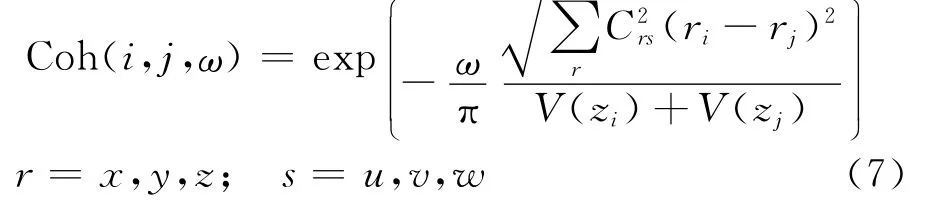
指数衰减系数为：

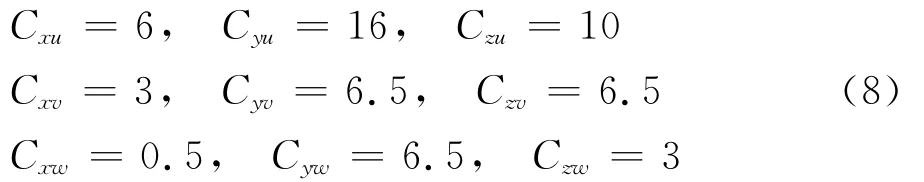
表2给出了脉动风场模拟的参数，其中单塔工况沿高度模拟34个点，分别对应于迎风面的各层节点；塔线体系包括两个输电塔和三档输电线，输电线中的导线和地线每隔30m设置一个模拟点，塔线体系共有227个模拟点。

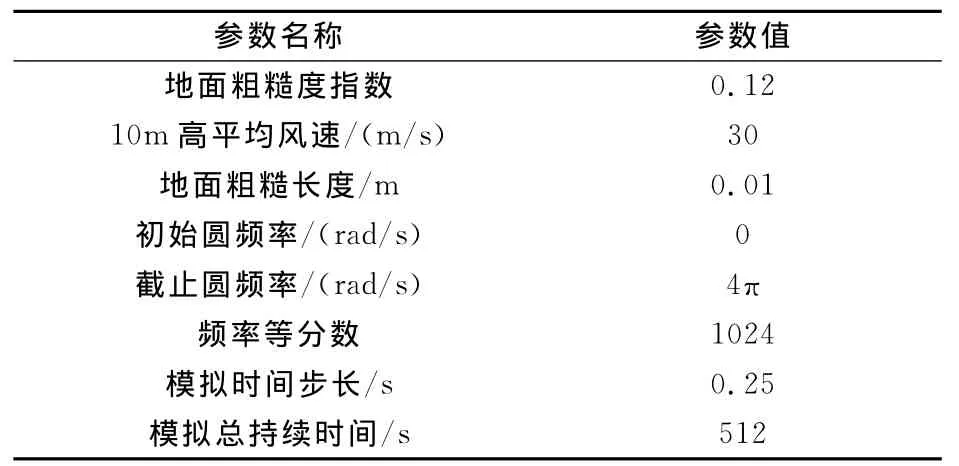
表2 各种模拟情况选取的参数Table 2 Calculating parameters used in different simulations

2．3 风振时程分析的计算方法

利用风场模拟方法得到风速时程，可转化得到脉动风荷载时程，作用于结构上任一点M坐标的瞬时风速u（M，t）由两部分组成：平均风速¯u（M）和脉动风速u′（M，t），根据准定常假定，结构上任意一点所受的风荷载F（M，t）计算公式为：式中ρ为空气的密度，CD为构件的截面阻力系数，A为该区域结构的迎风面积。将风荷载直接施加于输电塔和塔线体系的三维有限元模型上相应层的各个节点上，采用Newmark法进行时程分析，计算中考虑结构的几何非线性。

3 基于一维风场模拟的计算结果

一维风场只考虑顺风向，只用顺风向的风速谱进行分析，不考虑横风向、竖直向与顺风向的相关性。

3．1 单塔情况下的风致响应

分别采用上述三种脉动风场的模拟方法，模拟单塔34个节点的风速时程，三种模拟方法的计算效率如表3所示。表3中的所有数据为在同一台计算机中的计算时间，表3中括号内数字表示模拟的点数，一维表示模拟一维风场，三维表示模拟三维风场。由表3的第一行数据可知，三种方法都可以进行单塔在一维风场下的数值模拟，速度均较快。

表3 各种工况下各种方法的计算效率Table 3 Calculating efficiency of different simulations using different methods

为了验证上述三种方法模拟脉动风速时程的有效性，用PSD函数对风速时程求自功率谱S（n），与Davenport谱进行比较，第30个模拟点的PSD谱和Davenport谱的比较见图3。由图3可知，上述三种方法模拟获得的风速时程PSD谱和目标谱吻合很好，说明上述三种方法均能有效地模拟随机风速时程。三种方法的相干性也吻合较好，限于篇幅，在此不再给出。

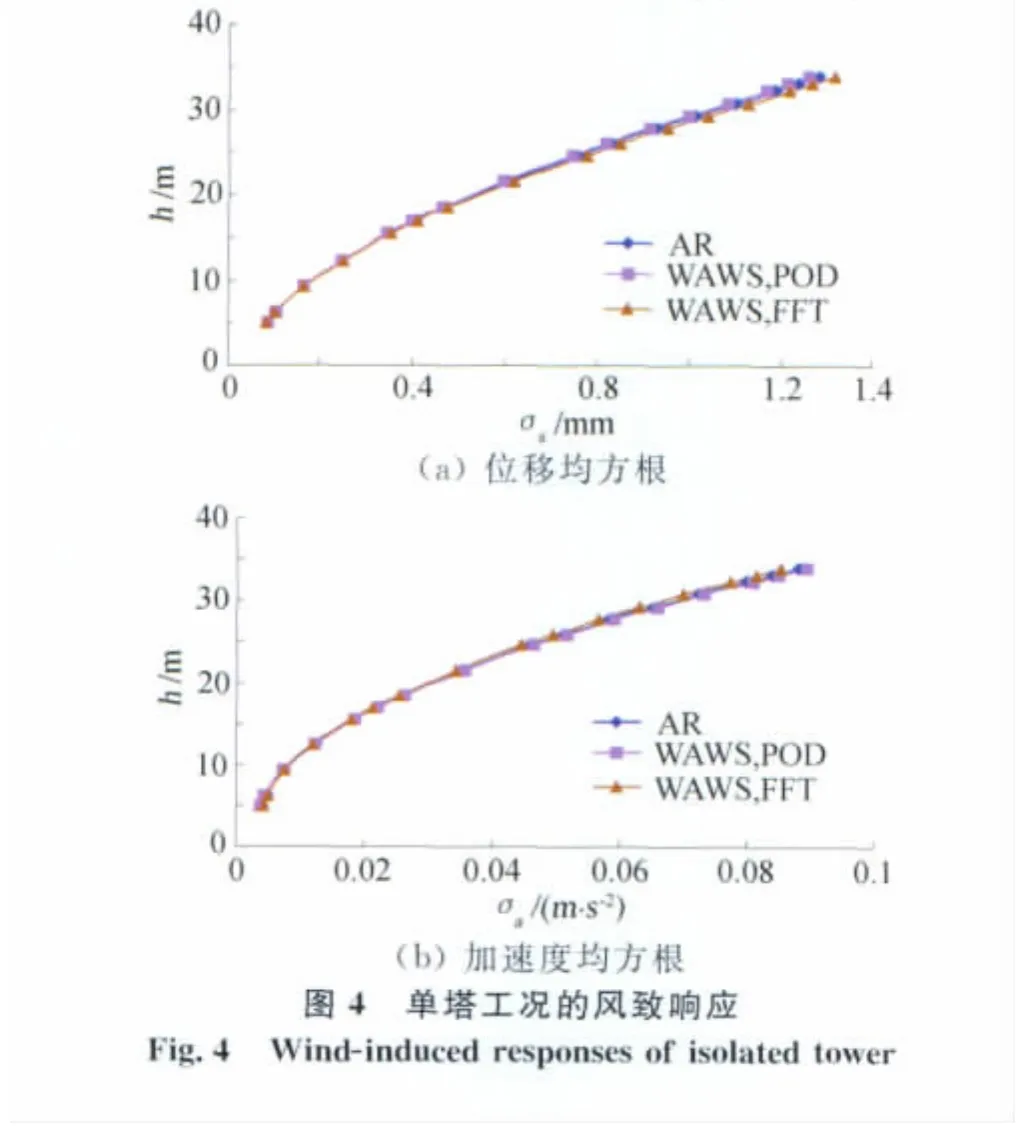
根据三种风场模拟方法得到的风速时程，进行输电塔的风振时域分析，获得输电塔各高度的位移和加速度响应的均方根σs和σa，如图4所示，图中纵坐标的高度h数据对应于输电塔迎风面右侧各层节点，以下各图同。由图4可见三种模拟方法得到的位移和加速度响应基本一致，说明三种模拟方法均可以用来模拟单塔在一维情况下的脉动风场。

3．2 塔线体系情况下的风致响应

对塔线体系的227个点进行风速时程模拟，由于模拟的点数较多，互谱密度矩阵出现不正定情况，无法进行Cholesky分解，则基于FFT变换的WAWS法不能应用。因此塔线体系的风场模拟采用基于POD分解算法的WAWS法和AR法。塔线体系227个节点风速模拟所需的时间见表3，可以发现AR法的效率不如基于POD分解的WAWS法。图5给出基于上述两种模拟方法计算获得的位移和加速度响应均方根，可以发现两种方法的计算结果比较接近，两种方法均适用于塔线体系的脉动风场模拟。

图5 塔线体系工况的风致响应Fig．5 Wind－induced responses of tower line system

3．3 单塔和塔线体系情况的比较

前面2节分别针对单塔和塔线体系的风振响应进行计算，下面以基于POD分解算法的WAWS法计算结果为例，分析单塔和塔线体系响应的差别，如图6所示。由图6可知，对于位移和加速度响应的均方根，塔线体系的结果均比单塔大。在对输电线路进行风振分析时，建议考虑塔线体系情况。

4 基于三维风场模拟的计算结果

上一节的一维风场只考虑了顺风向，而忽略风场在顺风向、横风向和竖直向的相关性，下面为考虑三维风场的计算结果。为了考虑三个方向脉动风速的相关性，S（ω）中的各个元素Sij（ω）为3×3的子矩阵，这样S（ω）为3n×3n矩阵形式：

式中u、v和w分别代表顺风向、横风向和竖直向。

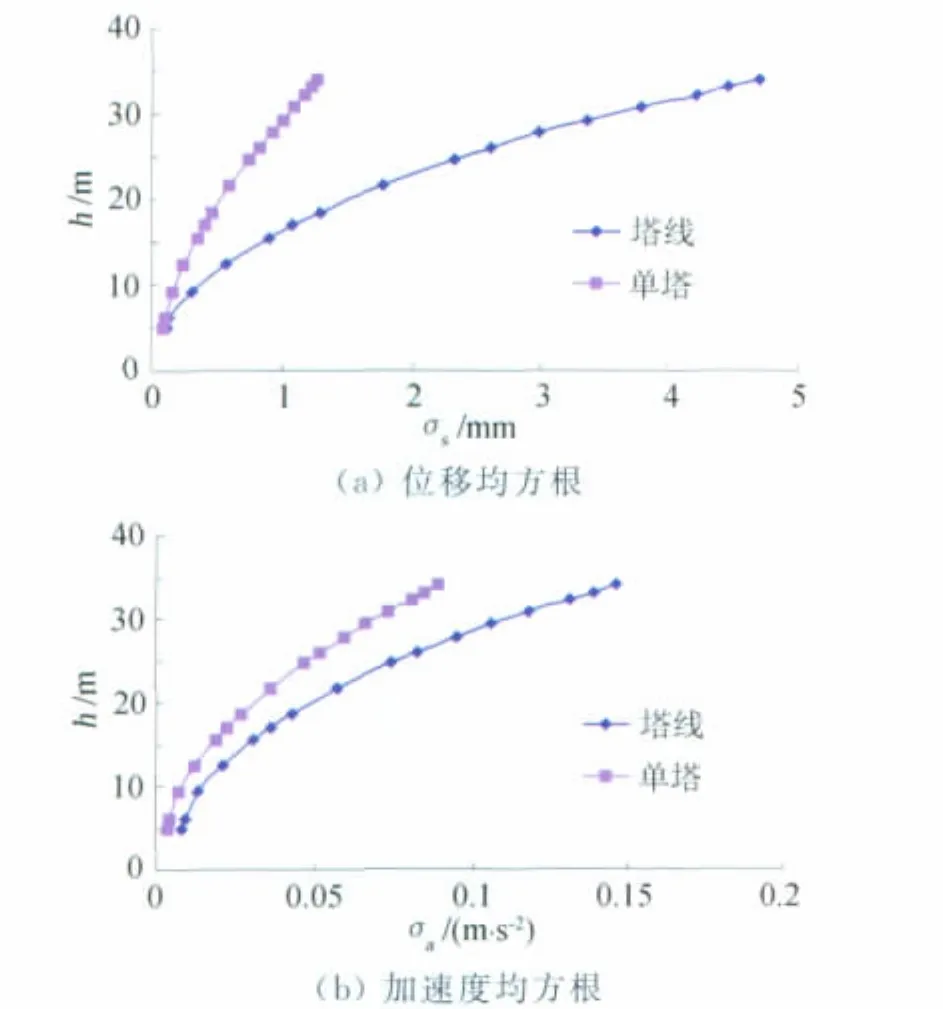
图6 单塔和塔线体系的风致响应结果比较Fig．6 Comparison of wind－induced response of isolated tower and tower line system

本文顺风向风谱采用Davenport谱，竖风向风谱采用Lumley－Panofsky谱：

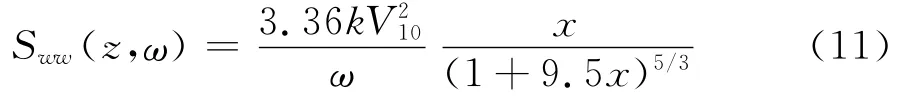
顺风向与竖风向脉动风速的交叉谱如下：

Solari［16］通过大量的实测，认为横风向与顺风向不存在相关性，同时横风向与竖直向也不存在相关性，因此本文不考虑这些相关性。

对单塔的34个模拟点进行考虑三维风场的风速时程模拟，发现无法进行Cholesky分解，则基于FFT变换的WAWS法不能应用。目前关于AR法的模拟理论中还没有给出考虑三个方向相关性的应用。因此采用基于POD分解的WAWS 法，进行考虑三维风场情况下输电塔34个点的脉动风场模拟，模拟所需时间见表3，进行风振计算，并将计算结果与模拟一维风场（WAWS，POD）情况进行比较，如图7所示。

由图7可知，三维风场情况和一维风场相比，位移响应的均方根基本相同，基于三维风场的数据略大；而加速度响应均方根的差别较大，基于三维风场的数据大很多，说明考虑顺风向与其他方向的相关性后顺风向的脉动会更大。对于考虑三维风场后的塔线体系（227个点），基于FFT变换的WAWS 法和AR法均不能应用，而基于POD分解的WAWS法虽然不出错，但经历五天后的计算后仍没有得到模拟结果，已经失去了工程应用价值，在表3中以“非常耗时”来表示。

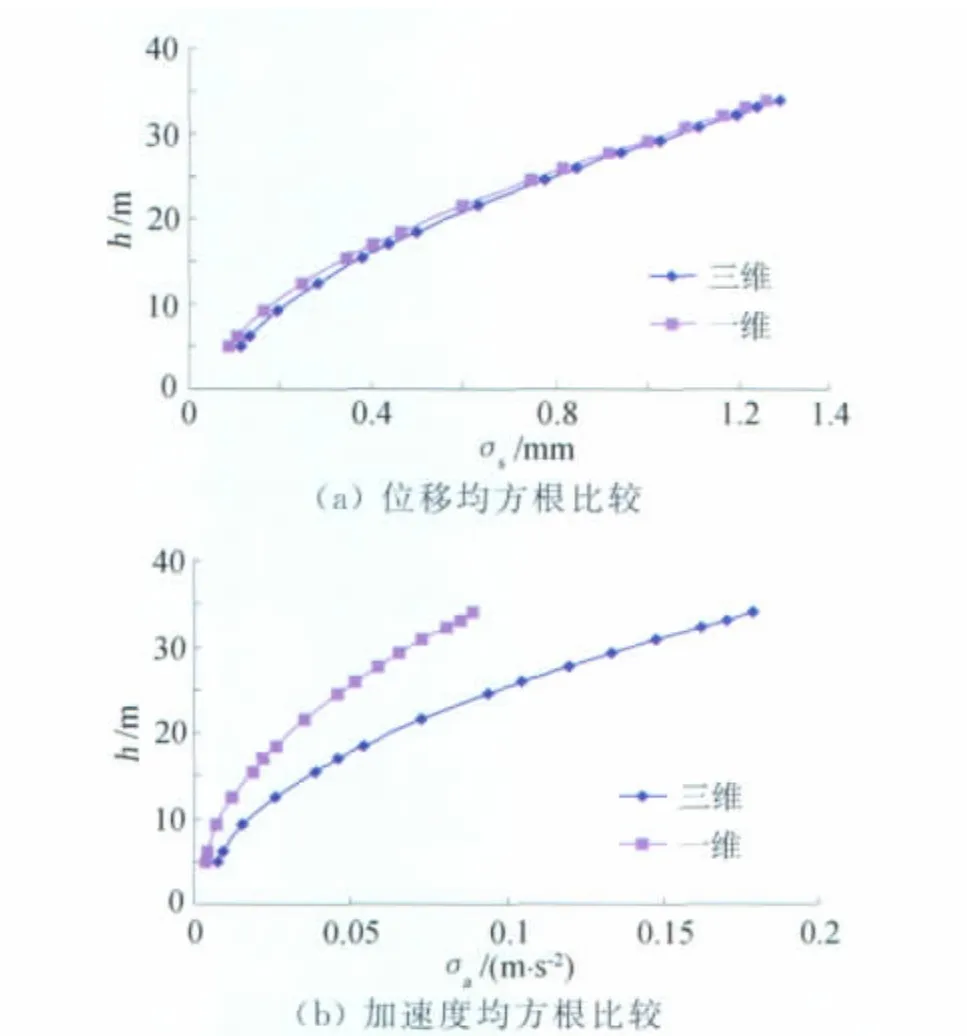
图7 单塔一维和三维风场作用下响应结果比较Fig．7 Comparison of wind－induced responses considering one dimensional and three dimensional wind fields

5 结 论

本文针对脉动风场的模拟方法进行系统分析，并应用到输电塔线体系实例中，有以下主要结论：

（1）针对模拟脉动风场的三种典型方法，当模拟参数相同时，利用模拟出的风速时程进行风振分析的结果基本一致，说明三种方法在脉动风场的模拟原理上都是适用的。

（2）当模拟的点数较多时，风速互谱密度矩阵由于不正定而无法进行Cholesky分解，基于FFT分解的WAWS法不适用，而基于POD分解的WAWS法不存在无法分解的情况，使用截断频率会使计算效率提高很多，具体效率见表3。本文推荐基于POD分解算法的WAWS法，其计算效率高，算法稳定。

（3）计算发现对于位移和加速度响应的均方根，塔线体系的结果均比单塔大，在对输电线路进行风振分析时，应考虑塔线体系情况。

（4）计算发现，考虑三维风场后的位移响应均方根比一维风场略大，而加速度响应均方根大很多，说明考虑顺风向与其他方向的相关性后顺风向的脉动会更大。

［1］ RICE S O．Mathematical analysis of random noise：selected papers on noise and stochastic processes［M］．New York：Dover Publish Inc，1954．

［2］ SHINOZUKA M，JAN C M．Digital simulation of random processes and its application［J］．Journal of Sound and Vibration，1972，25（1）：111－128．

［3］ YANG W W，CHANG T Y P，CHANG C C．An efficient wind field simulation technique for bridges［J］．Journal of Wind Engineering and Industrial Aerodynamics，1997，（67／68）：697－708．

［4］ DEODATIS G．Simulation of ergodic multivariate stochastic processes［J］．Journal of Engineering Mechanics，1996，122（8）：778－787．

［5］ GERCH W，YONEMOTO J．Synthesis of multivariate random vibration systems：a two－stage least squares ARMA model approach［J］．Journal of Sound and Vibration，1977，52（4）：553－565．

［6］ LI Y，KAREEM A．ARMA representation of wind field［J］．Journal of Wind Engineering and Industrial Aerodynamics，1995，121（1）：415－427．

［7］ 曾宪武，韩大建．大跨度桥梁风场模拟方法对比研究［J］．地震工程与工程振动，2004，24（1）：135－140．

［8］ 鲍侃袁，沈国辉，孙炳楠．双曲冷却塔的脉动风荷载模拟和风致响应研究［J］，浙江大学学报（工学版），2010，44（5）：955－961．

［9］ 祝贺．基于AR模型的输电塔结构风荷载模拟技术［J］．吉林电力，2006，34（2）：20－23．

［10］贾瑞庆，杨振伟，代晓光，等．基于时域法的输电塔抗风研究［J］．水电能源科学，2009，27（5）：197－200．

［11］白海峰，李宏男．大跨越输电塔线体系随机脉动风场模拟研究［J］．工程力学，2007，24（7）：146－151．

［12］韩枫，肖正直，李正良．1000KV汉江大跨越输电塔线体系三维脉动风场模拟［J］．高电压技术，2009，35（5）：999－1004．

［13］李黎，胡亮，樊剑，等．具有桥塔风效应的桥梁风场数值模拟［J］．振动与冲击，2007，26（5）：14－18．

［14］沈国辉，袁光辉，楼文娟，等．覆冰脱落对输电塔线体系的动力冲击作用研究［J］．工程力学，2010，27（5）：210－217．

［15］DAVENPORT A G．The dependence of wind load upon meteorological parameters［A］．Proceedings of the International Research Seminar on Wind Effects on Building and Structures［C］，University of Toronto Press，Toronto，1968：19－82．

［16］SOLARI G，PICCARDO G．Probalistic 3－D turbulence modeling for gust buffeting of structures［J］．Probabilistic Engineering Mechanics，2001，16：73－86．