西藏电网暂态稳定分析的动态负荷模型及发电机参数等值

田位平，唐文龙，赵云明

(西藏农牧学院电气工程学院，西藏 林芝 860000)

电力系统数值仿真计算的精确性不仅取决于计算机软件、硬件和算法的发展，更主要取决于各元件的仿真模型和参数的准确性。正确计及负荷模型的作用，不仅可以提高仿真计算的精度，在某些临界情况下还可能改变定性的结论［1］。基于实测负荷数据建立的负荷模型包括:(a)模型结构，包括静态特性、综合负荷、差分方程、考虑配电网支路的综合负荷模型、考虑电源的广义负荷模型等;(b)参数辨识，包括最小二乘、卡尔曼滤波、非线性递推滤波、优化的非线性辨识等。

大量现场实测负荷数据和动态物理仿真模拟数据的辨识结果表明［2］:同一负荷成分在不同扰动情况下的负荷特性数据辨识结果不稳定，有时相差十几倍到百倍，即模型参数存在较大的分散性。而模型结构选择不正确、不真实以及负荷噪声的存在是负荷模型参数分散的主要原因［3］。解决负荷模型参数分散性问题的主要方法为负荷特性综合方法。

由于电力负荷的复杂性、分散性和随机性等特点，建立完全精确的负荷模型是一个难题。因此，要解决电力系统参数辨识问题，关键要解决非线性问题和模型不确定性问题。而人工智能方法中的人工神经网络具有的自适应、自学习、非线性重构等特点，因此可以用人工神经网络法解决电力系统参数辨识问题［4-6］。

在发电机的原动机输入机械功率、惯性时间常数和转子角度初值三者中，以原动机输入机械功率的不确定性对稳定性数值仿真计算结果影响最大，惯性时间常数次之，转子角度初值最小。当取原动机输入机械功率或惯性时间常数为不确定值时，计算结果的不确定性随着仿真时间的推移有不断增大的趋势;而当取转子角度初值为不确定值时这一现象则不明显［7］。

负荷模型不仅对电力系统的暂态稳定和电压稳定有重要影响，也直接影响电网某断面传输功率。在没有精确负荷模型的情况下，往往采用比较保守的负荷模型。采用精确的负荷模型后，对于有些联络线路，可以在系统安全稳定运行的前提下提高电网之间的传输功率，从而提高系统运行的经济性［8］。

在电力系统稳定性数值仿真分析中，除了要考虑精度、机理或非机理模型、计算量和计算速度、参数获取和工程应用背景等因素外，还要结合所研究问题的主要方面选择合适的负荷模型。本文基于西藏电力负荷的特点，分别采用线性前馈网络算法和线性规划方法辨识动态负荷模型参数。为了克服线性前馈网络在极值点附近出现振荡现象，并有较快的神经网络训练计算速度，提出连接权w和学习速率η的取值应满足的条件。

1 广义负荷模型的建立

1.1 广义负荷模型的概念

图1 增广负荷模型Fig.1 Generalized load model

包含有电源但依然以负荷为主的区域被称为广义电力负荷［9］。增广负荷模型(GLM，generalized load models)为等值电动机、等值静态负荷和同步发电机并联组成，模型中考虑了电源的影响，其结构如图1所示。在GLM的基础上，进一步考虑配网的等阻抗和无功补偿的模型为广义负荷模型。

1.2 具有西藏负荷特点的广义实用负荷模型

文献［10］认为，负荷建模的3类测量变量，即发电机相对功角、联络线功率及枢纽节点电压中，发电机相对功角和联络线功率的灵敏度大、辨识精度高，更适合作为负荷建模的测量变量。但由于发电机的相对功角获取较为困难，在建模过程中一般选择联络线功率和节点电压作为测量变量，其中节点电压需要选择灵敏度较高，即电压变化率较大的节点作为观测点。

在西藏电力系统中，电力负荷基本上都接在输电距离为10～15 km的10 kV输电线路上，并且有部分小水电系统通过10 kV线路并入了电力系统，在10 kV配电网中普遍没有装设并联电容补偿装置。西藏电力负荷中感应电动机所占的比例较小，主要是民用和商业负荷。鉴于西藏电力负荷的结构特点，本文在已有增广负荷模型的基础上进行了改进，提出考虑配网等值阻抗、综合性质的等值动态负荷以及等值发电机的暂态计算负荷模型(广义实用负荷模型)，其结构如图2所示。

图2 暂态计算负荷模型Fig.2 Load model for transient stability analysis

该模型的特点是容易获取有关参数，需要辨识的参数较少，其中等值静态负荷和感应电动机用等值动态负荷即差分方程来描述。该模型具有对有功功率和无功功率描述能力强等优点，利用电网中的数据采集和监视控制或故障录波器获得的数据容易辨识差分负荷模型的系数。等值发电机为接入电网的分布式小水电系统经简化等值并折算后的模型。通过对西藏电网的调查和统计，配电线路和配电变压器在等值容量基准下的等值阻抗取为0.045+j 0.110 pu。

模型参数的提取关键是负荷的合理选取，模型合理与否的基本条件是潮流平衡［11］。本文的等值动态负荷潮流平衡关系为

式中:SL——等值动态负荷潮流，其中负荷SL使用二阶差分负荷模型;SG——等值发电机潮流;SS——配电网负荷潮流。

2 差分负荷模型的参数辨识

文献［1］认为，对无隐层的线性前馈网络(LBP，linear back propagation)，当激励函数f(x)为线性函数时，可直接利用线性前馈网络的连接权值与差分负荷模型中系数的对应关系求取参数;讨论了无隐层的线性前馈网络的泛化能力，并对大扰动下的负荷进行建模和仿真，结果显示无隐层的线性前馈网络具有很强的泛化能力。当建模数据的电压和频率变化小，检验或使用数据的电压和频率变化大，这就是外推;反之就是内插［12］。

2.1 线性前馈网络与差分负荷模型的映射关系

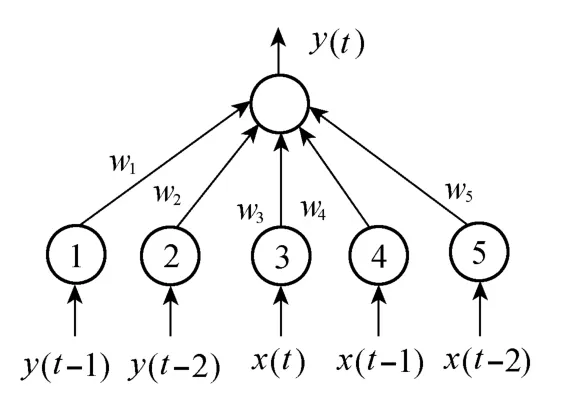
图3 无隐层的线性前馈网络Fig.3 linear back propagation network without hidden layer

无隐层的线性前馈网络如图3所示，则无隐层的线性前馈网络映射关系为

式中:y(t)——无隐层线性前馈网络的输出;y(t-j)，x(ti)——输入层各神经元的输入;wi，wj——输入层至输出层各神经元之间的连接权值。

二阶差分负荷模型(差分方程)为

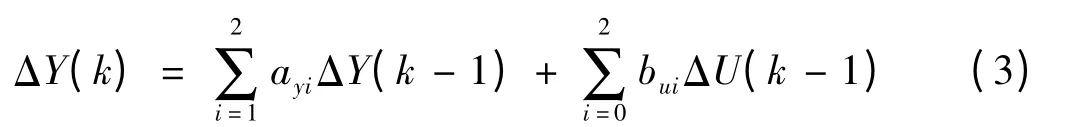
式中:ΔY(k)，ΔY(k-1)——有功或无功的偏差;ΔU(k-1)——电压的偏差;ayi，bui——差分负荷模型系数。

从式(2)和式(3)可以看出，无隐层的线性前馈网络可直接描述差分负荷模型，线性前馈网络的连接权值wj，wi即为差分负荷模型中的ayi，bui值，且差分负荷模型可以描述动态特性负荷。

2.2 无隐层线性前馈网络连接权值辨识算法

设无隐层线性前馈网络的输入层有n个神经元，1个神经元输出，激励函数取f(x)=x，训练集中包含m个样本为(Xp，Yp)，p=1，2，…，m。wi表示神经元输入到输出的连接权，神经元i的输入为xpi，神经网络的实际输出为ypi，学习速率为η，最大容许逼近误差为ε。则无隐层线性前馈网络的输入输出关系为

网络误差为

式中:Ep——网络误差;dpi——神经网络的期望输出。

按照δ学习规则采用梯度最速下降法，即连接权值沿误差函数的负梯度方向改变。若wi的变化量记为Δpwi，则有

对于线性激励函数的δ学习规则，可推导出输出层误差计算式为

则连接权值更新计算式为

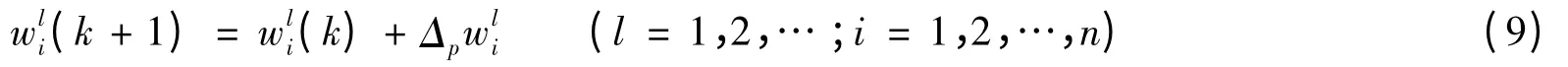
线性前馈网络逼近误差应满足:

2.3 无隐层线性前馈网络的学习训练

在线性前馈网络学习训练过程中，连接权值的初值、学习方式、激励函数、学习速率等对训练过程有较大的影响。该学习训练本质上属于梯度搜索法，从最优化理论可知，不可避免地存在局部极小以及在极值点附近学习速度较慢的问题，有时甚至会在极值点附近出现振荡现象，而不能平滑地趋于最优解，特别是激励函数取为线性函数f(x)=x时，此现象更为突出。

一般情况下，连接权值通常初始化为小的随机值，尽可能覆盖整个权阵的空间域，并避免出现初始权阵系数相同的情况。为了避免在极值点附近出现振荡现象和收敛慢等问题，在已知线性前馈网络输入的情况下，本文提出无隐层的线性前馈网络连接权w和学习速率η的取值应满足:

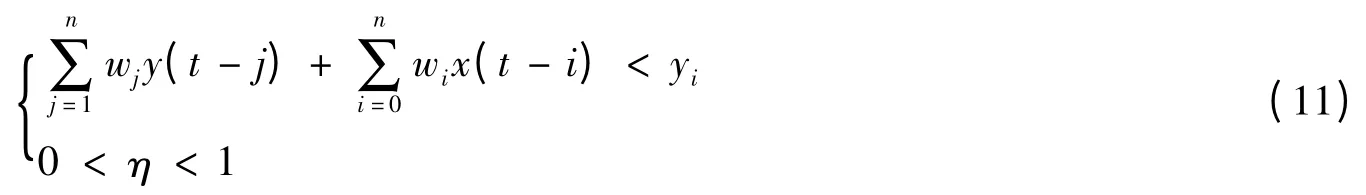
2.4 无隐层线性前馈网络连接权值辨识算法的特点

a.辨识所需参数容易获取，编制的线性前馈网络连接权值辨识算法程序较为简单，输入层的节点数易于增减，且无隐层线性前馈网络连接权值对应于差分负荷模型(差分方程)的系数。

b.w和η在满足式(11)的条件下能较好地避免在极值点附近出现振荡现象和收敛慢等问题，克服了连接权值时变性大的缺点，并利用综合负荷性质的参数(综合负荷的有功、无功、电压等)进行差分负荷模型系数辨识，以解决参数分散性问题。

c.采用无隐层线性前馈网络连接权值辨识算法和线性规划(LP，linear programming)方法分别辨识的差分负荷模型系数，根据负荷输入数据计算的输出响应相差不大，表明两种方法辨识差分负荷模型响应的内插能力较强，外推能力均弱。

采用无隐层线性前馈网络连接权值辨识算法和线性规划方法，对西藏林芝电网10 kV沿嘉线综合负荷性质的差分负荷模型系数进行辨识，结果见表1。表1中，a1，a2为差分负荷模型功率偏差系数，b0，b1，b2为差分负荷模型电压偏差系数。

表1 沿嘉线负荷二阶差分负荷模型参数辨识结果Table 1 Parameter identification results of second-order difference load model for Yanjia Line

3 等值同步发电机的参数

同步发电机是反映系统动态特性的关键元件。从惯量中心理论出发，可以将某一区域的发电机群等效为在惯量中心点处有一台等效的发电机对区域内负荷集中供电［11］。由于接入的小水电系统结构简单，可采用发电机并联等效原理如图4所示。

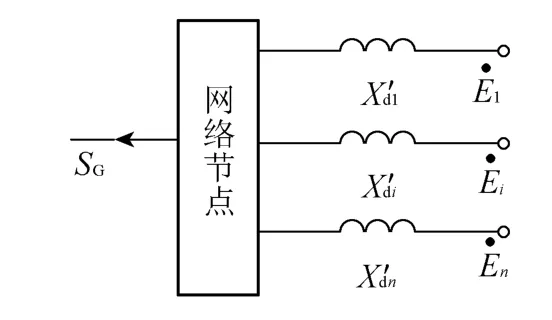
图4 发电机并联等效Fig.4 Parallel equivalent generators

发电机模型采用E″电势恒定模型，为二阶转子运动方程(式(12))。该模型在PSASP中需要的参数较少，仅需x'd，x″d，x2和TJ并且容易获取，但应注意等值发电机各标幺参数的基准值。

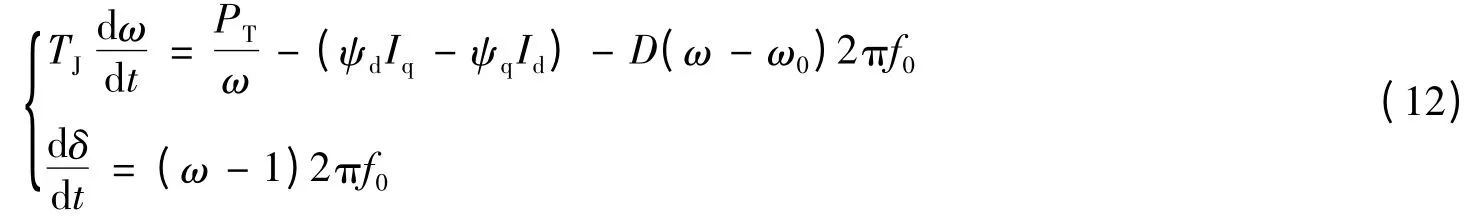
式中:TJ——发电机转子惯性时间常数;ω——角频率;PT——机械功率;ψd，ψq——定子绕组d轴和q轴磁链;Id，Iq——定子绕组d轴和q轴电流;D——阻尼系数;f0——频率;δ——功角;t——时间。

尽管实际系统可能存在多台发电机，但只要发电机基本同步，就可以等效为一台机［9，13］。发电机参数采用加权聚合法进行等值，参数计算为

式中:TJΣ——等值发电机在等值容量基准下的惯性时间常数;X'd——等值发电机在等值容量基准下的直轴暂态电抗。

当等值基准容量为SΣ时，必须将各发电机的额定惯性时间常数和直轴暂态电抗归算为等值基准下的标幺值:

式中:SNi——第i台发电机的额定容量;TJNi——第i台发电机的额定惯性时间常数，x'dNi——第i台发电机额定基准下直轴暂态电抗的标幺值。

应用以上原理，林芝县区域等值同步发电机的模型参数为SΣ=2.250 MVA，xd=1.302 pu，x'd=0.821 pu，x″d=0.231 pu，xq=0.680 pu，x2=0.314 pu，TJΣ=3.444 s。如需要对励磁系统进行参数聚合，则参见文献［14］。

4 广义实用负荷模型暂态计算结果比较

图5 LHZ3-LLL1功角曲线Fig.5 Power-angle curves of LHZ3－LLL1

分别采用配网综合负荷模型和适应西藏电力负荷特点的广义实用负荷模型，在35 kV中心变至新区变联络线上发生三相短路2.5 s切除故障后，仅给出老虎嘴和六零六电厂机组相对功角的暂态稳定计算结果，见图5。

从图5可以看出，采用以上两种模型时发电机相对功角变化趋势一致，仅表现在采用配网综合负荷模型时，故障切除后的功角振荡幅度略大，并主要取决于感应电动机所占的比例。因此，采用综合性质的差分等值动态负荷模型来代替配网综合负荷模型中的等值静态负荷和感应电动机是可行的，算例验证了适应西藏电力负荷特点的广义实用负荷模型结构和参数的有效性及准确性。

5 结 语

提出适合西藏电力负荷特点的广义实用负荷模型，利用无隐层线性前馈网络连接权值与差分负荷模型中系数的对应关系，编制了线性前馈网络的训练算法程序来辨识差分负荷模型系数，用以表征综合性质等效负荷的动态特性，且模型参数求取方便。提出了无隐层线性前馈网络训练连接权值的初值和学习速率选择条件，使无隐层线性前馈网络训练过程中避免了在极值点附近出现振荡现象并具有较快的计算收敛速度。将无隐层线性前馈网络和线性规划方法建立的差分负荷模型的输出响应特性进行对比，结果表明无隐层线性前馈网络的内插能力稍强，两种方法的外推能力均弱。通过工程算例验证了适应西藏电力负荷特点的广义实用负荷模型结构和参数的有效性及准确性。

［1］艾芊，陈陈，沈善德，等.简化前馈网络用于负荷模型参数辨识的研究［J］.中国电机工程学报，2005，25(5):21-27.(AI Qian，CHEN Chen，SHEN Shande，et al.Research on parameter identification of load models by using linear BP networks［J］.Proceedings of the CSEE，2005，25(5):21-27.(in Chinese))

［2］沈善德.电力系统辨识［M］.北京:清华大学出版社，1993.

［3］张红斌，汤涌，李柏青.差分方程负荷模型参数分散性的研究［J］.中国电机工程学报，2006，26(18):1-5.(ZHANG Hongbin，TANG Yong，LI Baiqing.Study on dispersing of difference equation load model parameters［J］.Proceedings of the CSEE，2006，26(18):1-5.(in Chinese))

［4］艾芊.电力系统动态分析人工智能方法［D］.北京:清华大学，1998.

［5］谢开贵，李春燕，周家启.基于神经网络的负荷组合预测模型研究［J］.中国电机工程学报，2002，22(7):85-89.(XIE Kaigui，LI Chunyan，ZHOU Jiaqi.Research of the combination forecasting model for load based on artificial neural network［J］.Proceedings of the CSEE，2002，22(7):85-89.(in Chinese))

［6］KU B Y，THOMASR J，CHIO C Y.Power system dynamic load modeling using artificial neural networks［J］.IEEE Trans on Power Systems，1994，9(4):1868-1874.

［7］王守相，郑志杰.模型参数不确定性对电力系统时域仿真的影响［J］.继电器，2007，35(4):36-39.(WANG Shouxiang，ZHENG Zhijie.Impact of uncertainty of model parameters on power system time domain simulation［J］.Relay，2007，35(4):36-39.(in Chinese))

［8］张景超，鄢安河，张承学，等.电力系统负荷模型研究综述［J］.继电器，2007，35(6):83-88.(ZHANG Jingchao，YAN Anhe，ZHANG Chengxue，et al.Summary of load model research in power system［J］.Relay，2007，35(6):83-88.(in Chinese))

［9］鞠平，何效军，黄丽，等.广义电力负荷的模型结构与参数确定［J］.电力系统自动化，2006，30(23):11-13.(JU Ping，HE Xiaojun，HUANG Li，et al.Model structures and parameter estimation of generalized loads［J］.Automation of Electric Power Systems，2006，30(23):11-13.(in Chinese))

［10］付红军，鞠平，孙冉，等.广域电力系统负荷建模的对比研究［J］.电力系统自动化，2010，34(5):43-47.(FU Hongjun，JU Ping，SUN Ran，et al.Contrast studies on load modeling of wide area power grid［J］.Automation of Electric Power Systems，2010，34(5):43-47.(in Chinese))

［11］汪小明，刘涤尘，吴军，等.电力系统暂态稳定分析广义负荷模型［J］.电网技术，2011，35(3):44-48.(WANG Xiaoming，LIU Dichen，WU Jun，et al.A generalized load model for transient stability analysis of power system［J］.Power System Technology，2011，35(3):44-48.(in Chinese))

［12］贺仁睦，魏孝铭，韩民晓.电力负荷动特性实测建模的外推和内插［J］.中国电机工程学报，1996，16(3):151-154.(HE Renmu，WEI Xiaoming，HAN Minxiao.Power system dynamic load modeling based on the measurements in the field［J］.Proceedings of the CSEE，1996，13(6):151-154.(in Chinese))

［13］汤涌，张红斌，侯俊贤，等.负荷建模的基本原则和方法［J］.电网技术，2007，31(4):1-5.(TANG Yong，ZHANG Hongbin，HOU Junxian，et al.Study on essential principle and methods for load modeling［J］.Power System Technology，2007，31(4):1-5.(in Chinese))

［14］闻丹银，孙黎霞，黄桦，等.电力系统动态等值中励磁系统参数聚合方法对比研究［J］.河海大学学报:自然科学版，2012，40(3):350-356.(WEN Danyin，SUN Lixia，HUANG Hua，et al.Comparative studies on methods for parameter aggregation of excitation system for power system dynamic equivalent［J］.Journal of Hohai University:Natural Sciences，2012，40(3):350-356.(in Chinese))