使用改进的POCS算法的超分辨率图像复原

谢甜

（武汉科技大学 湖北 武汉 430081）

由于受到成像条件和成像因素等方面的影响，在图像获取的过程中不能得到原始场景中的所有信息。光学成像系统相当于一个低通滤波器，由于环境因素的影响，系统响应在某个截至频率上的值都为零。超分辨率图像重建具有重要的应用前景，如：遥感，医学，安全监控，等等。超分辨率图像重建算法可以分为两大类：频域算法和空间算法。空间算法使用一般的观测模型，并具有良好的适应性和重建结果。空间算法是超分辨率重建技术研究的主要方向，其中，POCS算法是的最空间的有前途的算法之一[1-2]。

1 传统POCS算法的基本理论

在超分辨率图像重建过程，首先建立一个图像采集模型，一般的图像采集模型[3]可表示为

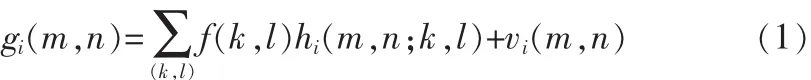
其中，f（k，l）表示理想的高分辨率图像，gi（m，n）表示低分辨率的观察图像序列的第 i帧，hi（m，n；k，l）表示第 i帧图像的 PSF（点扩散函数），PSF 包括模糊和采样，vi（m，n）表示第 i帧图像的加性噪声。

我们定义下面的封闭的，凸约束[4]（在每帧的每个观察到的低分辨率图像的一个像素）

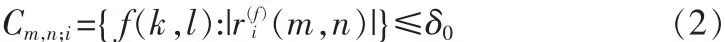
这里

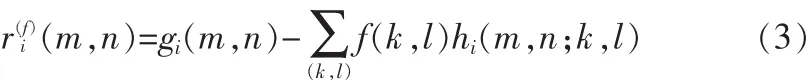
代表的统计不确定性，在观察时其值被设置为等于cσv，其中的噪声的标准方差为σv，并设置统计支撑域为c≥0。

则定义图像上的任意一个投影为

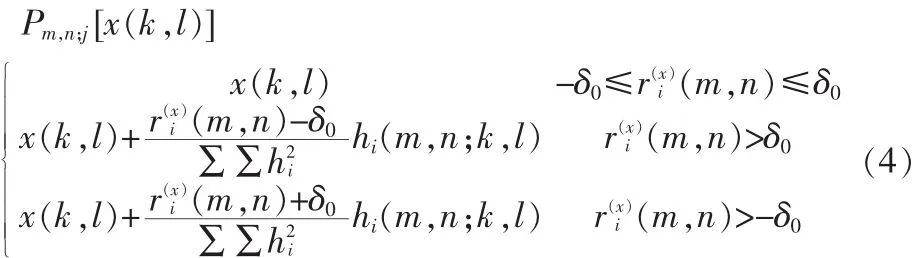
使用POCS算法时，会使复原图像处在暗部区域的周围领域内的像素的颜色变得更暗的，而处在明亮区域的周围领域内的像素的颜色变得更亮，即产生边缘振荡效应[5]。在观察图像的暗部区域的每个边缘像素被投射到当前估计的高分辨率图像，其投影的位置也是在边缘上。PSF覆盖在边缘位置，将会使明亮的彩色像素处在PSF窗口内，使其复原后的值大于实际观测值。而边缘位置上的暗像素的值将被修改为一个较小的值，使得处在暗部区域的边缘像素的颜色变得更暗。与此相反，在明亮的区域的边缘像素的值也将被修改为一个较大的值，使得在明亮的区域的边缘像素的颜色变得更亮。根据上面的分析，我们可以知道，边缘像素，不仅与其自身有关，而且还与其相邻像素相关[6]。

2 改进的POCS算法

在每个边缘像素及其相邻像素中，我们使沿着边缘方向的PSF的系数保持不变，而使处在正交方向上的边缘像素值减小[7]。这样，复原引起的边缘振铃效应将减少，边缘的功能将很好的被保留下来。

文中采用小波变换[8]模极大值的方法来检测图像的边缘。用这种方法，可以检测到丰富的边缘细节和降低噪声的影响，同时，边缘的位置是精确的。该方法包括以下步骤：

1）计算的沿着x轴方向（垂直方向）和y轴（水平方向），在一定规模中的一个两维高斯函数的一阶导数。其结果分别为 ψ1（x，y）和 ψ2（x，y），它们可以被认为具有小波的特性；

2）ψ1（x，y）和 ψ2（x，y）分别与图像进行卷积，其卷积结果分别表示为Gx和Gy；

3）计算每个像素的梯度值和梯度角；

4）把梯度划分为4个方向：水平，垂直，正对角，和负对角线；

5）检查每个像素的梯度值。如果其梯度值在梯度方向上为最大值，则记录其梯度值；否则设置其梯度值为零；

6）查找所记录的梯度值的最大值，并把它归一化。如果一个像素的归一化的梯度值大于某个阈值时，被认为是一个真正的边缘点的像素，如果不是，则它是一个假的边缘点。

我们扩张了边缘检测图像的结构元素，以便获得较丰富的图像边缘。用这种方式，可以更准确地检测边缘像素和其相邻像素。文中选择了一个方形的结构元素如图1所示，假设它的中心像素是所检测到的边缘像素。

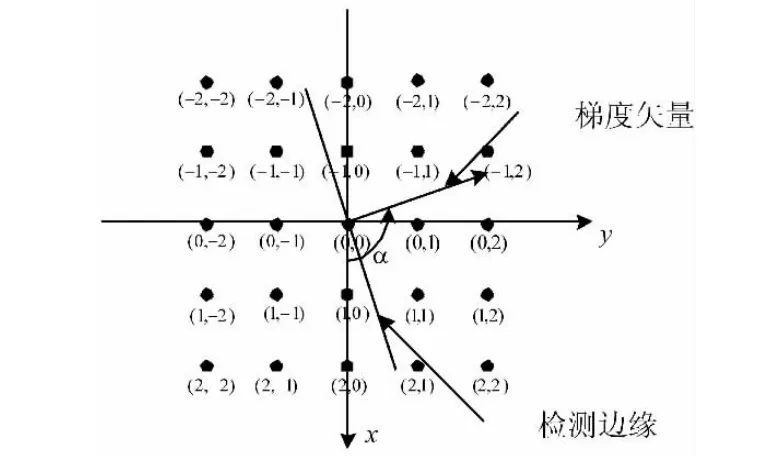
图1 边缘检测图Fig.1 Diagram of edge detection

在图1中设置该结构元素的中心像素坐标是（0，0），其边缘线的斜率是

其中是其中心像素的梯度方向，其值为

其中Gx是沿x方向的中心像素的导数，Gy是沿y方向的中心像素的导数。则最后结果为

则其边缘线的方程式可写为

在任何边缘像素和其相邻象素中，以边缘像素为中心的PSF加权函数，使沿边缘方向的系数保持不变，而离边缘位置越远其相应的PSF的系数系数越小。

假设 PSF 的系数（x，y），d 为（x，y）与边缘线的距离，则为

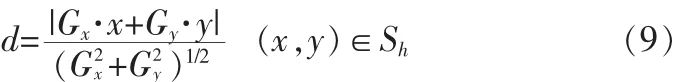
其中Sh表示PSF的支撑域。

为了达到上述的目的，则选择一个指数衰减型的加权函数

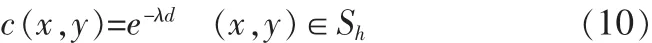
其中是λ一个常数，该值调整函数的下降速度。

则修改后的PSF为：

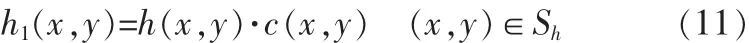
具体地，对于水平方向、垂直方向，正对角和负对角四个方向的边缘函数，如下所示：

最后，h1（x，y）进行归一化，表达式为：

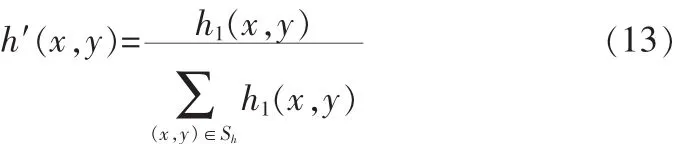
因此，对于每个边缘像素及其相邻像素中，我们使用修改后的PSF公式（12），进行图像复原，但对其它像素我们则使用原始的PSF公式（4），进行图像复原。

3 实验结果

在实验中，一个测试的高分辨率的图像的大小为256×256（如图2所示），将高分辨率图像进行模糊处理，选取标准差为1.5，大小为9×9的高斯模糊；再将模糊图像添加均值为0，标准差为0.1的高斯白噪声得到待复原的低分辨率图像。图3显示的是使用分形插值得到的结果。图4是使用传统的POCS算法得到的高分辨率图像，图5是其局部放大的图像。图6是使用我们的方法得到的高分辨率图像，图7是其局部放大的图像。

从图像中我们可以看到，传统的POCS算法得到的超分辨率图像产生了很多的振铃效应。使用我们的方法明显的减少了振铃效应，得到了比较理想的实验结果。

图2 高分辨率图像Fig.2 High-resolution image

图3 双线性插值Fig.3 Bilinear interpolation

图4 传统的POCS算法Fig.4 Traditional POCS algorithm

图5 图4的局部放大图Fig.5 Local image zooming of Fig.4

图6 我们的算法Fig.6 Our method

图7 图6的局部放大图Fig.7 Local image zooming of Fig.6

4 结 论

文中是研究了基于改进POCS算法的超分辨率图像重建技术。传统的POCS算法会产生边缘振荡效应。本文提出了一种改进的POCS算法，以减少复原图像的边缘振荡效应。从实验结果中可以看出改进的POCS算法和传统的POCS算法相比，明显的较少了在图像超分辨率复原过程中产生的边缘振荡效应。

[1]Youla D C，Webb H.Image restoration by the method of convex projections[J].IEEE Transactions on Medical Imaging，1982，10（1）:81-94.

[2]Sezan M I，Stark H.Image restoration by the method of convex projections[J].IEEE Transactions on Medical Imaging，1982，10（2）:95-101.

[3]Elad M，Feuer A.Restoration of a single superresolution imagefrom several blurred， noisy， and undersampled measured images[J].IEEE Transactions on Image Processing，1997，6（12）:1646-1658.

[4]Mural T A，Ozkan M K，Sezan M I.High-resolution image reconstruction from lower-resolution image sequences and space-varying image restoration[J]. IEEE International Conference on Acoustics， Speech， and Signal Processing，1992，3（1）:169-172.

[5]Patti A J，Altunbasak Y.Artifact reduction for set theoretic super resolution image reconstruction with edge adaptive constraints and higher-order interpolants[J].IEEE Transactions on Image Processing，2001，10（1）:179-186.

[6]卓力，王素玉，李晓光.图像/视频的超分辨率复原[M].北京:人民邮电出版社，2011.

[7]Gozalez R C，Woods R E.数字图像处理[M].阮秋琦，阮余智，译.北京：电子工业出版社，2007.

[8]缑新科，王娜娜.基于多尺度小波变换的变步长LMS滤波算法[J].工业仪表与自动化装置，2012（3）：5-9，13.

GOU Xin-ke，WANG Na-na.An adaptive LMS algorithm with variable step based on multi-scale wavelet transform[J].Industrial Instrumentation&Automation，2012（3）：5-9,13.