基于RBF神经网络的土壤侵蚀预测模型研究

伊燕平，卢文喜，许晓鸿，洪德法

（1．吉林大学 环境与资源学院，长春130021；2．吉林省水土保持科学研究院，长春130033；3．长春市城乡规划设计研究院，长春130021）

目前，土壤侵蚀已成为危害人类生存与发展的主要生态环境问题之一。土壤侵蚀预测模型是实施水土流失监测、指导水土保持措施配置、优化水土资源利用的有效工具，已成为土壤侵蚀学科的前沿领域和土壤侵蚀过程定量研究的重要手段［1］。随着计算机等相关学科的快速发展和土壤侵蚀机理研究的不断深入，自20世纪60年代以来，土壤侵蚀模型研究和模拟技术越来越受到国内外学者的重视，并对此进行了大量研究建立了一系列经验统计模型［2－3］。1965年Wischmeier和Smith在对美国东部地区30个州10 000多个径流小区近30a观测资料的基础上提出了著名的通用土壤流失方程（USLE）［4－5］，并于1978年针对其应用中存在的问题修正了通用土壤流失方程（RUSLE）［6］。与此同时，在土壤侵蚀机理研究方面以美国的 WEPP预测模型［7］、欧洲的EUROSEM模型［8］、澳大利亚的 GUEST模型［9］最具代表性。以上模型复杂性及适用性各异，模型中经验参数适用范围有限，不具备一定的通用性［10］。

人工神经网络是20世纪80年代兴起的一种处理复杂非线性问题的手段，具有自组织、自学习、自适应等特点，不仅被广泛应用于模式识别、图像处理、非线性系统识别等领域，还被广泛用于模拟预测和优化配置等方面［11］。与经验统计模型相比，神经网络模型具有更好的持久性与预测性，能够用于解决同时存在多个自变量和多个因变量的预报问题。土壤侵蚀受多种随机性、模糊性和灰色性等不确定性因素的影响，是一个复杂的非线性系统。针对土壤侵蚀过程的非线性、随机性、模糊性等特点［12］，国内外已有学者将神经网络模型应用到土壤侵蚀预测研究中，如：Licznar等［13］通过神经网络模型对土壤侵蚀的产流产沙过程进行模拟，模拟结果较WEPP模型更准确；赵西宁等［14］应用BP神经网络模型对土壤侵蚀产沙量进行预测，认为神经网络模型比回归模型能更好地刻画出复杂的产沙过程；张科利等［15］应用神经网络模型对土壤侵蚀进行了预报研究。目前大多数神经网络土壤侵蚀预测模型采用BP（Back Propagation）网络，但BP神经网络存在收敛速度慢、局部极小、网络的隐含层节点数难于确定，训练结果过于依赖初始值等缺陷［16－17］。本文在分析径向基函数（RBF）网络基本原理的基础上，以东辽县杏木小流域为研究对象，引入RBF神经网络模型这一新的定量研究方法进行土壤侵蚀预测研究。通过该模型的模拟与预测以期为复杂的土壤侵蚀规律研究提供新的路径，为水土流失综合治理奠定科学基础。

1 RBF神经网络的基本原理

径向基函数（Radial Basis Function，RBF）神经网络是一种局部逼近的前馈式神经网络。它由输入层、隐含层和输出层组成，隐含层采用径向基函数作为激励函数。选用合适的径向基函数是网络得以实现的关键。径向基函数是局部分布、中心径向对称的、非负衰减的非线性函数，它的两个参数（基中心和基宽度）将决定对输入产生显著响应的范围［18－19］。

高斯函数常被作为RBF网络的径向基函数，它的基本表达形式如下：

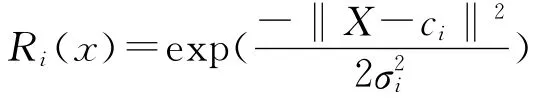
式中：Ri（x）——隐含层第i个节点的输出，i＝1，2，…，m；σi——隐含层第i个节点的方差，它决定着基函数围绕中心点的宽度。

径向基函数将径向基层的每个神经元j（j＝1，2，…，R）的权值向量wj与第p个输入向量xp之间的向量距离与偏差bj的乘积作为输入值，输入表达式：

则径向基层神经元j的输出为：

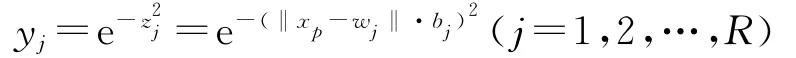
如图1所示。

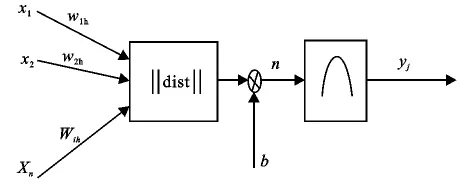
图1 RBF神经网络隐含层神经元的输入与输出示意图

在RBF神经网络训练过程中，隐含层神经元数的确定是一个关键问题，在输入矢量很多时，从0个神经元开始训练，通过检查输出误差使网络自动增加神经元，每次循环使用，使网络产生最大误差所对应的输入矢量作为权值向量，产生一个新的隐含层神经元，然后检查新网络的误差，重复此过程直到达到误差要求或最大隐含层神经元数为止。可见，RBF神经网络具有结构自适应确定、输出与初始权值无关的特点。

2 土壤侵蚀预测模型的建立

2．1 研究区概况

本研究以吉林省东辽县杏木小流域作为研究对象，位于东经125°22′40″—125°26′10″，北纬42°58′05″—43°01′40″。杏木小流域地处长白山余脉，东辽河流域上游，属于典型的低山丘陵区，最高海拔452m，相对高差133m。土壤类型以棕壤土为主，土层厚度为30～70cm，土壤容重为1．58g／cm3。属于寒温带半湿润大陆性季风气候，多年平均气温5．2℃，多年平均降雨量658．10mm。据辽源市水文站50a的观测资料，最大年降水量为911．0mm，最小降水量为410．6mm。最大一日降水量为165．6mm，平均径流系数为0．23。多年平均侵蚀模数为3 350t／（km2·a）。

2．2 数据处理

选取土壤侵蚀的影响因子：汛期降雨量、平均径流系数、土壤容重、有机质含量、孔隙度作为预测模型的输入变量，输出变量为年土壤侵蚀模数，RBF神经网络模型将土壤侵蚀预测问题转化为影响因子和年侵蚀模数的非线性问题。以20组实测数据作为模型的训练样本集，5组样本作为模型的检验样本。在模型学习训练过程中，为了消除各个因子由于量纲和单位不同所产生的影响，首先对其输入输出样本分别进行归一化处理（表1）。

2．3 RBF神经网络模型的训练与检验

RBF神经网络模型输入层神经元数为土壤侵蚀因子数，输入层神经元个数为5，输出层神经元个数为1，调用matlab平台中的函数newrb（）训练网络，自动确定隐含层单元数。网络训练程度与误差控制有关，由表2可见，当均方误差为0．002时，所得网络训练最佳，此时，网络对20组训练样本的拟合误差最大值为1．84%，对5组测试样本的相对误差最大值为3%，误差可控制在5%以内，可见RBF神经网络模型能够达到土壤侵蚀预测的目的（表3）。

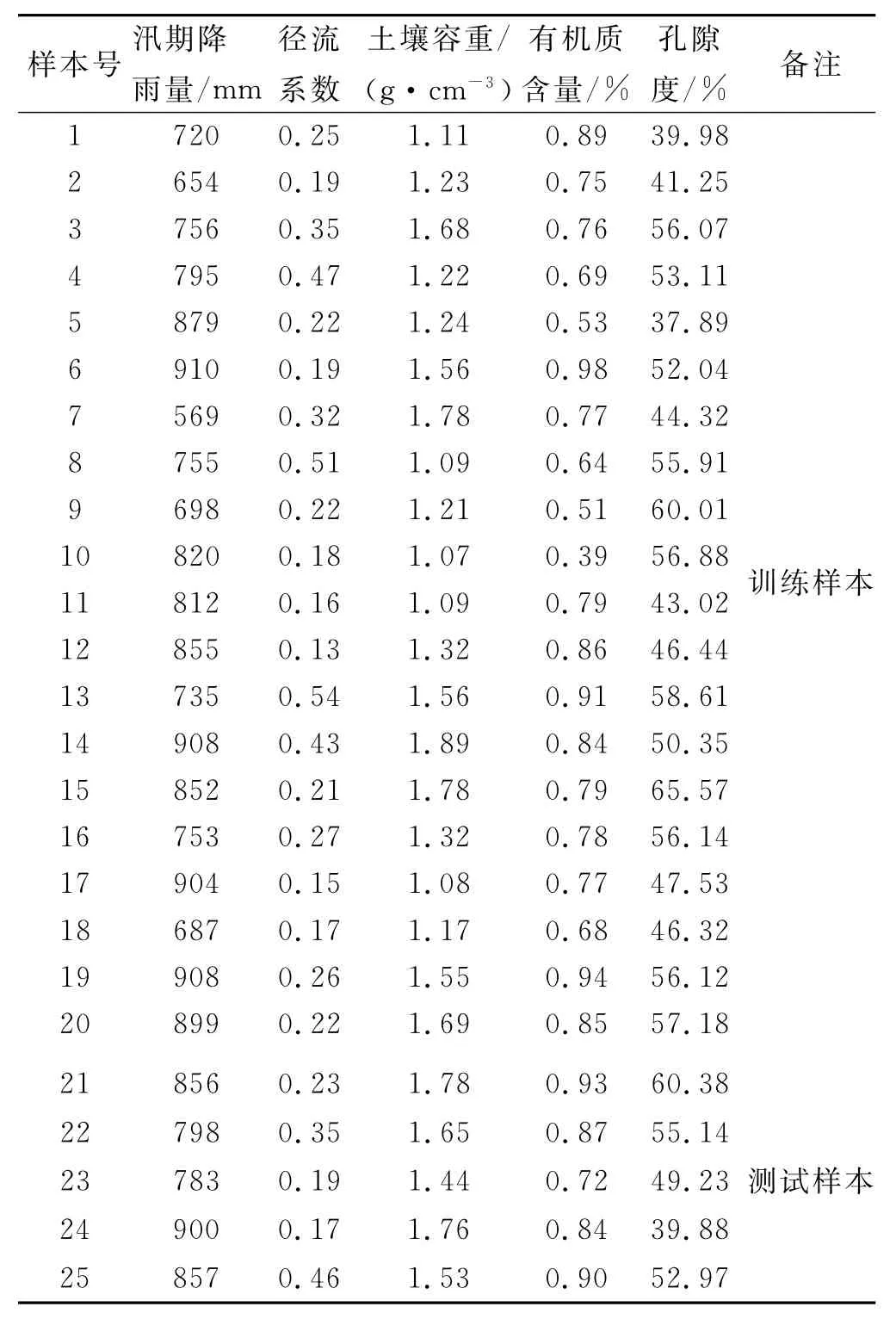
表1 RBF神经网络训练样本与测试样本数据

表2 RBF神经网络训练与检验

3 预测精度分析

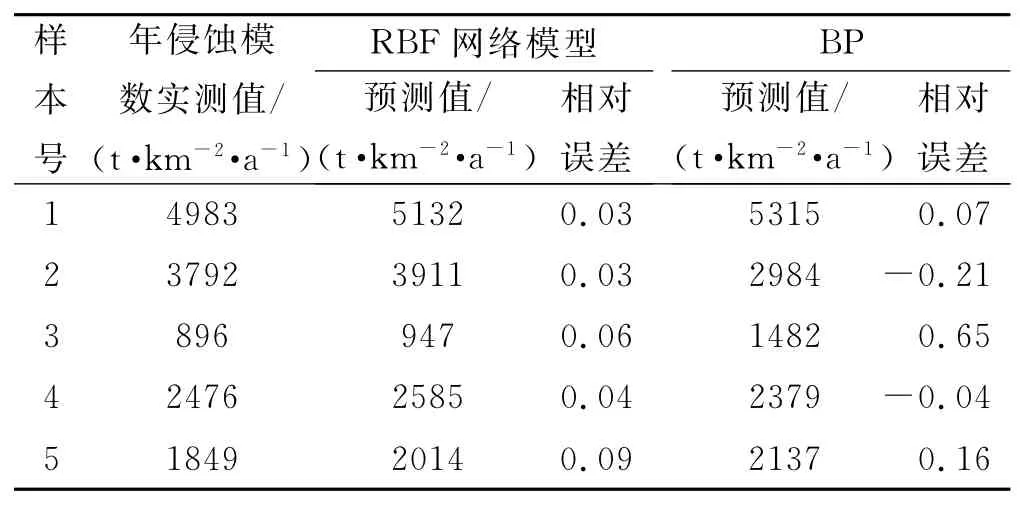
表3 两种预测模型的输出值与实测值拟合结果对比

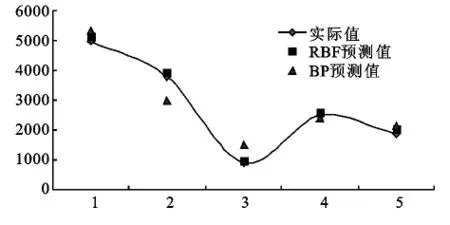
图2 RBF网络模型与BP网络模型对比

表4 RBF网络与BP网络预测误差比较

如表4所示，经计算，RBF神经网络预测模型与BP神经网络相比，RBF神经网络模型得到的预测结果与实测值误差更小，预测精度高于BP神经网络模型。

4 结 论

基于土壤侵蚀过程的复杂性和非线性，本文将RBF神经网络方法引入土壤侵蚀预测中，使土壤侵蚀预测问题转化为影响因子和侵蚀模数的非线性问题，结果显示，RBF神经网络模型的泛化能力较强，可以达到理想的土壤侵蚀预测效果，预测精度较高，具有较大的实用价值，是一种值得推广的土壤侵蚀预测模型。RBF神经网络模型的构建与预测为复杂的土壤侵蚀规律研究提供了新途径。

RBF神经网络模型本身仍处于初步发展阶段，其理论和学习算法还有很多未完善的地方，如没能力解释模型本身的预测过程和预测依据，把问题的特征转变为数字对其结果丢失信息如何处理等，仍需要今后进一步改进和深入研究。

［1］ 张光辉．土壤侵蚀模型研究现状与展望［J］．水科学进展，2002，13（3）：389－396．

［2］ 李发鹏，李景玉，徐宗学．东北黑土区土壤退化及水土流失研究现状［J］．水土保持研究，2006，13（3）：50－54．

［3］ 尹怀宁，汤姿，吕芳．东北平原西部近百年来生态环境退化机制分析［J］．水土保持研究，2003，10（4）：190－192．

［4］ Smith D D．Interpretation of soil conservation data for field use［J］．Agricultural Engineering，1941，22：173－175．

［5］ Wischmeier W H，Smith D D．Predicting Rainfall－Erosion Losses from Cropland East of the Rocky Mountains［M］．USDA Agricultural Handbook，No．292，1965．

［6］ Wischmeier W H，Smith D D．Predicting Rainfall－Erosion Losses［M］．USDA Handbook，No．537，1978．

［7］ Nearing M A，Lane L J，Alberts E E，et al．Prediction technology for soil erosion by water：status and research needs［J］．Soil Sci．Soc．Am．J．，1990，54（6）：1702－1711．

［8］ Morgan R．The European Soil Erosion Model：An Update on Its Structure and Research Base［M］／／Rickson R．Conserving Soil Resources：European perspectives［M］．CAB International，Cambridge，1994．

［9］ Rose C W，Williams J R，Sander C C，et al．A mathematical model of soil erosion and deposition processes：theory for a plane land element［J］．Soil Sci Soc Am J．，1983，47（5）：991－995．

［10］ 符素华，张卫国，刘宝元，等．北京山区小流域土壤侵蚀模型［J］．水土保持研究，2001，8（4）：114－120．

［11］ 张坤，丁新新，洪伟，等．BP神经网络在降雨侵蚀力预测预报中的应用研究［J］．2009，16（1）：53－56．

［12］ 徐鼎甲．用离散微分动态规划制订梯级水电站最优日运行方式［J］．水利水电技术，1996（2）：33－38．

［13］ Licznar P，Nearing M A．Artificial neural networks of soil erosion and runoff prediction at the plot scale［J］．Catena，2003，51（2）：89－114．

［14］ 赵西宁，吴普特，冯浩，等．坡面土壤侵蚀产沙的神经网络模拟［J］．土壤学报，2006，43（2）：324－327．

［15］ 张科利，彭文英，杨红丽．中国土壤可蚀性值及其估算［J］．土壤学报，2007，44（1）：7－13．

［16］ 毛典辉，曾致远，王乘，等．基于支持向量机的土壤侵蚀预测模型研究［J］．人民长江，2007，38（8）：82－84．

［17］ 陈玉红．RBF网络在时间序列预测中的应用研究［D］．哈尔滨：哈尔滨工程大学，2009．

［18］ 柴杰，江青茵，曾志凯．RBF神经网络的函数逼近能力及其算法［J］．模式识别与人工智能，2005，15（3）：310－316．

［19］ 张淮清，俞集辉．波导本征问题分析的径向基函数方法［J］．电子学报，2008，36（12）：2433－2438．

［20］ 朱树先，张仁杰．BP和RBF神经网络在人脸识别中的比较［J］．仪器仪表学报，2007，28（2）：375－379．

［21］ 尹江红，叶汉民，罗明，等．BP网络和RBF网络用于输电线路故障定位比较［J］．中国电力教育，2010，33（184）：259－262．

［22］ 谌爱文．基于BP和RBF神经网络的数据预测方法研究［D］．长沙：中南大学，2007．