基于单层小波变换的加权压缩感知图像处理

王 晨， 高美凤

(江南大学轻工过程先进控制教育部重点实验室，江苏无锡214122)

信号通过抽样由模拟信号转变为数字信号。为了预防信号畸变，传统的抽样以奈奎斯特采用定理为理论基础。该定理指出:为了保证能够完全恢复原信号，采样速率必须大于等于信号带宽的两倍，否则信号频谱会出现混叠，不能准确地恢复原信号。随着现代信息量日益增长的需求，该定理则表现出越来越明显的限制。一方面，随着信号带宽的增加，要求采样速率和处理速度也要相应提高，这样会提高产品实现难度和成本;另一方面，在传统的图像或信号传输过程中，有效的数据往往只有一小部分，大部分采集数据会被舍弃，这样造成了资源浪费而且效率低下。

近些年来，一种新的采样理论——压缩感知［1］被广泛关注。它利用其他变换空间描述信号，使得在保证信息不损失的情况下，用远低于采样定理要求的速率在采样信号的同时，又可完全恢复信号，即将对信号的采样转变为对信息的采样。压缩感知突破了奈奎斯特采样定理的限制，如果信号在某变换域中是稀疏的，并且其稀疏变换与观测系统不相关，那么对信号无失真的采样可通过优化求解一个稀疏变换与观测矩阵构成的欠定方程来完成，因而可以从低分辨率观测中恢复信号，大大提高了信息处理速度。随着压缩传感的深入研究和广泛应用，信息处理领域正不断得到较快发展［2］。

1 压缩感知

压缩感知理论指出，当信号在某组基或者字典下是可压缩或者稀疏的，那么就可以用一个与该基或字典不相关的观测矩阵将信号线性投影为低维观测值，其保留了重建信号所需要的重要信息，通过进一步求解稀疏最优化问题就能从线性观测中精确地重构原始信号。

压缩感知理论框架如图1所示:第1步为信号稀疏表示问题;第2步为信号的线性投影问题，设计一个与正交变换基Φ不相关的M×N维的观测矩阵Ψ，保证原始信号从维降维到M维时重要信息不丢失;第3步为信号重构问题，设计重构算法保证从M维线性观测向量中能够重建原始信号。

图1 CS理论框架Fig.1 Graph of CS theoretic framework

压缩感知是利用信号具有稀疏性表示的先验知识，由观测获得少量的观测值来进行信号重构。考虑长度为N的信号，将其看作RN中N×1的列向量，RN中的任意信号都可由一组N×1的矢量基或，那么信号X可以表示为

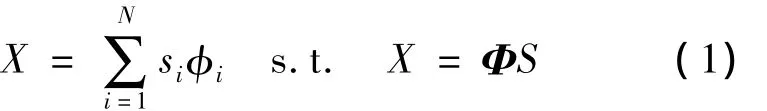
其中S=(s1，…，sN)T为信号在Φ域中的表示，若S的非零分量的个数为K(M≪N)，称S为K-稀疏的。衡量信号稀疏度常用的指标有:(1)0范数，即信号中非零元素的个数;(2)稀疏因子，即信号中非零元素的个数与元素总数的比值;(3)非线性逼近误差，即用正交基Ψ表示信号时的稀疏程度或分解系数的能量集中程度。常用的稀疏基有DCT基、小波基、Gabor基及冗余字典等。

测量矩阵的设计是压缩感知理论的一个重要前提和条件，既要减少压缩测量次数又要确保信号的重建精度。Candès［3］等人指出，如果要精确重构K阶稀疏信号 X，测量次数 M需要满足 M=O(Kln(N))，并且测量矩阵Ψ必须满足约束等距性质(Restrcited Isometry Property，RIP)。高斯随机矩阵的优点是它几乎与任意稀疏信号都不相关，因此，当测量矩阵是高斯随机矩阵时，测量矩阵能以较大概率满足RIP，因此可以通过选择M×N的高斯测量矩阵得到所需的观测矩阵

给定测量矩阵ΨM×N(M≪N)，对信号X观测过程如下:

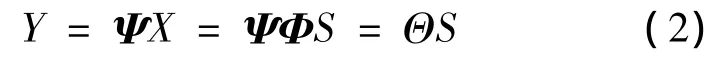
式中，Y为经过观测后获得的观测值，包含了重构原始信号的足够信息;=为M×N矩阵，称为传感矩阵。由方程(2)看出，压缩感知将信号X从N维降到M维观测信号Y，由于观测数量M远小于信号长度N，所以方程(2)是个欠定线性方程组，存在无穷多解;同时由于S为K稀疏的，则可以通过系数分解算法求解式(2)的逆问题得到稀释系数S，再通过式(1)重构得到信号X。Tao［2］等指出当传感矩阵Θ满足约束等距性质RIP时，式(2)中的S可以通过L0的问题求解:

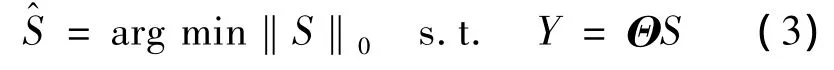
显然L0为NP难的非凸优化问题，Donoho，Chen和Saundrers指出求解更加简单的L1优化问题会得到相同的解:

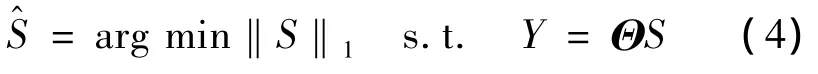
这一简单的改变使问题变成了凸优化问题，可简化为线性规划问题求解。目前有多种求解该问题的算法，典型重构算法分为两类:(1)贪婪追踪算法:匹配追踪(MP)［4］、正交匹配追踪 (OMP)［5］、分段OMP(Stomp)［6］、正则化 OMP(Romp)［7］;(2)凸松弛法:基追踪(BP)［8］、内点法［9］、迭代阈值法［10］、共轭梯度投影法［11］等。

2 基于单层小波变换改进的压缩感知图像重构

2.1 单层小波变换稀疏分解

压缩感知系统中，图像的稀疏表示是实现压缩感知的前提条件，目前普遍使用的的稀疏变换主要有正交变换稀疏表示和冗余字典稀疏分解［12］，其中正交变换构造简单而且实现速度快，其中离散小波变换(DWT)进行稀疏变换用的最为广泛。在原有的压缩感知图像处理中，将原图像首先进行某种变换如DWT，然后构造测量矩阵Ψ，利用该矩阵对小波变换后的稀疏系数进行测量，得到M×N的测量系数，最后利用恢复算法通过得到的测量系数恢复原图像。

小波分解将原图像分解为低频子带和高频子带，高频子带可以认为是稀疏的，而低频子带是原图像在不同尺度下的逼近信号，不能认为是稀疏的。如果将高低频一起测量就破坏了低频分量系数间的相关性，从而重构效果不佳。在压缩感知重构算法中小波分解层数对图像重构有着重大的影响，分解层数越多重构效果越好，大小为256×256，一般分解层数在4层以上。

文献［13］提出了基于单层小波变换的压缩感知改进算法。根据小波分解图像高低频的特点，利用小波变换对原图像进行单层变换，对第一层高频子带进行测量，对低频逼近子带直接观测，这样可以减少重构图像所需的数据量，加强重构的效果。实现步骤如下:

1)对原图像进行一层小波分解得到{LL1，HL1，LH1，HH1}小波子带系数。

2)构造测量矩阵 Ψ 对 LH1，HL1，HH1进行测量，低频LL1直接观测。

3)利用OMP分别对高频稀疏进行重构并与低频子带系数一起进行小波反变换得到恢复图像。

2.2 加权矩阵对小波分解稀疏增强

信号的稀疏程度决定了信号的重构质量和精度，因此对信号进行有效的稀疏表示意义重大，它直接关系到压缩感知的重构精度。简单的稀疏正交变换虽然速度很快，但信号在此变换域下的稀疏性不高。因为当信号特征与稀疏变换的原子特征一致时能够有效地得到信号精确的表示，但由于固定基不一定能灵活表示自然信号，因而在此稀疏域下不能够足够稀疏，则大大影响了压缩感知的性能。对于文中所用的简单正交变换离散小波变换而言，它仅仅沿着图像的水平和垂直两个方向进行变换。在图像灰度渐变区域对于图像的稀疏表示效果很好，经量化后高频子带产生大量的零系数;但在非平滑区域，高频子带却保留有较多的大幅度系数，满足不了稀疏性的要求。因此，文中在此基础上提出了一种增强其稀疏度的改进方法。

二维离散小波对图像进行单层变换后保留低频系数，高频的稀疏系数S中除了有L个大系数，其他S～L个系数并不全为零，而有些是接近于零，不是绝对稀疏即不能足够稀疏。为了使得高频系数更加接近于绝对稀疏，文中提出引入加权矩阵的改进方法。引入加权矩阵A，首先A是对角矩阵，且矩阵中系数

其中阈值系数λ为稀疏系数中选取的某一个系数的绝对值，加权系数设置的原则为使得稀疏系数中的大系数尽量保持不变而小系数尽量趋向于零［14］，即ai∝Si，加权系数矩阵左乘S得0，所以说当p→+∞时，S中原本接近零的小系数右乘加权矩阵后变为零，因此，S'比S稀疏性更好，即引入加权矩阵后稀疏系数更加接近于绝对稀疏。

在对3个高频子带的观测过程中引入加权矩阵增强其稀疏度，则压缩感知的数学模型为

式中A为引入的对角加权矩阵，其中加权系数{a1a2…an}在主对角线上而其他位置为0，相应的压缩感知重构数学模型则变为

可将式(6)变换为

其中B=A－1，S'=AS。B矩阵也为对角矩阵B=diag{b1，b2，…，bn}且bi=，由此可知式(7)的最优解即为式(8)的最优解，即原图像可以由重构S'得到。

由此引入加权矩阵后可以使信号分解后的稀疏性进一步加强，即将L个大系数保留，而剩余小系数变得更小，从而更接近理想的绝对稀疏，所以引入加权矩阵后3个高频子带的系数矩阵的稀疏性更好。

2.3 基于单层小波变换稀疏分解改进与重构

利用单层小波稀疏分解和加权系数矩阵的特点，通过单层小波变换获得图像高低频子带，保留低频部分，对高频系数进行加权处理。

由上文提到重构问题为NP难问题时，传感矩阵必须满足RIP特性，应用加权系数矩阵后，传感矩阵ΨΦ =Θ变为了ΨΦA－1=Λ。由于加权系数矩阵仅仅使Θ中某些列向量的模的大小发生改变，而向量内部结构并未发生改变，稀疏度也未发生改变。所以，如果原先稀疏矩阵与观测矩阵不相关，则左乘加权系数矩阵后同样满足不相关性，因此Λ满足RIP特性，可以重构得到原图像的恢复值。在重构端由S'恢复到S时，则左乘矩阵B此时有

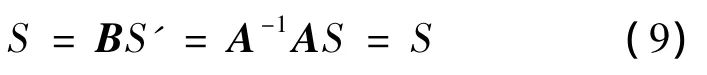
即由B和S'可以无损地恢复S。矩阵B:

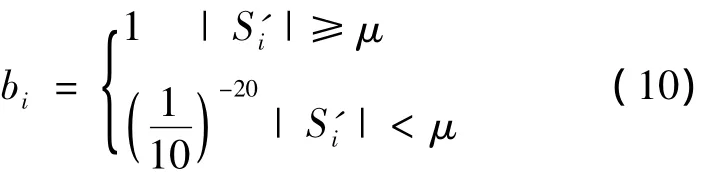
其中μ为S'第L个最大值。

利用OMP算法恢复S'，最后将4个高低频系数利用小波反变换恢复原图像。

门限矩阵对OMP算法改进后的算法流程如下:

输入:传感矩阵Λ =ΘA－1，观测向量Y=ΛS'，稀疏度为K;

输出:目标信号S'的K稀疏逼近;

初始化:残差r0=Y，索引集Γ0=∅，t=1;

循环步骤1)～5):

5)判断是否满足t＞K，若满足，则停止迭代;若不满足，则执行步骤1)。

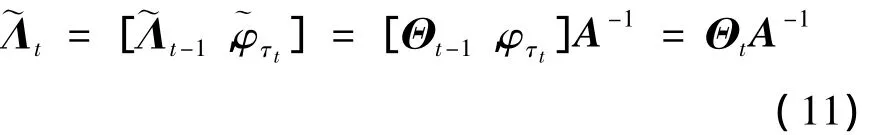
由式(11)及上述流程可知:

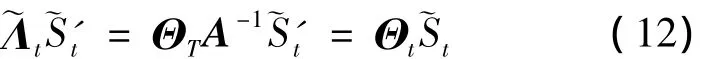
从而有rt=由上述流程可以看出，门限矩阵加入前后目标信号的稀疏逼近并没有发生改变，又由于S'比S稀疏度更好，从而稀疏逼近与S'之间的误差比与S之间的误差小，所以重构算法的精度得到了一定的改进。

具体算法步骤如下:

1)对原始图像进行DWT，获得高低频4个小波子带系数成分。

2)用加权矩阵A分别对LH1，HL1，HH1进行处理，得到3个子带的稀疏系数矩阵。

3)选择合适的M值，构造服从高斯分布的测量矩阵Ψ，分别对3个新的稀疏系数矩阵进行测量，得到3个子带的测量稀疏值矩阵，低频LL1子带系数保持不变。

5)将3个重构高频稀疏矩阵与LL1一起进行小波反变换得到恢复的图像。

3 实验及结果分析

实验基于PC机平台(CPU主频2.5 GHz，内存2 GB)，并用Matlab7.0实现程序仿真。为了取得良好的实验结果，分别选择了256×256 lena和256×256 Cameraman作为实验图像，选取近似对称小波Sym8对图像进行单层分解，测量矩阵为服从(0，1/N)的随机高斯矩阵，利用OMP算法进行恢复。根据单层小波分解高频系数的特点，每个分量稀疏分解后的系数大系数L即为加权系数矩阵的阈值，则单层高频水平分量的加权系数矩阵的阈值系数为第3 200个绝对值最大值，高频垂直分量阈值系数为第800个绝对值最大值，高频对角分量阈值系数为第190个绝对值最大值，选取参数p=20。

由于单层分解后高频子带均为128×128，所以测量矩阵行数满足0＜M≤128，选取M=120进行文中算法和单层小波变换压缩感知算法对两幅图像进行重构，重构结果如图2，3所示。分别取M=40，50，…，120采用文中方法和仅仅采用单层小波变换的压缩感知方法进行仿真;选取M=100，110，…，250，采用传统的算法进行同样仿真。

图2 改进算法对比Lena图像Fig.2 Restoring algrithms contrast of lena image

图像恢复质量的评判标准为图像的峰值信噪比，信噪比越高，图像的恢复质量越好。实验结果如图4，5所示，其中横轴为经过测量后的系数点个数，纵轴为恢复图像的峰值信噪比(PSNR)，PSNR为多次测量取平均值。可以看出文中提出的改进算法比原有算法有较明显的提高。

4 结语

介绍了压缩感知算法的原理和数学模型，在已有的单层小波分解压缩感知算法的基础上运用加权矩阵对算法进行了改进，利用加权系数矩阵使信号的稀疏分解进一步加强，接近更加理想的绝对稀疏;重构时采用OMP算法，仿真效果验证了改进方法的有效性。

［1］Donoho D.Compressed sensing［J］.IEEE Transactions on Information Theory，2006，52(4):1289-1306.

［2］LI De-lai，ZHANG Qiong，SHEN Hai-hong，et al.The application of compressive sensing based on wavelet in the reconstruction of ultrasonic medical image［C］//Second International Conference on Mechanic Automation and Control Engineering.Jinan，China:MACE，2011:5350-5353.

［3］Candes E，Romberg J，TAO T.Robust uncertainty principles:exact signal reconstruction from highly incomplete frequency information［J］.IEEE Transactions on Information Theory，2006，52(4):489-509.

［4］Mallat S G，ZHANG Zhi-feng.Matching pursuits with time-frequency dictionaries［J］.IEEE Transactions on Signal Processing，1993，41(12):3397-3415.

［5］Troppp J A，Gilbert A C.Signal recovery from random measurements via orthogonal matching pursuit［J］.IEEE Transactions on Information Theory，2007，53(12):4655-4666.

［6］Donoho D，Tsaig Y，Drori I.Sparse solution of underdetermined linear equations by stagewise orthogonal matching pursuit［J］.IEEE Transactions on Information Theory，2012，58(2):1094-1121.

［7］Needell，Deanna，Vershynin，et al.Signal recovery from incomplete and inaccurate measurement via regularized orthogonal matching pursuit［J］.IEEE Journal on Selected Topics in Signal Processing，2010，4(2):310-316.

［8］Hen S S B，Donoho D L，Saunders M A.Atomic decomposition by basis pursuit［J］.Siam Journal on Scientific Computing，1998，20(1):33-61.

［9］Malioutov D M，Cetin M，Willsky A S.Homotopy continuation for sparse signal representation［C］//2005 IEEE International Conference on Acoustics，Speech，and Signal Processing.Philadelphia:ICASSP，2005:733-736.

［10］Nowak R D，Figueiredo M A T.Sparse reconstruction by separable approximation［J］.IEEE Transactions on Signal Processing，2009，57(7):2479-249.

［11］Harmany Z，Thompson D，Willett R，et al.Gradient projection for linearly constrained convex optimization in sparse signal recovery［C］//2010 17th IEEE International Conference on Image Processing 2010.Hong Kong:ICIP，2010:3361-3364.

［12］Elad M.Sparse，Redundant Representations:From Theory to Applications in Signal and Image Processing［M］.New York:Springer，2010.

［13］岑翼刚，陈晓方，岑丽辉，等.基于单层小波变换的压缩感知图像处理［J］.通信学报，2010，31(8A):52-55.CEN Yi-gang，CHEN Xiao-fang，CEN Li-hui，et al.Compressed sensing based on the single layer wavelet transform for image processing［J］.Journal on Communications，2010，31(8A):52-55.(in Chinese)

［14］赵玉娟，郑宝玉.压缩感知中稀疏分解和重构精度改进的一种方法［J］.信号处理，2012，28(5):631-636.ZHAO Yu-juan，ZHENG Bao-yu.An improved method for sparse decomposition and resconstruction in compressed sensing［J］.Singal Processing，2012，28(5):631-636.(in Chinese)