企业战略联盟中知识共享的博弈分析

赵 炎，郭霞婉

（上海大学 管理学院，上海 200444）

一、引言

在转型深化期，外部知识更趋于全球化和多样化，为了更好地生存和发展，企业比以往更注重彼此之间的合作，并从各种形式不同的外部合作中获益良多。战略联盟便是一种典型而重要的企业间合作形式，罗杰·奈格尔和简·霍普兰德把战略联盟定义为两个或以上有着共同战略利益和相应经营实力的企业，为达到共同使用资源、共同拥有市场等战略目标，通过各种契约、协议而结成的优势相长或优势互补、风险共担、生产要素水平双向或多向流动的一种较松散的合作模式。Lawson and Samson（2001）也把联盟看做是企业降低成本与风险，获取规模经济，缩短新产品开发周期的有效手段［1］。

随着企业对联盟的热衷升温，学者们也逐渐重视把企业联盟作为外部知识获取机制来研究，在过去的15年间，这些研究已然成为管理学实证研究的一个重要部分。学者们一致认为，企业可以通过联盟来改变自身的技术和知识积累［2］。Song，et al.（2008） 对联盟企业的竞合关系以及企业之间知识资源的共享进行了研究，证实了联盟成员对于知识共享所带来的超额收益的期待促成了他们的结盟［3］。

但是，由于知识具备价值性与独占性，很多企业在结盟或合作研发时倾向于保留知识而非共享知识，并且合作伙伴总是希望对方多共享知识［4］。尤其在那些由来自于不同产业或者规模、实力不同的非对称企业结成的联盟中，这些问题更加突出，非对称企业在联盟后共享知识时总是存在着各种冲突与矛盾。

针对这一问题，在前人研究的基础上，本文引入企业知识转化为商业价值的能力水平、企业知识存储量、私有知识和共享知识及其转化弹性系数等变量，构建联盟企业知识共享博弈模型，求出知识共享的均衡解，并对其进行分析。进一步，本文将联盟划分为对称企业联盟和非对称企业联盟，并分别对其进行博弈分析和数值算例分析。通过分析知识共享主体间博弈过程，本文意在为企业战略联盟知识共享策略提供依据。

二、文献综述

联盟中成员企业通过共享知识，将得到两种收益：协同增效价值与倍增效应价值。前者是指由于联盟各方知识的互补性，它们融合在一起后能够产生大于成员各自知识的简单加和的效果；后者也被称作杠杆效应，指成员企业获得共享知识之后，提高了自身竞争优势的效应［5］。故而，知识共享对于联盟尤为重要，合作企业知识共享的研究也引起了诸多学者的关注。

目前，关于知识共享博弈的研究主要集中在三个领域［6］：①共享知识的影响因素研究，如成本、信任等，如赵慧娟［7］认为知识共享成本、失去的知识垄断利益以及共享得益等是影响知识共享的重要因素。②知识共享机制的研究，如Yung-Ming Li，et al（2010）［8］通过对COPs（Communities of Practice）的知识共享博弈模型分析，认为在成员的类型（成员所拥有知识的数量与质量）可观察而且由领导者负责整个组织的知识共享收益时，知识共享的收益将会达到最大化；张静（2007）［9］采用改进后的公平偏好博弈分析模型，构建了一个知识共享效用函数，以分析机制公平对知识转移的影响；还有研究证实在一些知识共享组织中，如果监视可以更好地发挥作用，那么组织成员间的知识共享行为将会得到有力的激励（King and Marks，2008）［10］。③知识共享过程激励方面的博弈分析研究，如张洪潮、何任（2010）等［11］通过对非对称企业合作创新的有限理性的进化博弈分析，得出惩罚机制和利益分配系数是决定企业联盟能否稳定合作不背叛的关键所在；Yung-Ming Li，et al（2010）［8］也提出可以通过引入奖励因素或建立知识管理系统、提升IT基础设施水平来提升知识共享收益。

而关于联盟的知识共享博弈分析研究也是层出不穷：Han T.J.Smit，et al（2006）以一种实物期权的评价方法建立了企业战略联盟价值的博弈模型，并以电子和电信业为例说明了企业在何种情况下建立战略联盟是最优选择，何时又应该独立运作［12］；王雪原、蔡野等（2010）从成员成本确定、成员收益确定、成员理性决策3个环节来设计基于显性资源和隐性资源的成员-联盟博弈模型，并给出创造成员-联盟期望交集的具体方法，来支持R&D 联盟决策者科学制定联盟发展战略［13］；宁烨等（2006）［14］指出在知识共享的过程中知识联盟的参与各方均要寻求知识共享成本与知识共享收益的平衡点，并采用完全信息动态博弈方法，分析了知识联盟在知识共享过程中的收益与成本等。

在现有战略联盟企业博弈分析的文献中，学者们分析了联盟成立的动机，联盟知识共享水平的高低博弈［4］，联盟企业选择知识共享与不共享的博弈［15］，联盟企业是否共享知识与是否监视的博弈模型［13］，联盟企业合作与背叛的博弈分析［11］以及知识共享激励模型［8］等等，但是这些文献对联盟企业知识共享的程度划分都是离散的，如高中低水平或者简单的共享或不共享等，并没有将将企业知识共享量作为连续变量进行研究；其次，学者们在分析联盟企业知识共享的过程时，没有考虑到企业自身将知识转化为商业价值的能力对企业知识共享决策的影响；再者，企业加入联盟以后，其知识可以分为私有知识和共享知识，而以往的文献中很少有考虑到私有知识对企业效用函数的影响。所以本文采用连续变量来衡量企业知识共享量，将企业的知识总量划分为私有知识和共享知识，并将它们与企业将知识转化为商业价值的能力一齐加入效用函数，建立n 个联盟企业知识共享的博弈模型。另外，由于非对称企业联盟的普遍存在，所以本文在第四部分中分析了非对称企业结盟后，其原有知识存储差距将将会对知识共享产生的影响，以期能对企业选择联盟伙伴时，提供参考价值。

三、联盟企业知识共享的博弈模型

（一）前提与假定条件

为考察两个或多个联盟企业知识共享过程及收益情况，我们假设：

（2）假设每个企业关于联盟项目的知识存量为Hi，自身保留不共享用来自己获益的知识量为hi。 那么，Hi=si+hi。

（3）假定企业的个人效用函数取柯布-道格拉斯函数形式，效用函数为

（二）模型建立

1.分散决策情况下的纳什均衡

在第二部分中的假设条件下，联盟中企业所面临的问题即为给定其他成员企业的知识共享水平的情况下，选择自己的最优策略（si，hi）来满足自己的效用Ei最大化。即

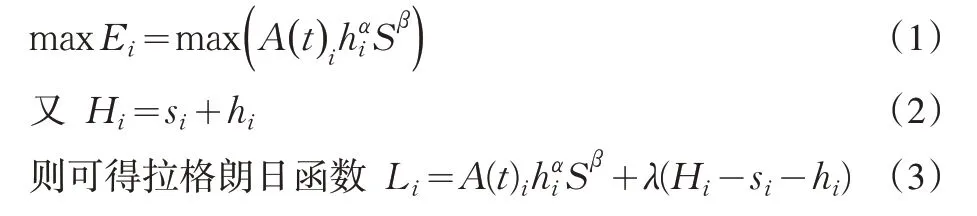
这里λ 是拉格朗日系数。

（3）式最优解的一阶条件为:

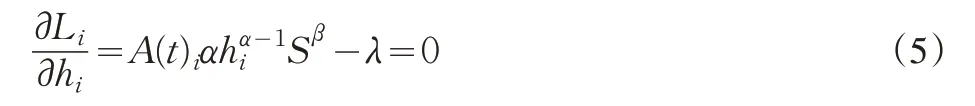
（4）、（5）经过化简之后，可得均衡条件

假定其他成员企业的选择已定，那么这n 个均衡条件决定了联盟内各成员企业知识共享的纳什均衡：

考虑到（2）式中的企业知识存量约束，整理可得企业贡献知识的反应函数为：

由于反应函数（8）中并无A(t)i，那么我们可以推断出联盟中成员的知识共享量与其知识转化为商业价值的能力是无关的。给定其他企业的选择，对于该企业来说，其知识共享的多少主要有以下几方面的预期来决定：①知识储存量，②私有知识转化为商业价值的弹性系数α，③联盟共享知识转化为商业价值的弹性系数β，④对其他企业贡献知识量。具体来说，本身知识存储量Hi越大，该企业倾向于共享更多的知识；β 相对于α 越大，说明联盟共享知识可以更好的给企业带来商业价值，所以，β 越大，企业共享知识的激励也越大；α 越大，说明企业保持私有知识对自己更有利，则该企业就偏向于不和联盟内其他企业共享知识；而且，如果企业相信其联盟合作伙伴共享的知识量越多，那么该企业自己的共享知识量就越少。

2.集中决策情况下的纳什均衡

上面模型是各成员企业自主决定是否共享知识来满足自己效用最大化的模型，这也这是现实中的情况。但是，根据Yung-Ming Li，et al（2010）［8］在其研究中指出的，在实践社区（Communities of Practice）知识共享的过程中，若有一位领导者可以统筹全局，也就是知识共享决策权高度集中于该领导者而非成员个体，知识共享水平要远远好于分散决策的情况。

在联盟中，若存在这样的领导者，那么该领导者制定决策就要满足联盟整体效用最大化的目标，即

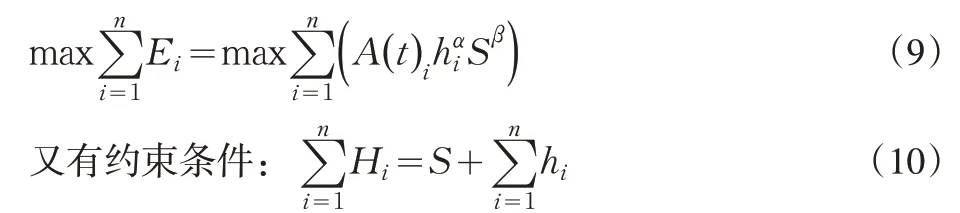
所以可得拉格朗日函数：

这里λ 是拉格朗日系数。

（11）式最优解的一阶条件为:

使用（13）中n个等式消除掉（12）式中的A(t)i，可得均衡条件：

给定其他企业的选择，此时，

将（15）式与（6）式进行对比，我们可发现在企业在分散决策时相对于集中决策倾向于多保留私有知识，这也是和Yung-Ming Li，et al（2010）的研究相吻合的。即若联盟中各企业知识共享决策由一个领导制定，那么联盟知识共享水平可大为提高，在这里，甚至可以达到帕累托最优。此时，企业的反应函数为：

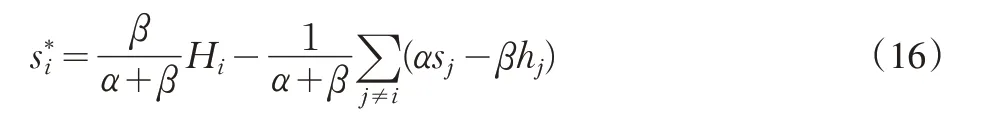
对比（16）与（8），就可以发现集中决策下的知识共享水平要高于分散决策。同样的，集中决策下的知识共享水平也不受A(t)i的影响。而且，在集中决策的情况下，共享知识转化为商业价值的弹性系数β 对知识共享水平的影响将变得更大，也说明领导者会更倾向于从联盟利益考虑问题。

四、模型推广与应用

（一）对称企业联盟的知识共享模型

对称企业广义上是指相同产业或规模、实力相当的两家或多家具有合作关系企业。在本文中将对称企业抽象为知识储备大致相当的联盟成员企业，即令

在均衡状态下，联盟内的每个成员企业将共享同等数量的知识，将（17）代入（8）式中，可得到每个企业的知识共享量：

那么，纳什均衡的总供给量为：

（二）非对称企业知识共享模型

当前中国处于转型深化期，企业越来越多的与规模、实力迥异，甚至跨行业的国内外企业结成非对称企业联盟以提高自身竞争力［11］。但是，非对称企业联盟面临着一系列问题，使这些企业间的合作创新关系难以持久，知识共享的不平衡便是其中的问题之一。针对这种情况，我们假定联盟中有两家企业，结合公式（2）、（8），可得二者的反应函数曲线，两曲线的交点便是知识共享的纳什均衡点。

1.企业知识存储量差距对知识共享的影响

假设联盟中两家企业的知识存储量的总和为3H，联盟共享知识转化为商业价值的弹性β=0.8，由于联盟存在的原因正是在于其可以通过知识分享与整合从而使成员优势互补，风险共担，降低成本，获取规模经济，缩短新产品开发周期（Lawson and Samson，2001）［1］，所以企业私有知识转化为商业价值的弹性α 应小于β，在本文中，取α=0.4 。结合（2）、（8）两公式，可得出不同企业知识存储实力差距情况下联盟知识共享量的变化曲线。

随着企业A原有知识存储量的变化，纳什均衡点的变化如图1 所示。图1 中横轴为企业A 所拥有的知识量x（0H ≤x ≤3H），纵轴为企业A或B的知识共享量，S1、S2分别表示企业A与企业B的知识共享量变化曲线。画一条垂直于x轴的纵线，该纵线与曲线S1、S2相交的点，便是企业A知识存储量为x 时，两企业达到纳什均衡时所选择的最优知识共享量。从图1 中可以看到，在企业A 的知识存储量较低（H1＜0.7H）时，它将不分享自己的知识，联盟共享知识主要由企业B（H2＞2.3H）提供，而且企业B 的知识共享量随着的企业B的知识存储量H2增大而增大。所以说，当企业原有知识存储量差距较大时，联盟知识共享博弈就类似一个智猪博弈，实力强大的企业是大猪，总是提供联盟共享知识；而实力弱小的企业就是小猪，总能从大猪提供的联盟共享知识中获益。

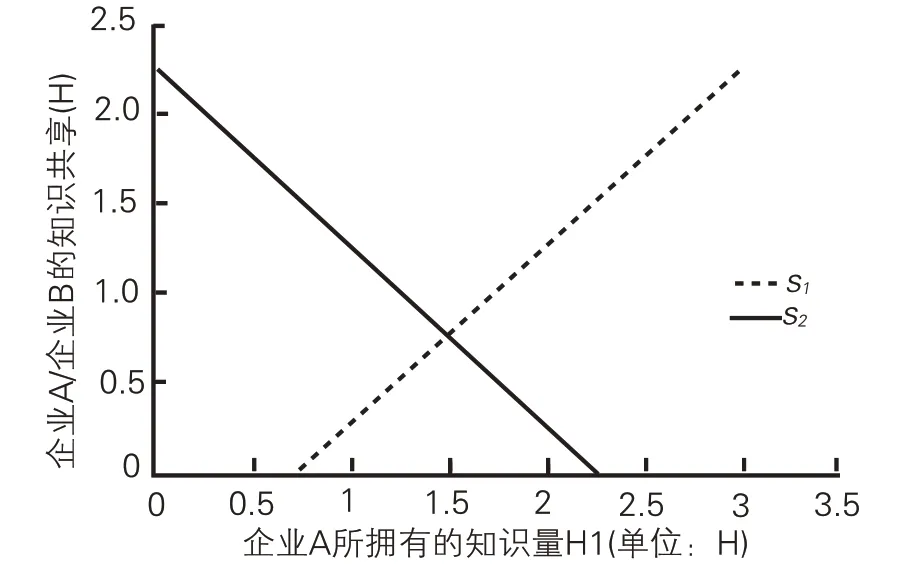
图1 联盟知识共享量随成员知识存储量变化趋势图

从图2 中可得，企业A 和企业B 知识总量固定为3H，随着企业A的知识存储量从0增长到3H，联盟的知识共享总量是先减少后增加的；当企业A的知识存储量位于0.8H到2.2H之间时，联盟知识共享总量S 稳定在1.5H。有趣的是，随着企业知识存储差距的拉大，虽然其中一个企业选择不共享知识，但是由于另一个企业共享了更多的知识，联盟总的知识共享量反而增大，最高可达到2.25H。

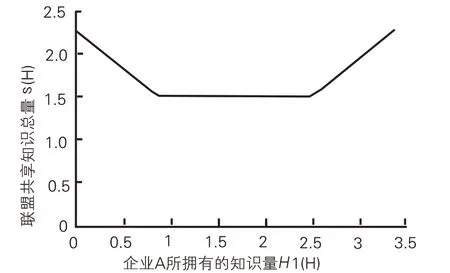
图2 联盟知识共享总量随成员知识存储量比例变化趋势图

2.企业自身知识储存量固定情况下选择联盟伙伴

针对自身知识存储量确定的企业A 如何选择合作伙伴，从而使自身在纳什均衡的状态下得到的最大化效益更大，我们假设企业A 的知识存储量为H，企业B 的知识存储量在0～10H 变化，仍然令α=0.4，β=0.8。结合在本文第三部分中得到的均衡解，可得到随着企业B知识存储量变化，企业A、企业B的知识共享量曲线（S1，S2）以及联盟知识共享总量（S）、企业A的效益曲线（E1）如图3和图4所示。

图3 企业A知识存储量固定情况下选择联盟伙伴企业B

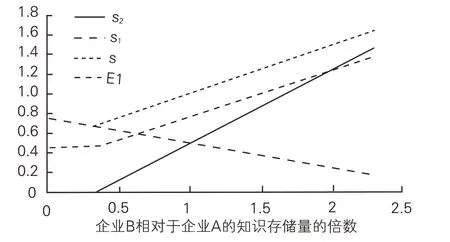
图4 企业A知识存储量固定情况下选择联盟伙伴企业B（局部放大图）

从图3 中可以看出，随着企业B 的知识存储量的增大，企业A 的知识共享量逐渐减少至0，企业B 则逐渐承担起共享联盟知识的主要任务。总体来看，企业A所获得的联盟效益也是呈上升趋势。将图3内企业B的知识存量在0～2H的部分放大，如图4 所示。我们发现在企业B 的知识储存量小于企业A的约0.3倍时，联盟知识共享总量反而随企业B的知识存储量增加而略微呈下降趋势。

五、结论与讨论

本文运用博弈论理论分析了联盟企业间知识共享行为，并且将联盟企业分为对称与不对称两种联盟模式进行深入分析。研究表明：

首先，传统意义上，我们往往认为，技术水平较弱，也就是将知识转化为商业价值的能力越低的企业，可能更乐意与合作伙伴共享知识。但是从本文的模型及推算中可以看出，企业知识共享的水平是和技术水平无关的，换句话说，不管企业将知识转化为商业价值的能力是强是弱，其知识共享水平只受联盟成员个数、自身知识存储量、私有知识转化为商业价值的弹性以及共享知识转化为商业价值的弹性的影响。

其次，若有领导者可以统筹全局，全权负责联盟企业知识共享项目，以联盟知识收益最大化为目标，来决策是否共享知识以及共享多少知识，那么联盟知识共享水平将大幅提高。但在当前的商业环境下，这样做会损害各成员企业的隐私与自主权，所以很难得到顺利实施。那么，联盟可以采取一些其他措施，比如推广知识管理系统以及完善IT基础设施等，以使联盟成员充分了解知识共享的过程与结果，并且可以通过加强沟通和制定协议等来提升知识共享收益［8］。

再次，两个非对称企业构建联盟，如果二者的原有知识存储量差距过大，则联盟知识共享博弈很可能会转化为智猪博弈，知识存储较多的企业会承担起主要的知识共享任务，而知识存储实力较弱的企业将会选择少共享甚至不共享知识。

最后，当联盟中两个企业知识存储实力差距不大时，总的联盟知识共享量反而比企业知识存储实力差距较大时要少。现实生活中，某些技术先进的企业会选择与一些未掌握核心技术的企业组成联盟，共享非核心知识并共同研发制造也是出于这个原因。在此过程中，技术占优的公司往往承担起产品的主要研发，而技术占劣的企业往往承担起非主要零部件研发以及产品加工制造，二者优势互补，从而创造出更多价值。

［1］Lawson B，Samson D.Developing innovation capability in or⁃ganisations：A dynamic capabilities approach［J］.Internation⁃al Journal of Innovation Managemen，2001，5（3）：377-400.

［2］Joanne Oxley，Tetsuo Wada.Alliance Structure and the Scope of Knowledge Transfer：Evidence from U S-Japan Agree⁃ments［J］.Management Science，2009，55（4）：635-649.

［3］Xiaozhong Song，Jinling Li，Nan Xu.Dynamic game analysis on knowledge-sharing and knowledge-spillover in competi⁃tive alliances［J］.Proceedings of the 2008 International Con⁃ference on Computer Science and Software Engineering，2008，12（15）：783-786.

［4］纪慧生.企业合作研发过程的知识共享博弈分析［J］.哈尔滨工业大学学报（社会科学版），2010，12（1）：91-94.

［5］陆瑾.基于演化博弈论的知识联盟动态复杂性分析［J］.财经科学，2006（3）：54-61.

［6］古继宝，张英，管凯.知识密集型企业项目组间知识转移博弈分析［J］.科学学研究，2006，24（S2）：590-594.

［7］赵慧娟.组织间知识共享的博弈分析［J］.商业时代，2008（13）：58-59.

［8］Yung-Ming Li，Jhih-Hua Jhang-Li.Knowledge sharing in com⁃munities of practice：A game theoretic analysis［J］.European Journal of Operational Research，2010，207（2）：1052-1064.

［9］张静.基于公平偏好的知识共享博弈研究［J］.科技与管理，2007，9（6）：17.

［10］William R King，Peter V Marks.Motivating knowledge shar⁃ing through a knowledge management system［J］.OMEGA，2008，36（1）：131-146.

［11］张洪潮，何任.非对称企业合作创新的进化博弈模型［J］.中国管理科学，2010，18（6）：163-170.

［12］Han T J Smit，Lenos Trigeorgis.Real options and games：Competition，alliances and other applications of valuation and strategy［J］.Review of Financial Economics，2006（15）：95-112.

［13］王雪原，蔡野.R&D联盟-成员博弈模型设计［J］.科技进步与对策，2010，27（12）：1-5.

［14］宁烨，樊治平，冯博.知识联盟中知识共享的博弈分析［J］.东北大学学报（自然科版），2006，27（9）：1046-1049.

［15］阮国祥，阮平南，宋静.创新网络成员知识共享演化博弈仿真分析［J］.情报杂志，2011，30（2）：100-104.