一种模块化多电平换流器数学模型的建立方法

李云丰，宋平岗，王立娜，卢 杰

（华东交通大学电气与电子工程学院，江西南昌330013）

目前为止，基于两电平电压源型的高压直流输电（high voltage direct current，HVDC）在国外得到了很好的应用[1-5]。模块化多电平换流器（modular multilevel converter，MMC）是新一代的高压直流输电的拓扑结构，由德国慕尼黑联邦国防军大学的R Marquart和A Lesnicar[6-7]在2002年首次提出的。西门子成为世界上第一个成功应用这个拓扑结构的公司，并将其命名为HVDC Plus[8]。我国将该技术统一命名为“柔性直流输电”，对应英文为HVDC Flexible，上海南汇风电场的MMC-HVDC示范性工程正是采用这种拓扑结构[9-10]。

传统基于电网换流方式的高压直流输电（LCC-HVDC）有难以克服的弱点，比如受端必需是有源网络、不能实现有功功率和无功功率的独立控制，因此需要补偿大量无功、谐波含量高，需要体积庞大的滤波装置等[11-12]。基于电压源（voltage source converter，VSC）两电平或三电平的HVDC，存在着大量器件的串联，器件的动态均压和静态均压问题成为制约这种技术应用的瓶颈，与LCC-HVDC一样，它同样需要体积庞大的滤波装置，增大了换流站的占地面积[1-2，13]。然而，基于MMC-HVDC将会很好的解决传统LCC-HVDC和两电平VSC-HVDC自身存在的弱点，因此受到了国内外学术界普遍关注[2，14-15]。本文在文献[3]的基础上，根据阶梯波调制，合理地假设当模块数量足够多时投入的模块为连续变化量，建立了相应数学模型，推导出了电容电压，桥臂电流，相间环流的时域解析表达式。

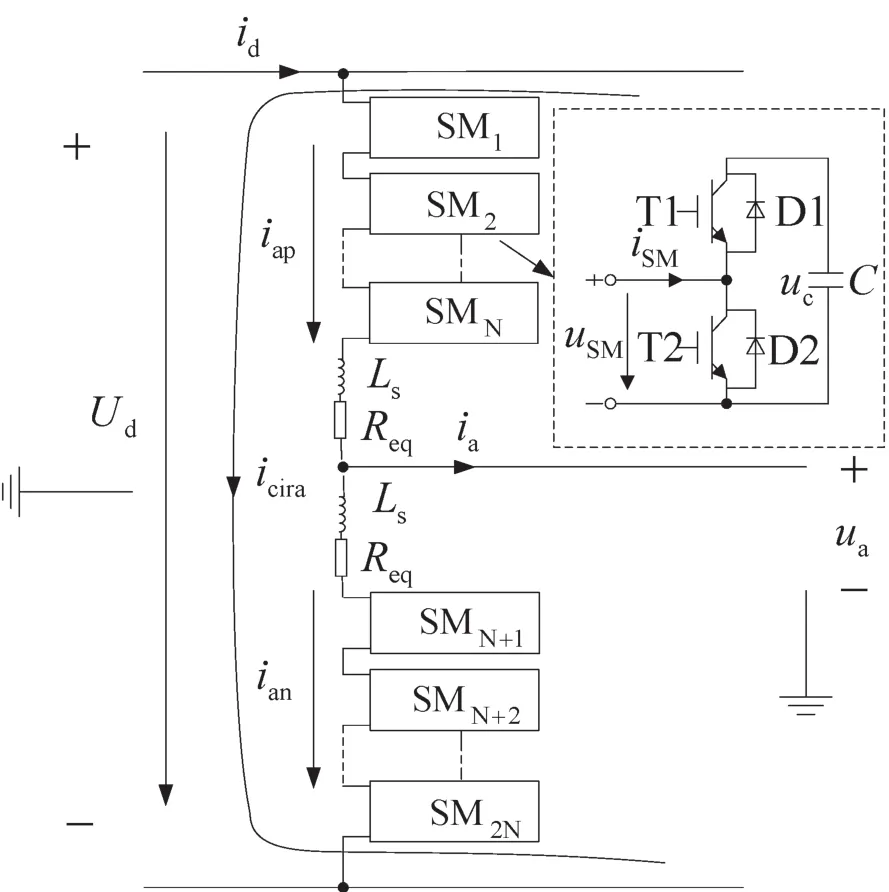
图1 MMC的基本拓扑结构Fig.1 Basic topology of MMC

1 MMC运行的基本原理

图1为MMC的基本结构图（只画出一相），每相由上桥臂和下桥臂构成，每个桥臂由一系列子模块（sub-module，SM）和限流电感Ls串联而成，Req为桥臂损耗等效电阻。SMi(i=1，2，…，2N)为子模块；ud为直流侧电压；id为直流侧电流瞬时值；iSM为子模块输出电流；iap，ian分别是a相上下桥电流，icira为a相环流；uSM为子模块输出电压；D1，D2为功率二极管；T1，T2为功率开关管；C为模块电容；uc为子模块电容电压。图1右上图是每个子模块的基本结构，分析子模块的工作特性可以知道，当上功率管T1开通，下功率管T2关断时，子模块投入工作；当上功率管T1关断，下功率管T2开通时，子模块被切除。

2 MMC的数学模型

根据MMC运行时的基本原理，得到子模块投入与切除的开关函数，Sji为开关变量函数

式中：i=1，2，…，2N，j=a，b，c，N为每相投入模块总数。分析MMC得到基本电压方程

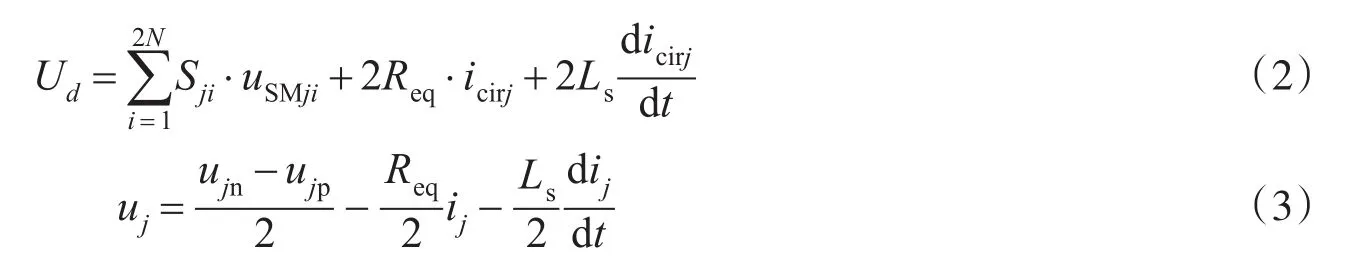
式（2）和式（3）中∶ud为直流侧电压；uSMji为 j相第i个模块的电容电压；ujp，ujn分别是上下桥臂投入电压大小；ucirj为产生相间环流的电感电压；uj和ij为 j相输出电压和电流；Req为子模块平均导通电阻和线路寄生电阻的等效值。考虑理想情况下，电容电压没有波动，相间环流可以忽略，得到MMC运行时的电流方程以及直流电压、输出电压和桥臂电压之间的关系

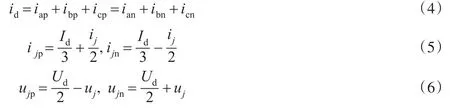
式（4）～（6）中，id，Id分别是直流侧电流的瞬时值和平均值，ijp和ijn分别是 j相上桥臂和下桥臂电流。为分析方便，以A相为例，设电压电流相角为ϕ，在图1中，令A相电压电流表达式为

3.1 MMC能量分析

MMC正常运行时，不考虑线路和换流站损耗时，一个周期内输送的有功能量全部消耗在受端，无功功率的交换则是由换流站和受端共同完成。正是因为能量的交换，导致模块电容电压的波动，结合MMC运行原理，上桥臂和下桥臂瞬时功率为

将式（5～7）代入式（8）中，并将式（8）中的两个方程相加减，可以得到

分析式（9）可知：

一个周期内当直流侧输出送的有功功率大于受端消耗的有功功率时，多余的能量将被模块内的电容吸收，模块电容电压平均值升高；反之，桥臂释放能量，缺少的能量由电容放电补偿，电容电压平均值下降；稳态时，电容电压平均值不变。

一个周期内三相桥臂之间不消耗有功功率，相间桥臂有功功率和无功功率的波动以2倍频并且为负序在三个桥臂之间传递。

上下桥臂之间能量的差值以工频频率在两个桥臂之间进行交换。

3.2 MMC解析表达式的推导与分析

MMC由一系列结构相同的子模块级联而成，每个子模块理论上对MMC运行的贡献率是一样，同样它们投入与切除的概率也是一样的。假设换流站在启动前各电容电压被预充电至同样的值，将上下桥臂各自看成是一个整体，开关频率一定高时[3]，子模块之间电压差值比较小，桥臂能量平均分配在各个子模块中，得到上下桥臂各自的能量方程

式中∶Δuap_sum(t)，Δuan_sum(t)分别是上下桥臂的波动电压总和。将式（8）代入式（10），再将式（10）两式相加减，只考虑波动的交流分量，得到Δuap_sum(t)，Δuan_sum(t)时域解析表达式

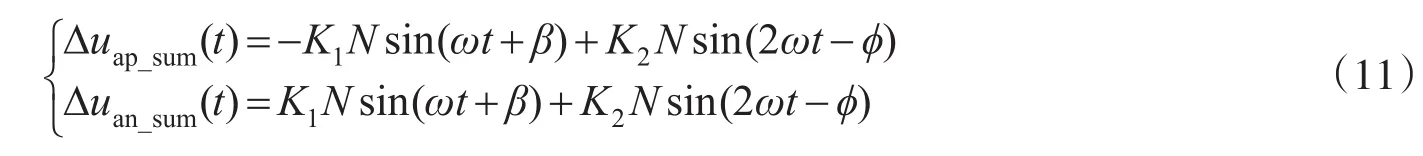
式中：K1=Scosϕ6ωCud；K2=S/12ωCud；k=3Ia/2Id；m 为电压调制度，m=2ua/ud；S=3uaIa/2；β=arctan[(k·sinφ/(k·cosφ-m))]。可以得到上下桥臂子模块电容电压的表达式

式中：Uc0为电容电压理想平均值。分析此式，可以得到以下结论：

电容电压中含有直流分量、工频频率波动分量、二倍频波动分量；

上下桥臂中电容电压的基波分量大小相等，相位相差180°，二倍频分量大小相等并且相位相同，桥臂电流中必含有二倍频的电流分量。

MMC主要应用于高压大功率场合，当子模块的数量足够多时，假设投入上下桥臂的子模块数目是成正弦规律变化的连续曲线，采用最近电平逼近方式进行调制完全可以满足上述假设，上下桥臂需要投入的模块数分别为

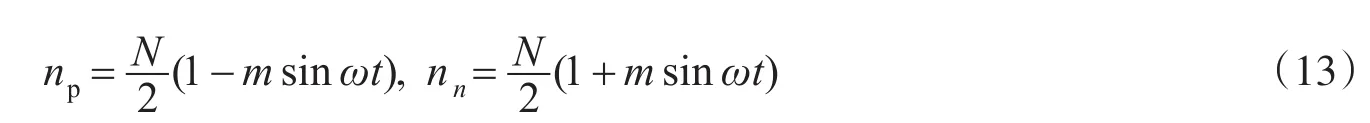
将式（12）与式（13）分别相乘得到上下桥臂投入工作的电压表达式为

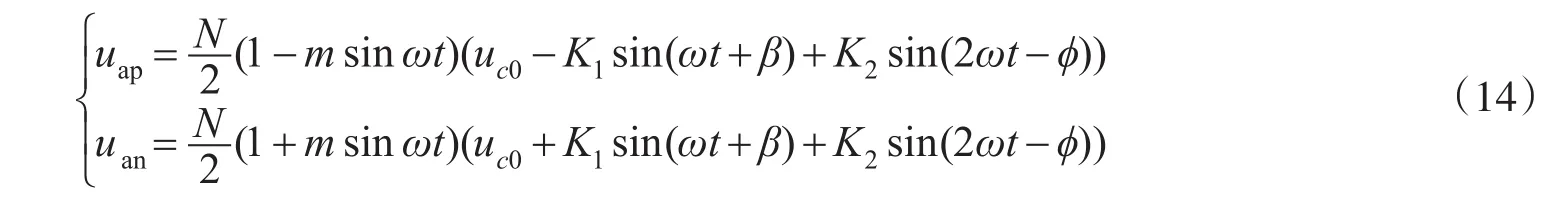
将式（14）两式相加，只考虑交流分量并根据式（2）可以得到电感两端电压以及环流表达式

式中：A=NmK1/8ωLs，B=NK2/4ωLs。结合三相桥臂可知[3]：

1）相间环流为二倍频的负序分量，环流没有直流分量和基波分量；

2）环流产生的损耗与其幅值的平方成正比；

3）环流的大小与限流电感Ls成反比，增大Ls的值可以降低环流的幅值，但是MMC动态特性会变差。

4）在电容电压平衡性一样的情况下，环流的幅值与投入总模块数和负载大小成正比。

于是式（5）和式（12）可修正为

4 仿真验证

在MATLAB中搭建了基于80个子模块的MMC系统，直流电压Ud=40kV，负载等效电阻R=10 Ω，L=10mH，限流电感Ls=10mH，电容C=25mF。

图2是电容电压平均波动仿真值与计算值之间的比较波形，纵坐标为电容电压平均值。图2中显示了两个波形在相位上是相同的，最大值和最小值基本一致。图3和图4为上桥臂电流仿真值和计算值以及相间环流仿真值和计算值，桥臂电流计算值含有直流分量、基波分量和二倍频分量，环流计算值只有二倍频量；两者的仿真值中不仅有这些量，也有高次的谐波分量，它们对波形的影响很小。

在实际应用中，一般都会产用开关频率优化算法和环流抑制算法，此时桥臂电流和环流计算的表达式将不再适用，因环流被抑制很小后，桥臂电流的表达式可近似用式（5）计算出。

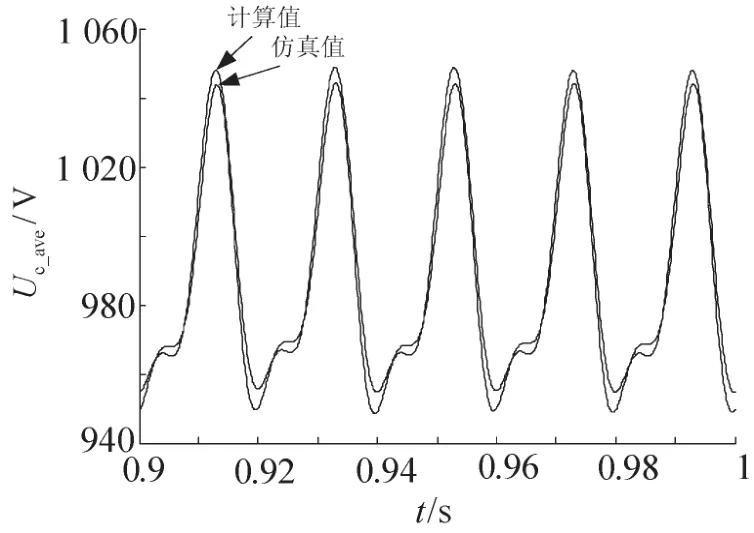
图2 电容电压平均波动仿真值与计算值Fig.2 Simulation and calculating results of capacitance voltage fluctuation on average

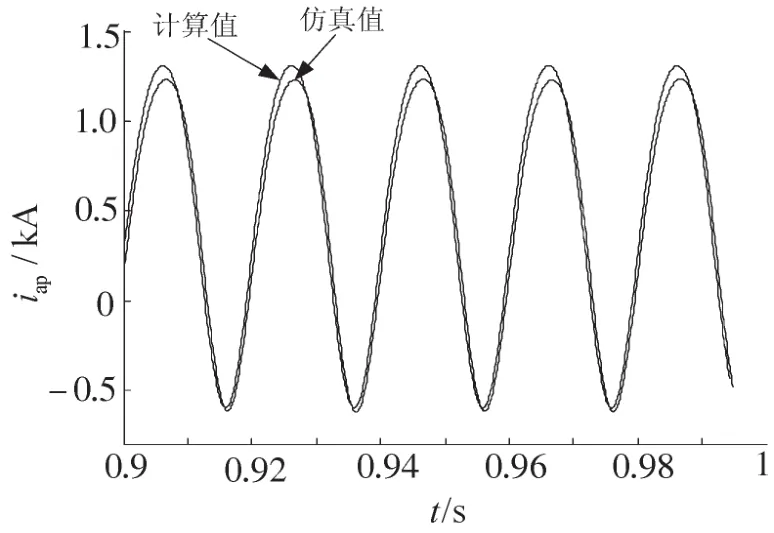
图3 桥臂电流仿真值和计算值Fig.3 Simulation and calculating results of arm current

图4 相间环流仿真值和计算值Fig.4 Simulation and calculating results of circulating current

5 结论

模块化多电平换流器是新一代的高压直流输电拓扑结构，本文在研究了MMC基本运行原理的基础上，对MMC进行了数学模型的建立，推导了模块电容电压、桥臂电流、相间环流的时域表达式。最后通过仿真模型，验证了所推导数学表达式是正确的。

[1]屠卿瑞，徐政，郑翔，等.模块化多电平换流器型直流输电内部环流机理分析[J].高电压技术，2010，36（2）：547-552.

[2]屠卿瑞，徐政，郑翔，等.一种优化的模块化多电平换流器电压均衡控制方法[J].电工技术学报，2011，26（5）：15-20.

[3]王姗姗，周孝信，汤广福，等.模块化多电平电压源换流器的数学模型[J].中国电机工程学报，2011，31（24）：1-8.

[4]SOLAS E，ABAD G，ABARREN A，et al.Modelling，simulation and control of modular multilevel converter[C]//14thInternational Power Electronics and Motion Control Conference，Ohrid Wikipedia：IEEE，2010：90-96.

[5]SOLAS E，ABAD G，ABARREN A，et al.Modulation of modular multilevel converter for HVDC application[C]//14thInternational Power Electronics and Motion Control Conference，Ohrid Wikipedia：IEEE，2010：84-89.

[6]LESNICAR A ，MARQUARDT R.An innovative modular multilevel converter topology suitable for a wide power range[C]//IEEE Power Tech Conference Proceedings，Bologna Italy：IEEE，2003：6.

[7]STEFFEN R，STEFFEN B，MARC H，et al.Modeling，simulation and analysis of a modular multilevel converter for medium voltage applications[C]//14thInternational Power Electronics and Motion Control Conference，Ohrid Wikipedia：IEEE，2010：775-782.

[8]郭捷，江道灼，周月宾，等.交直流侧电流分别可控的模块化多电平换流器控制方法[J].电力系统自动化，2011，35（7）：43-47.

[9]徐政，屠卿瑞，裘鹏.从2010国际大电网会议看直流输电技术的发展方向[J].高电压技术，2010，361（2）：3070-3076.

[10]江政昕，李广凯，王鸿雁，等.模块化多电平换流器直流输电稳态仿真分析[J].电气技术，2011（8）：5-9.

[11]李响，王志新，刘文晋.海上风电柔性直流输电变流器的研究与开发[J].电力自动化设备，2009，29（2）：10-14，20.

[12]姚伟，程时杰，文劲宇.直流输电技术在海上风电场并网中的应用[J].中国电力，2007，40（10）：70-74.

[13]刘钟淇，宋强，刘文华.采用MMC变流器的VSC-HVDC系统故障态研究[J].电力电子技术，2010，44（9）：69-72.

[14]陈诚，王勋，程宏波.三相PWM整流系统的研究[J].华东交通大学学报，2012，29（6）：40-44.

[15]宋平岗，王锴，兰洁，等.直接功率控制在三相光伏并网系统中的研究[J].华东交通大学学报，2013，30（1）：10-14.