基于综合成本优化的公交多模式站点停靠方法

舒 蕾，陈 峻，王 昊

(东南大学 交通学院，江苏南京210096)

公交停站模式的合理选择能够在一定程度上提升公交运营质量。目前，我国城市公交多采用单一站站停模式，大站快车和区间车等能有效提高公交运输速度的模式选用并不普遍。

公交停站模式选择作为公交调度的重要部分，受到国内外学者的持续关注，并取得一系列的成果。P.G.Furth［1］提出区间车和常规车协同编制时刻表的方法，目标是在可能的最小车队规模和最小乘客等候时间之间寻求均衡。S.P.Dell，等［2］提出在弹性需求条件下公交车辆运行优化模型。张健，等［3］考虑乘客和公交公司利益进行区间车优化，但忽略站点停车时间中乘客下车情况。傅昌建，等［4］提出大站快车可以满足不同乘客乘车出行需求。

对于快速公交，孙传姣［5］建立乘客出行时间成本和公交车辆出行时间成本最低的参数优化模型，考虑了全程车、区间车和大站快车3种不同车辆调度形式的组合。

针对轨道交通，R.V.Vukan［6］研究停站方案，提出各种停站方案组合的模型。郭钰［7］以停站与否为自变量，构建不同停站方案的基本优化模型。

选用多模式组合停站，一方面乘客出行过程中在站时间受到影响;另一方面车辆停站次数也随之改变，综合成本较单一站站停模式必然有所不同。同时，目前公交停站优化多默认公交站通行能力能够满足需求，但实际中通行能力多不能满足，造成公交车辆在车站延误，笔者把公交通行能力作为约束和检验进行公交多模式停站优化，以期达到综合成本最低。

1 公交停站模式描述

公交停站模式主要有站站停、大站快车和区间车3种，如图1。其中，站站停模式提供正常的公交上下客服务。大站快车和区间车为长距离出行和重点区域内的乘客出行服务，公交停站次数减少，运营速度提高，车辆周转时间缩短［8］。

图1 公交停站模式Fig.1 Mode of bus stop

目前常规公交多采用站站停模式，在少数线路辅助区间车模式，多模式停站未成为常态。若将3种模式组合，对于乘客，不同出行目的的乘客得到分类服务，降低互相影响，减少出行中的停留时间，缩短总出行时间;对于运营企业，停站次数减少，加减速频率降低，有效减少尾气排放，达到较高的燃油使用效率，降低系统运营成本。

但是，从乘客个体角度而言，多模式停站可能导致乘客等车时间和换乘次数增加，部分乘客根据自己出行的目的地更灵活地选择大站快车或者区间车进行换乘。同时可能在乘客出行习惯改变方面有一定影响，笔者对于乘客可能因不熟悉停站设置而导致的延误不做讨论，而将综合成本作为研究重点。

2 公交多模式停站优化模型建立

公交多模式停站带来综合成本的改变，模型以乘客出行成本和车辆运营成本两者最低为目标，考虑公交停靠站通行能力和客流等约束，研究特定时间段内，公交多模式停站的最优组合和发车间隔。

2.1 模型假设

1)在研究时间段内，公交车均匀时间发车。

2)研究线路的公交车车型是统一的。

3)公交车辆在站点的加减速时间和开关门时间相对固定，可以通过调查获得数据。

4)该条公交线路独享一个停车位。

2.2 停站模式影响因素分析及定量化表达

公交停站模式影响因素多样，笔者重点考虑公交通行能力、客流等因素并给出定量化表示，即约束条件。

2.2.1 停站模式影响因素分析

在多模式停站优化时，主要考虑以下因素：

1)公交通行能力。公交通行能力是车辆通行能力和乘客通行能力的双重定义，与停站模式的选择息息相关。既要提高通行能力，又不能浪费通行能力。

2)客运交通需求。各个站点的乘客OD量，需求是停站模式选择的基础和依据。客运需求大，且分布特征明显，采用多模式停站才可保障企业的运营效益和乘客的出行。

3)车队规模。公交线路所使用的公交车辆数量，尤其是高峰小时采用多模式停站，车队规模小很难满足乘客需求，规模大将导致资源浪费。同时，车辆的型号及性能等都有一定影响。

4)公交公司的经济效益。减少公交公司的运营成本，将有效提高其经济效益。采用多模式停站将影响到企业的经济效益。

5)社会效益。城市公交作为公用事业的一部分，在平衡公交公司的经济效益时，更要求提供社会服务。进行运营模式选择时要充分考虑公交的社会效益，考虑乘客节约的时间效益、乘客的舒适性等。

2.2.2 符号定义

在给出约束条件之前，对使用到的符号加以定义：i为公交车辆标记，i=1，2，…，M。j，k 为公交车站标记，j=1，2，…，N;k=1，2，…，N。O为各种停站模式：O=1，站站停;O=2，区间车;O=3，大站快车模式。T为研究时间段，min。

2.2.3 约束条件

根据影响因素分析，考虑公交通行能力、客流、时间点、发车间隔及满载率5个方面的约束条件。

1)公交通行能力约束

采用公共交通通行能力和服务质量手册［9］中的方法进行计算。每小时公交停靠站的通行能力(Bs)为：

式中：Bs为停靠站公交通能力，辆/h;Bl为单个车位的公交车通行能力，辆/h;Ncl为有效车位数;3 600代表单位时间，即1 h;为绿信比(有效绿灯时间占总信号周期的比例);tc为清空时间，s;td为平均停靠时间，s;Z为满足期望进站失败率的标准正态变量;cv为停靠时间波动系数。

单条公交线路一般占用一个固定的停车位，取有效车位数Ncl=1进行计算，每小时公交车站的客运通行能力则可以通过式(2)计算：

式中：P为客运通行能力，人/h;Pmax为每车额定最大载客量，人/车;f为额定发车频率，车/h;PHF为高峰小时系数。

在研究时间段T内，每小时每个车站车辆运送的乘客数必须不大于公交车站供该条线路使用的停车位的客运通行能力：

2)客流约束

客流约束是一些与乘客相关的变量之间的转换关系。式(5)～式(7)描述车上人数 Li，j、上下车人数(Bi，j、Ai，j)以及运送乘客数 Wi，jk之间的转换关系。式(8)、式(9)描述运送乘客数与剩余乘客数Si，jk之间的转换关系。rj是j站的乘客达到率，人/min：

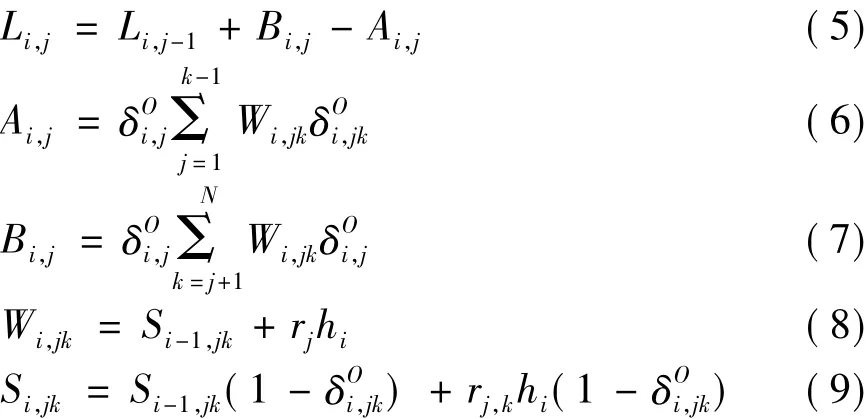
3)时间约束

式(10)、式(11)描述运行时间 ti，j到达时间 ai，j、停站时间T0和离开时间di，j的关系。式(12)～式(14)描述车头时距hi、车头间距hi，j以及研究时间段T之间的关系：

4)发车间隔约束

发车间隔需要在最小发车间隔和最大发车间隔之间。发车间隔小，通行能力小，发车间隔大，服务水平低。

5)满载率约束

约束条件含义是为保证乘客安全和舒适，车辆乘客满载率≤1。Pmax为每车额定最大载客量，人/车。

2.3 目标函数建立

以综合成本最优为目标函数，如式(17)，f1为乘客出行成本，f2为公交公司运营成本：

决策变量为发车间隔hi和停站模式Yi，Yi=1站站停模式，Yi=2区间车模式，Yi=3大站快车模式。

2.3.1 乘客出行成本

乘客出行成本即乘客从出发地到目的地所用时间成本。所用时间如图2。笔者忽略汇集时间和分流时间，只考虑候车时间、停靠站时间和在车时间成本。

图2 乘客运行过程分析Fig.2 Analysis of passengers’trip

车辆需要经过的一些时间点用参数表示，如图5。乘客出行成本由乘客候车以及停站和在车成本两部分组成。

图3 车辆时间点说明Fig.3 Explanation of vehicles’timestamp

一般而言，站站停模式下，每站乘客的等待时间为发车间隔的一半［5］，为 rjhi，j·hi，j/2，即车站乘客到达率rj与站点车头时距hi，j的乘积获得乘客数，乘以平均等待时间即为乘客候车时间。乘客等待区间车或大站快车时，可能遇到跳站情况，等待时间将增加。具体计算公式为 Si－1，jhi，即是被上一辆车跳过的剩余乘客数目 Si－1，j乘以车辆的发车间隔 hi。

乘客停靠站时间和在车时间成本和是否停站有关。第1部分是乘客在站间运行时间，假设车辆的标准运行速度不变，考虑干扰系数θi。第2部分为不下车的乘客车站停靠时间成本，由车辆加减速时间·c ，和停靠时间·T0两部分组成：

式中：Li，j·(t+c)为乘客等待进站开门时间成本;(Li，j－ Ai，j+Bi，j)·(t+c)为乘客等待出站关门时间成本; ( Li，j－ Ai，j)·max( Ai，j，Bi，j)u·(t+c)为车上乘客等待时间成本;c为平均每辆车的加减速时间，s;u为单个乘客平均上下车时间，s;t为车辆开关门时间，s;C1为乘客单位等待时间成本，元/min;C2为乘客单位在车时间成本，元/min。

2.3.2 公交公司运营成本

公司运营成本如式(19)。

式中：C3为乘客单位运营成本，元/min。

笔者重点考虑车辆的运营时间成本，包含车辆区间运营时间θiti，j，车辆在车站停车的车站加减速时间·c 和停靠时间·T0等 3 部分。

其中，T0包含车辆开关门时间和乘客上下车时间两部分，为：

2.4 参数关系说明

根据约束条件中各参数间转换关系绘制主要参数关系(图4)，从图4中可以看出，由到达率rj、未上车剩余乘客数Si，jk和决策变量hi可以推出运送乘客数Wi，jk，根据上下车乘客数可以得到在车乘客数Li，j。在时间相关参数上，根据发车间隔、到达时间和离开时间可以得到每站的车头间距。

图4 参数关系说明Fig.4 Parameter relationship

3 公交多模式停站优化算法设计

文中所建模型涉及站站停、大站快车和区间车3种不同的停站模式，复杂度为3O，O是发车的数量，与研究时间段和发车间隔有关。

模型为一个复杂的、典型的数学规划模型，采用传统的数学求解方法可以得到最优解，但计算量大，很多时候是难以实现的。遗传算法因其自身特性在解决此类问题时具有很强的优势，将决策变量用编码表示，更为合理和便捷［10］。

3.1 编 码

文中模型以发车间隔和运营模式为决策变量，只考虑分时段等间隔发车，公交的发车时序为一个数值串。采用可变长度的遗传算法编码，停站模式组合总的长度为发车次数，时间段确定根据发车次数即可得出发车间隔。

将各个出行选择停站模式的乘客做以下定义：X表示乘客数，上标代表运营模式，下标表示站点，N表示该站不停车，没有乘客在该站选择该种停站模式。详细见表1。

表1 乘客编码定义Table 1 Code definition of passengers

将乘客数量转化为二进制码，根据实际客流情况选择编码位数，以5位编码以及站点1进行说明。

当X=8时，编码中的一种情况是［00010，00010，00100］。

3.2 初始种群选取

采用完全随机的方法产生初始种群，即在优化过程中随机选取N个点作为初始解。

3.3 适应值计算

模型属于目标函数最小值模型，可以采用简单的适应值设置方法，如式(22)。为保证满足约束条件，在适应值函数上加入惩罚函数：

式中：F(x)为适应度函数;f(x)为目标函数;M为足够大的常数值。

3.4 遗传操作产生后代

1)选择：采用较为容易实现的轮盘赌法，依据个体的适应值计算每个个体在子代中出现的概率，并且按照概率随机选择个体构成子代种群。

2)交叉：采用双亲遗传法，按照交叉概率从选出的某条染色体随机选择染色体上的一个断点，交换双亲上断点的右端，生成新的后代。示例如图5。

图5 交叉示例Fig.5 Example of cross

3)变异：通过赋予每一个基因相对较小的变异概率Pm完成。对于图5中的A，对其进行变异，如图5。变异同时还要保证在可行解范围内，图6就不在可行解范围内。

图6 变异示例Fig.6 Example of variation

4 实例分析

将模型运用于实际的线路中，可以对模型进行检验，同时对实际线路停站模式进行优化，笔者以北京公交运通105线路为例进行分析说明。

4.1 实例背景

运通105线路沟通南北，穿越中关村科技园区等大型电子卖场，途径北京交通大学、北京理工大学、人民大学、清华大学、北京大学和北京体育大学等高校，路过圆明园景点，线路里程15.495 km，途径25个站点。现行发车间隔是12 min，不区分平峰和高峰。

根据实地调查，该线路采用站站停模式，存在以下问题：

1)车辆运营速度较低，运行速度集中在10～20 km/h;有些站点之间的运行速度低于10 km/h;

2)高峰时各线路车头时距不稳定，分布范围在0～20 s之间;

3)停站时间长(图7)，延误比较严重，高峰延误率100%，平峰略好(表2)，无论是高峰还是平峰都存在20 s以上的延误;

4)关键站点通行能力不足，海淀黄庄北车站的公交车辆通行能力为98辆/h，人民大学站的公交车辆通行能力为74辆/h，则该路段公交通行能力为74辆/h。根据调查可知该路段使用公交专用道，实际最大公交车流量为238辆/h，则这段车道的负荷度为238/74=3.216。公交车辆通行能力远远不能满足需求，拥堵严重。

图7 关键站点停站时间Fig.7 Block diagrams of dwell time

表2 部分关键站点平峰延误统计表Table 2 Delay statistics of platy kurtosis

延误原因：①与前车距离过近，后车无法离开，被迫等待;②公交车二次停车或多次停车;③客流不连续，等人;④其他。

4.2 参数确定

4.2.1 通行能力参数确定

与关键站点通行能力相关的参数如表3。

表3 关键站点通行能力相关参数Table 3 Corresponding parameters of the traffic capacity of key bus stop

运通105线路采用车辆拥有座位数39个，额定最大载客量为60人，高峰小时系数取0.85。

4.2.2 其他参数确定

研究时间段T为晚高峰时段1 h;线路上车站总数N=25;乘客单位等待时间成本C1=0.4元/min;乘客单位在车时间成本C2=0.2元/min;乘客单位运营成本C3=1元/min［5］;车辆加减速时间 c=40 s;单个乘客平均上下车时间u=5 s;t忽略不计。

根据实测观测到各个站点乘客上下车人数如图8。根据实际测得的每个车站上下车人数，按比例分配，得到站点乘客到达率。

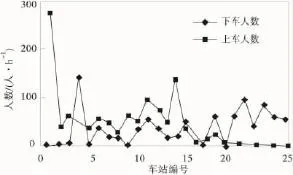
图8 各个站点乘客上下车人数Fig.8 Number of people getting on and off the bus

线路考虑干扰系数，根据实测情况得站点距离和运行时间如表4。

表4 线路基本情况Table 4 Route basic conditions

不同停站模式的车辆根据各站点客流情况确定的车站停靠方式如表5。

表5 不同车辆停站方式Table 5 Dwelling form of different schedule combination

4.2.3 计算参数确定

交叉概率 Pm=0.8;变异概率 Pc=0.005;种群大小取20;循环次数取100。

4.3 计算结果

计算得最终结果为发10次车，发车间隔为6 min，5辆采用站站停模式，1辆为区间车和4辆为大站快车。得到结果如表6，1代表站站停模式，2代表区间车模式，3代表大站快车模式。

表6 计算结果Table 6 Computation results

根据计算的结果，可以得到以下结论：

1)从表6的结果可以看出，优化之前每小时成本为23 352，优化后目标值为11 419，较优化前综合成本降低51.1%，优化效果明显。原因有两个：①公交发车时间缩短，乘客等待时间在减少且在目标函数中占主导作用，导致出行成本降低;②大站快车和区间车的比例逐渐增加，减少了主要站点乘客等待时间和总的出行时间，系统成本下降。

2)乘客等待时间减少，车站延误减少。将优化前在中关村南站停靠时间和优化后时间比较，可以发现：优化前运通105发车间隔为12 min，共5辆车，平均停站时间为38 s;优化后发车间隔为6 min，共10辆车，平均停站时间为21.1 s，在车站停靠时间减少。优化前停站时间不平稳，时间波动较大;优化后停站时间较为平稳，多在20～30 s之间。

3)误差分析。根据数据算得高峰小时发车间隔为6 min，1 h发10辆车，数据偏小，与该线路情况及实际调查客流数据相关。实际调查只做抽样调查，存在一定误差。在计算过程中，很多参数取平均值，也对结果产生一定影响。

5 结语

笔者以乘客出行成本和车辆运行成本最低为目标，综合公交通行能力、客流、时间和发车间隔等因素，分析停站模式的影响因素及定量化表示，建立停站模式组合优化模型并求解。实例表明，在客流特征明显时采用多模式停站，成本较单一模式停站有明显降低、停站时间显著减少、延误减少，具有一定的可行性和合理性。笔者将客流做定值考虑，在今后的研究中，如果能够结合动态公交客流预测结果，则可以实现公交停靠模式的实时优化。

［1］Furth P G.Short turning on transit routes［J］.Transportation Research Record，1987，1108：42-52.

［2］Dell S P，Filippi F.Service optimization for bus corridors with shortturn strategies and variable vehicle size［J］.Transportation Research：Part A，1998，32(1)：19-38.

［3］张健，李文权.城市公交区间车调度优化模型及算法研究［C］//2007年第三届中国智能交通年会论文集.南京：东南大学出版社，2007：90-96.Zhang Jian，Li Wenquan.Research on Optimal Model and Algorithm for Urban Inter-Zone Vehicle Dispatch［C］//3rdChina Annual Conference on ITS Proceedings.Nanjing：Southeast University Press，2007：90-96.

［4］傅昌建，杨彩霞，秦敏.关于公交车调度的优化问题［J］.工程数学学报，2002，19(2)：89-95.Fu Changjian，Yang Caixia，Qin Min.Optimization of dispatching buses［J］.Journal of Engineering Mathematics，2002，19(2)：89-95.

［5］孙传姣.快速公交调度优化研究［D］.西安：长安大学，2008.Sun Chuanjiao.Scheduling Combination of Bus Rapid Transit［D］.Xi’an：Chang’an University，2008.

［6］Vukan R V.Urban Transit：Operation，Planning and Economics［M］.New Jersey：John Wiley＆ Sons，Inc，2005.

［7］郭钰.城市轨道交通列车停站方案优化研究［D］.北京：北京交通大学，2009.Guo Yu.The Optimization of Stop Schedule Plan for Urban Rail Transit［D］.Beijing：Beijing Jiaotong University，2009.

［8］南振岐，滕彦芳，武尚磊.基于交通效率的城市公共交通路网研究［J］.兰州大学学报：自然科学版，2006，42(5)：76-78.Nan Zhenqi，Teng Yanfang，Wu Shanglei.Study on urban public traffic network based on traffic efficiency［J］.Journal of Lanzhou University：Natural Sciences，2006，42(5)：76-78.

［9］美国交通运输研究委员会.公共交通通行能力和服务质量手册［M］.杨晓光，腾靖，译.北京：中国建筑工业出版社，2010：15-16.TRB.Transit Capacity and Quality of Service Manual［M］.Yang Xiaoguang，Teng Jing，trans.Beijing：China Building Industry Press，2010：15-16.

［10］童刚.遗传算法在公交调度中的应用研究［J］.计算机工程，2005，31(13)：21-23.Tong Gang.Application study of genetic algorithm on bus scheduling［J］.Computer Engineering，2005，31(13)：21-23.