加铺层对旧水泥路面抗裂作用的理论分析
高嫄嫄,钟 阳,李 锐
(1.燕山大学 建筑工程与力学学院,河北 秦皇岛066004;2.大连理工大学建设工程学部,辽宁大连116024)
0 引言
水泥混凝土路面是一种常见的路面结构形式。随着经济发展需要,道路上行驶车辆不断增多,车辆超载现象时有发生,再加上气温、水分等自然因素的原因,道路经常出现早期损坏现象,其中路面中出现裂纹就是一种最常见的损坏形式[1],这直接影响了道路的使用性能并进一步加速了路面的破坏。所以对于含有裂纹路面的开裂机理分析及其加铺方法的研究成为工程界十分关注的热点问题[2-3]。
20世纪50年代,断裂力学作为一门学科建立起来,成为固体力学的分支,它是研究含裂纹构件强度和裂纹扩展规律的一门学科[4]。应力强度因子作为断裂力学中的主要参数,可以作为裂纹是否会继续扩展的一个主要指标。应用在工程结构的设计中[5]复变函数法[6-9]与积分变换法[10-14]是解决断裂问题及计算应力强度因子的主要方法,然而复变函数法多是分析无限大平面含有裂纹的问题且公式推导比较复杂,而积分变换法推导过程则相对简单。
笔者从位移控制方程出发,通过傅立叶积分变换并引入位错密度函数建立奇异积分方程,再应用Lobatto-Chebyshev法求解奇异积分方程,得到了裂纹尖端应力强度因子的解析表达式及数值解。最后以实际路面为例,对比了有无加铺层时水泥混凝土路面中裂纹尖端应力强度因子的变化情况,研究了加铺层的厚度及弹性模量对加铺效果的影响。
1 问题描述
水泥混凝土路面常用的计算方法是将其视为Winkler地基上的弹性板,而带裂纹并有加铺层的水泥混凝土路面的计算模型如图1。

图1 有加铺层含裂纹水泥混凝土路面模型Fig.1 Model of cement concrete pavement with crack
为了简化计算,将如图1的问题简化成3个子问题进行分析,如图2。子问题1〔图2(a)〕为不含裂纹且有边界偏荷载的有限宽度的平面问题;子问题2〔图2(b)〕为含有裂纹且在裂纹的表面作用对称荷载有限宽度的平面问题;子问题3〔图2(c)〕为含有裂纹且在裂纹的表面作用反对称荷载有限宽度的平面问题。由线弹性理论的叠加原理可知,3个子问题叠加的结果等价于图1模型中的问题。

图2 子问题Fig.2 Sub-problem
图2(a)模型的边界条件为:

图2(b)模型的边界条件为:

图2(c)模型的边界条件为:
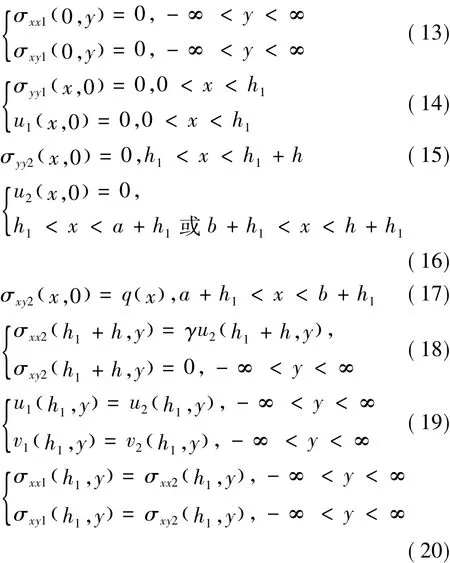
式中:σxxn和σyyn分别为第n层的沿x轴和y轴方向的正应力;σxyn为第n层的剪应力;un,vn为第n层沿x轴和y轴方向的位移 n=1,( 2),n=1 表示加铺层结构,n=2表示旧水泥路面结构;γ为地基模量。
2 p(x)和q(x)的求解
将子问题1中的坐标轴向右平移“l+L”个单位,偏荷载的问题转化为对称荷载的问题。对于子问题1中的应力与位移解析表达式的求解过程相对比较简单,所以这一部分不做详细论述。由线弹性叠加理论,子问题2、3中的p(x)和q(x)可表示成如下形式:

3 子问题2的理论分析
平面问题位移解法控制方程可统一表示为[15]:

对于平面应力问题k=(3-ν)/(1+ν),对于平面应变问题k=3-4ν,u为沿x轴方向的位移,v为沿y轴方向的位移,ν为泊松比。路面问题可以视为平面应变问题,所以取k=3-4ν。
由胡克定律,位移与应力之间的关系为:

式中:G为剪切模量。
考虑图1模型结构的对称性,为简化计算,由傅里叶变换理论[13],第 n层的位移 un,vn可以表示成如下的形式:

把式(25)、式(26)带入到控制方程式(22)、式(23)中,解微分方程组可以得到位移un,vn的表达式为:

式中:An1,An2,An3,An4是 η 的函数;Bn3,Bn4是 ξ的函数。
把式(27),式(28)带入式(24)中可以得到应力的表达式为:

由于计算模型中加铺层与旧水泥路面中ν的取值相差不大,并且为了推导公式的简便,这里取ν1=ν2= ν,即k1=k2=k。G1为加铺层的切模量;G2为旧沥青路面的剪切模量。
为推导方便,引入位错密度函数[11],定义为:

这样就可以用位错密度函数来表示未知函数An1,An2,An3,An4,Bn3,Bn4( n =1,2)。
由边界条件式(6)和式(7)及位错密度函数的定义式,并应用留数定理计算积分就可以得到[16]:

由边界条件式(5)、式(10)、式(12)并经傅里叶逆变换可以得到:


求解由式(33)~式(40)组成的线性方程组得到 A11,A12,A13,A14,A21,A22,A23,A24。
将 A21,A22,A23,A24,B23,B24带 入 边 界 条 件 式(9),经化简可以表示成如下的形式:

φ(x,t,η),p(x)可采用 Gauss-Laguerre 数值求积公式来计算其的数值解。
为方便计算,将积分限变换到(-1,1),式(41)可以表示为:

由于裂纹尖端具有 -1/2阶奇异性[5],所以对于平面内含有裂纹的情况,可设
用Lobatto-Chybshev求积公式来求解奇异积分方程,式(56)可以改写为:

由位错密度函数的性质,对于平面内部含有裂纹问题可以得到补充方程:

式中:ωj为权函数,
再由应力强度因子的定义[14]:

经整理可以得到:

4 子问题3的理论分析
由于子问题3的荷载具有反对称性,其应力位移可表示成如下形式:


为简化计算,引入位错密度函数:

子问题3的公式推导过程与子问题2类似,因此不再做详细的论述。子问题3的应力强度因子可表示成如下的形式:

5 计算实例
为分析影响含裂纹水泥混凝土路面加铺效果的主要因素,以实际水泥混凝土路面为例,应用文中的公式推导过程及Lobatto-Chybshev数值求解方法计算路面裂纹尖端应力强度因子的数值解。对比有无加铺层时应力强度因子的计算结果、分析加铺层厚度及弹性模量对应力强度因子计算结果的影响。
图1的水泥混凝土路面各参数的选取如下:P=700 000 N/m,L=0.15 m,G1=1.6 ×109N/m2,h1=0.1 m,G2=1.15 × 1010N/m2,γ =1.3 × 109N/m2,h2=0.25 m,k=1.6,裂纹的长度为 d=b - a。具体计算结果如图3~图5。

图3 有无裂纹时应力强度因子Fig.3 Comparison of stress intensity factors of the crack tips(b)with and without overlay

图4 不同加铺层厚度时应力强度因子(裂纹长度d=0.02 m)Fig.4 Stress intensity factor of the crack tips(b)with different thickness of overlay

图5 不同加铺层厚度时应力强度因子(裂纹长度d=0.02 m)Fig.5 Stress intensity factor of the crack tips(b)with different share modulus of overlay
从图3的计算结果中可以看到:无论是Ⅰ型裂纹还是Ⅱ型裂纹,加铺层的存在都使其应力强度因子值有所减小,特别是对于Ⅰ型裂纹,加铺层的作用更加明显。
从图4的计算结果中可以看到:随着加铺层厚度的增加,Ⅰ型裂纹的应力强度因子有所减小,但是减小的程度不是很明显。加铺层厚度的增加对Ⅱ型裂纹尖端应力强度因子值基本没有影响,所以对于旧水泥混凝土路面表面出现裂纹的状况,盲目的增加加铺层的厚度并不是明智的选择。
从图5的计算结果中可以看到:加铺层弹性模量的增加对Ⅰ型裂纹的应力强度因子的影响并不明显,对Ⅱ型裂纹应力强度因子也基本没有影响。所以,改变加铺层弹性模量并不是有效的阻止旧水泥混凝土路面表面裂纹扩展的有效的方法。
6 结论
笔者以断裂力学理论为基础分析加铺层对旧水泥混凝土路面的抗裂作用。从位移控制方程出发,采用积分变换并引入位错密度函数推导出在含有裂纹水泥混凝土路面在有加铺层的情况下应力强度因子的解析表达式,并通过数值计算对比了有无加铺层时裂纹尖端应力强度因子的变化情况,从中可以看出加铺层对于含有裂纹的水泥混凝土路起到了抗裂作用,同时,加铺层的厚度也是影响其抗裂性能一个主要因素。
[1]钟阳,程培风,苏跃宏,等.路基路面工程[M].北京:科学出版社,2005.Zhong Yang,Cheng Peifeng,Su Yuehong,et al.Subgrade and Pavement Engineering[M].Beijing:Science Press,2005.
[2]马银华,易志坚,杨庆国.结合式水泥砼路面加铺层的力学性能分析[J].重庆交通学院学报,2005,24(2):42-45.Ma Yinhua,Yi Zhijian,Yang Qingguo.Analysis about the mechanical properties of combined-form concrete pavement overlays [J].Journal of Chongqing Jiaotong University,2005,24(2):42-45.
[3]凌天清,赖辉,韦刚,等.刚性基层长寿命沥青路面抗反射裂缝力学分析[J].重庆交通大学学报:自然科学版,2010,29(5):714-717.Ling Tianqing,Lai Hui,Wei Gang,et al.Mechanic analysis on defending reflective crack of perpetual asphalt pavement with rigid base[J].Journal of Chongqing Jiaotong University:Natural Science,2010,29(5):714-717.
[4]丁遂栋.断裂力学[M].北京:机械工业出版社,1997.Ding Suidong.Fracture Mechanics[M].Beijing:China Machine Press,1997.
[5]张行.断裂力学中应力强度因子的解法[M].北京:国防工业出版社,1992.Zhang Xing.Solution of Stress Intensity Factor in Fracture Mechanics[M].Beijing:National Defense Industry Press,1992.
[6]库贵华,张少雄.断裂力学教程[M].西安:西北工业大学出版社,1994.Ku Guihua,Zhang Shaoxiong.Fracture Mechanics[M].Xi’an:Northwestern Polytechnical University Press,1994.
[7]Zak A R,Williams M L.Crack point stress singularities at a bi-material interface[J].Journal of Applied Mechanics,1963,30:142-143.
[8]Korniets S D,Kaminskii A A.Stress around a crack in an elastic plate weakened by two holes[J].International Applied Mechanics,1987,23(11):1072-1077.
[9]Vroonhoven J C W.Stress intensity factors for curvilinear cracks loaded under anti-plane strain(mode III)conditions[J].International Journal of Fracture,1993,70(1):1-18.
[10]李永东,贾斌,张男,等.功能梯度材料有限宽板的反平面断裂问题研究[J].应用数学和力学,2006,27(6):683-689.Li Yongdong,Jia Bin,Zhang Nan,et al.Anti-plane fracture analysis of a functionally gradient material infinite strip with finite width[J].Applied Mathematics and Mechanics,2006,27(6):683-689.
[11]Zhao Huaqing.Fracture and Fatigue Analysis of Functionally Graded and Homogeneous Materials Using Singular Integral Equation Approach[D].Baltimore:Johns Hopkins University,1998.
[12]Kadioˇglu S,Daˇg S,Yahsi S.Crack problem for a functionally graded layer on an elastic foundation[J].International Journal of Fracture,1998,94:63-77.
[13]Erdogan F,Gupta G.The stress analysis of multi-layered composites with a flaw [J].International Journal of Solids Structures,1971,7:39-61.
[14]Sei U,Tatsuya M.The surface crack problem for layered elastic medium with a functionally graded non-homogeneous interface[J].Journal of Solid Mechanics and Material Engineering,2002,45(3):371-378.
[15]李永东.断裂力学理论与应用[M].北京:科学出版社,2000.Li Yongdong.Theory and Application of Fracture Mechanics[M].Beijing:Science Press,2000.
[16]林益,刘国钧,叶提芳,等.复变函数与积分变换[M].武汉:华中科技大学出版社,2008.Lin Yi,Liu Guojun,Ye Tifang,et al.Complex Function and Integral Transform[M].Wuhan:Huazhong University of Science and Technology Press,2008.

