斜靠式拱桥振动特性分析

王建秋，何发礼，朱东生

(1.重庆交通大学土木建筑学院，重庆400074;2.成都城投基础设施建设投资有限公司，四川成都610015)

0 引言

斜靠式拱桥是近年来发展起来的一种新型拱桥结构形式。它由4片拱肋组成，中间2片主拱竖直或稍向外倾斜，主拱两侧各1片向内倾斜的斜靠拱肋，两两组合形成空间受力体系。中间平行拱肋为桥梁的主要承重结构，桥面开阔、畅通，每侧倾斜拱肋与相邻竖直拱肋构成人行桥的空间。外拱与内拱组成空间稳定体系，提供了结构的稳定性［1］。斜靠拱能改善平行拱的受力性能，增强横向稳定，有效解决施工中面外稳定问题，同时斜靠式拱桥极富美学价值，成为城市景观桥梁中极具竞争力的一种新桥型［2］。

斜靠式拱桥出现的时间较晚，国内外建成的数量也不多，故其研究成果相对较少。此类桥梁结构空间效应明显，受力行为复杂，有关学者进行了一些研究。陈淮，钟轶峰，等［3-5］以平顶山市城东河路湛河桥为例，得出斜靠式拱桥的自振特性及结构的低阶振型特征主要以拱肋的横向失稳为主;李莹［6］对影响斜靠式拱桥结构内力和稳定性的主要设计参数进行了研究，指出该结构横向刚度较弱;刘爱荣，等［7-8］探讨了副拱倾角变化对结构稳定性的影响，通过单向地震输入，得出随副拱倾角改变拱肋轴力、弯矩和位移的变化规律。笔者以拉萨市柳梧大桥为例，分析了在地震作用下柳梧大桥的动力特性，由于该桥的副拱倾角较大，其动力特性出现了一些新特点;在此基础上对其进行时程分析，探讨了地震波单向输入与三维输入时对结构内力的影响;通过三维地震波输入，探究副拱倾角改变对结构动力特性及地震响应的影响。

1 工程背景

拉萨市柳梧大桥(图1)主桥为斜靠式钢箱拱桥，主跨的上部结构由主拱和副拱构成，主拱计算跨径L=120 m，矢跨比f/l=1/4.615;副拱计算跨径L=130 m，矢跨比f/l=1/4.330。主、副拱轴线均为二次抛物线，其拱肋均为单箱单室橄榄型截面，拱肋截面宽度沿跨长相等，高度沿跨长自拱顶向拱脚(沿水平方向x)呈线性增加。主拱轴线平面为竖平面，副拱轴线平面与竖平面夹角为30°。桥跨结构为中承式，主、副拱间设16道横撑，将主副拱连结成空间体系。吊杆为Φ5和Φ7平行钢丝束，吊具为冷铸镦头锚。主拱吊杆为交叉对称布置(交叉角呈45°)，同一梁端的两吊杆具有不同的荷载特性(内力和线刚度);主拱吊杆的截面分别为 127Φ5，187Φ5，10Φ7和163Φ7等4种截面。副拱吊杆与人行道横梁外端相连，锚固于副拱肋上，平行布置，吊杆倾角互不相同，其最大外倾角为38°，同一梁端的两吊杆截面分别为61Φ5和55Φ7。

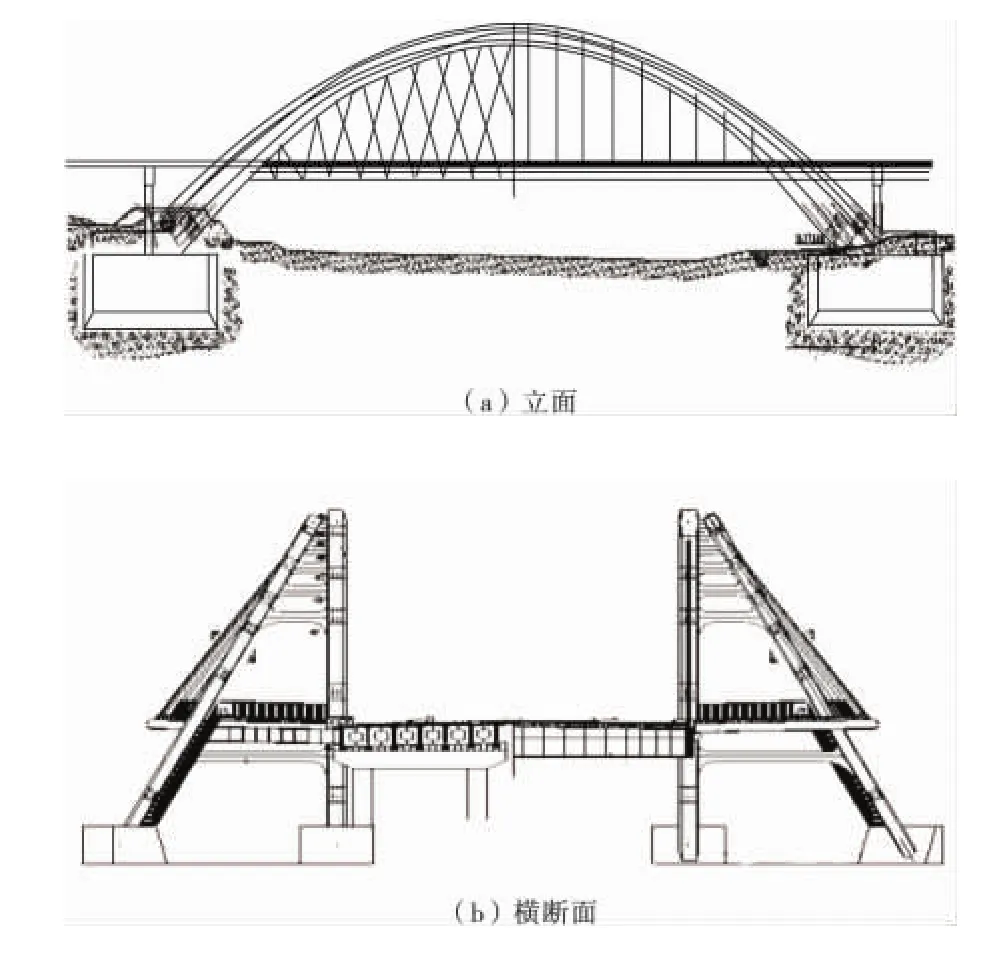
图1 柳梧大桥立面和横断面Fig.1 Elevation and cross section of Liu-Wu Bridge

拉萨市柳梧大桥桥道系包括车行道和人行道。车行道由钢横梁(主梁)、钢纵梁、纵置R.C连续桥道板组成。其中横梁为桥道系主要承重结构，通过吊杆支承于拱肋上，为向桥道系提供刚度而设置的纵梁及纵向联结系，均不直接承受荷载。由于拱跨结构受力的需要，人行道平面上呈弧线悬出。人行道由横梁、纵向联结系以及纵置R.C桥道板构成。横梁内端竖向支承于车道横梁端部的牛腿上，斜吊杆产生的水平力，则通过牛腿处人行道横梁与车行道横梁端部接触处之间的竖向弧形支座传递，因此人行道横梁和车道横梁间呈铰接联系，均为压弯杆件。横梁外端通过斜向吊杆支承于副拱肋上，纵置R.C桥道板简支在横梁上，桥面铺装连续。

2 动力特性

柳梧桥的分析采用MIDAS/Civil有限元分析软件，主拱、副拱及桥面系的端横梁、中横梁、人行道横梁、纵梁、主副拱间横撑均采用梁单元模拟，吊杆采用桁架单元模拟。全桥空间有限元计算模型见图2。

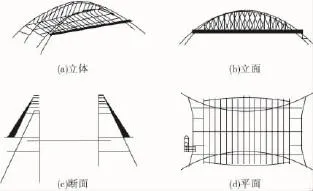
图2 全桥空间有限元计算模型Fig.2 The finite element calculation model of bridge

采用子空间迭代法进行计算，得到了该桥的动力特性。限于篇幅，笔者仅列出了该桥的前15阶振型的频率、周期及其振型特征，见表1。

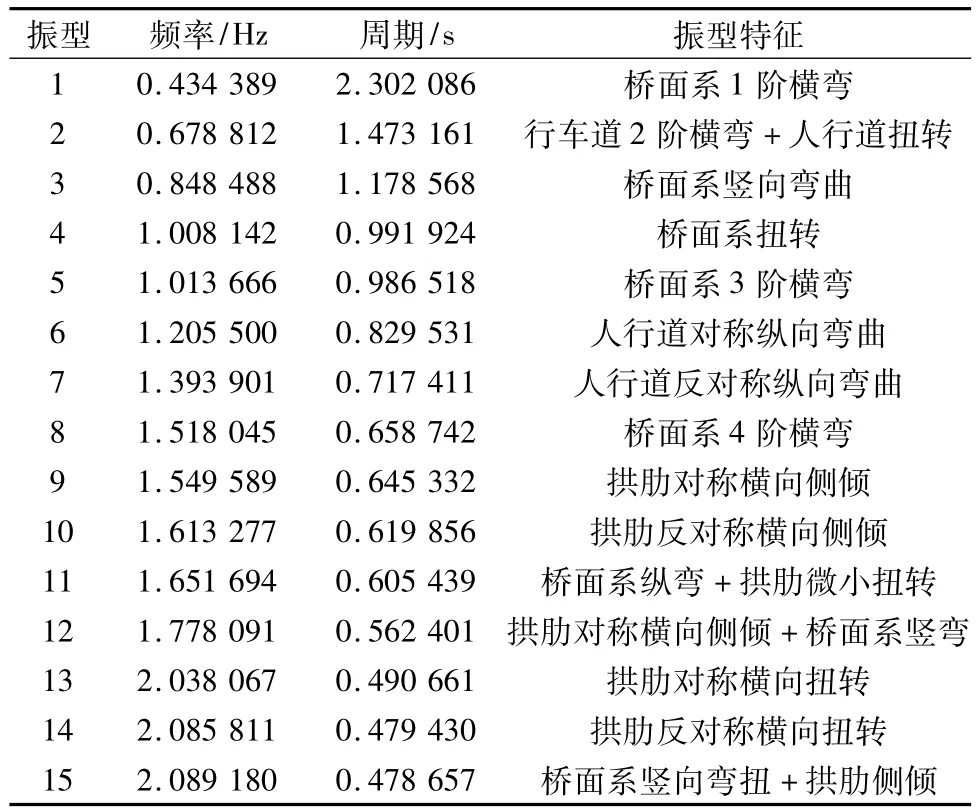
表1 全桥动力特性Table 1 Dynamic characteristics of bridge

斜靠式拱桥由于其结构形式及传力方式与一般拱桥相差较大，导致其动力特性也相应出现了一些新特点。柳梧桥全桥均为钢结构，由表1可以看出，该桥的振动形式较为复杂。其1阶振型为桥面系的横弯，其周期较长，说明桥面系刚度相对较弱，主要是车行道、人行道及横向联系的构造原因，其构造采用角钢或工字钢。另外，人行道横梁与车行道横梁的链接为铰接，这也使得在低阶振型中，多以车行道的横弯，人行道的扭转、纵弯为主。直到第9阶振型才出现拱肋侧倾，说明该桥拱肋的横向刚度相对较大，这与斜靠拱的倾角较大及拱肋截面构造有很大的关系。

3 地震响应分析

采用时程分析法对柳梧大桥进行地震响应分析。选取El Centro(180 Deg，峰值加速度为0.214 2 g)地震波，按照不同的输入方式，定义了4种工况。工况1:El Centro波纵桥向输入;工况2:El Centro波横桥向输入;工况3:El Centro波竖向输入;工况4:El Centro波三维输入。各个工况拱肋各控制截面内力值见表2～表5。

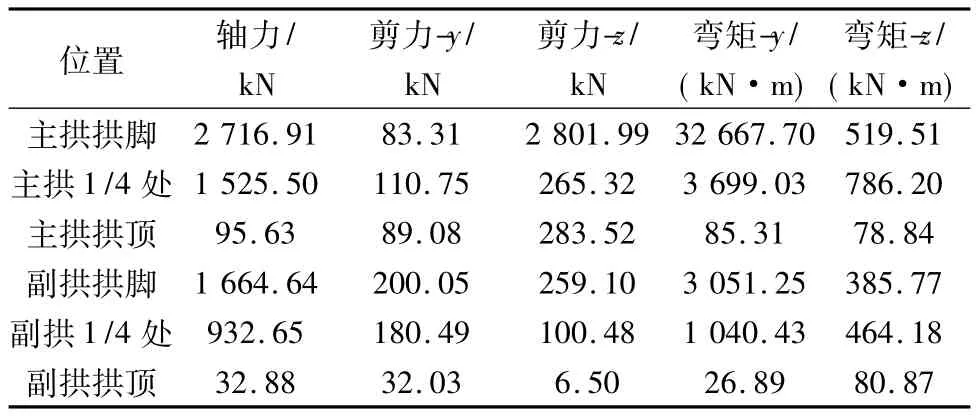
表2 El Centro波纵桥向输入各截面内力值Table 2 Internal forces of each section by inputting El Centro in longitude direction

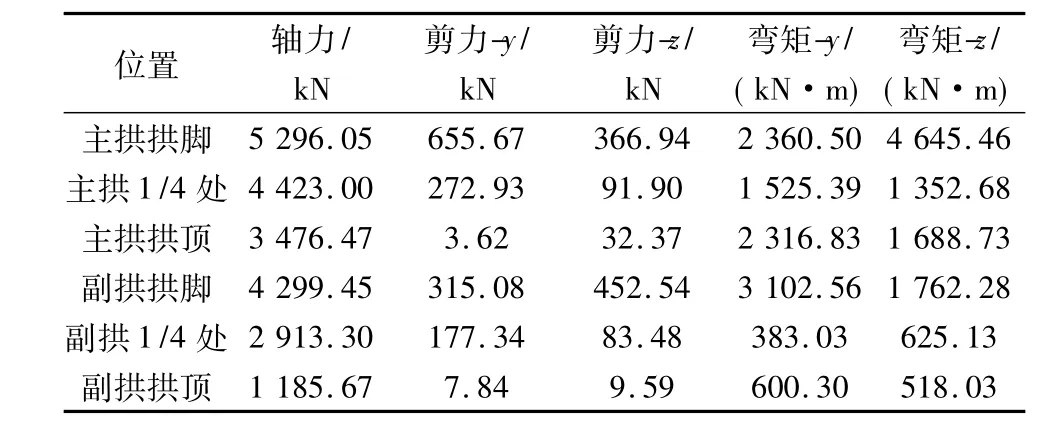
表3 El Centro波横桥向输入各截面内力值Table 3 Internal forces of each section by inputting El Centro in transverse direction

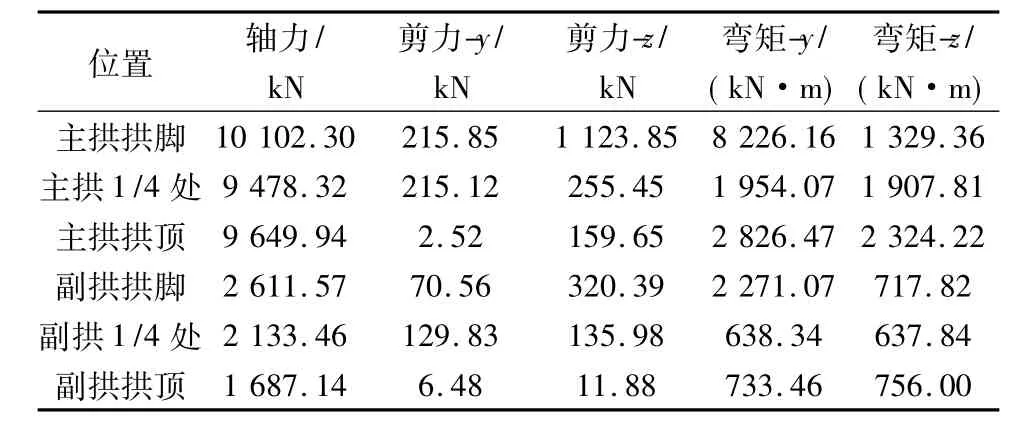
表4 El Centro波竖向输入各截面内力值Table 4 Internal forces of each section by inputting El Centro in vertical direction

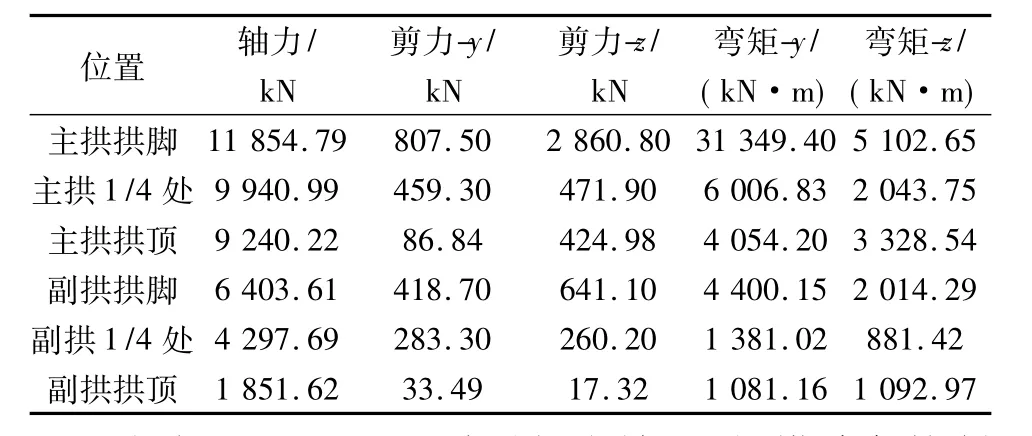
表5 El Centro波三维输入各截面内力值Table 5 Internal forces of each section by inputting El Centro in three direction

由表2可见，地震波纵桥向输入时，拱肋各控制截面轴力相对较小，主拱各截面轴力均比副拱略大，且沿着拱轴线方向由拱脚向拱顶各控制截面轴力减小趋势很明显，拱顶轴力很小;主拱拱脚的纵向剪力和面内弯矩比其他截面大很多，剪力和弯矩值也沿着拱轴线方向由拱脚向拱顶减小;说明当地震波纵桥向输入时，对结构影响最大的为主、副拱拱脚截面，而对拱顶截面的影响很小;同时纵桥向地震波对结构纵向剪力和面内弯矩的影响较大。

由表3可见，地震波横桥向输入时，各控制截面轴力较地震波纵桥向输入时均有增大，对副拱轴力的影响大于主拱，对拱顶截面轴力的影响大于其它截面;对主拱横桥向剪力和面外弯矩影响显著，尤其是拱脚截面，表明地震波横向输入时对结构作用主要表现在横向剪力和面外弯矩的变化上。

由表4可见，地震波竖向输入时，主拱各控制截面轴力较副拱大4～5倍;主、副拱各截面轴力之间变化较小;主拱肋各控制截面轴力要比纵桥向输入时大很多，拱脚截面增大近4倍，拱顶截面增大的更多;而拱脚的剪力和弯矩则小于纵桥向和横桥向地震波输入时的值;由此表明竖向地震波对结构的轴力大小起决定性的作用。

由表5可见，地震波三维输入时，各控制截面内力较单向输入时均出现了较大值，但并不是单向输入时各工况内力叠加之和，其最大值只比单向输入时的最大值略大;故在做某一方面的分析时，为了分析方便和计算简洁可以选择对其影响较大的单方向输入地震波即可。另外，主拱肋为结构主要的承重构件，无论单向还是三维输入地震波时，主拱肋各控制截面内力均较大，尤其是拱脚截面，故在此类结构设计中应重视主拱拱肋，对拱脚部位做加固处理。

4 副拱倾角变化对结构性能的影响

4.1 副拱倾角变化对动力特性的影响

由于柳梧大桥动力特性的特点，与之前该类桥梁的分析结果有些不同，如其低阶振型为拱肋的横桥向侧倾［5］;另外，该桥的副拱倾角为 30°，在同类桥梁中较大，为进一步探讨副拱倾角对斜靠式拱桥动力性能的影响，笔者分别取 10°，15°，20°，25°，30°，35°等6种副拱倾角进行分析，得到该桥的频率如表6。

由表6可以看出，该桥的自振频率随着副拱倾角的增大而增大，说明副拱倾角的增大可以显著改变斜靠式拱桥的整体刚度;副拱倾角变化对斜靠拱桥的低阶频率影响较大，第1阶频率的增幅为6%，而第15阶频率的变化很微小;当副拱倾角在20°～25°之间变化时，斜靠式拱桥的自振频率波动较小。

副拱倾角的变化对斜靠式拱桥低阶振型特征的影响较大。当副拱倾角小于20°时，其低阶振型以拱肋的侧倾为主;且随着角度的减小，拱肋的侧倾程度明显加大。当倾角大于20°时，其低阶振型则以桥面系的横向弯曲为主;且随着角度的增大，拱肋出现侧倾的阶次越来越大，副拱倾角为25°时，第7阶模态出现拱肋的侧倾，倾角为30°时，第9阶出现拱肋侧倾。说明副拱倾角的增大可有效的提高拱肋的横向刚度和面外稳定性。

表6 副拱各倾角对应的频率值Table 6 Frequency value corresponding to each angle of vice arch /Hz

4.2 副拱倾角变化对地震响应的影响

副拱倾角变化对斜靠式拱桥拱肋地震内力和位移响应的影响，刘爱荣，等［7］已经做了一定的研究，即分别考虑了横桥向与纵桥向单向地震输入时，拱肋内力和位移的变化。在实际情况中，地震发生时地震波的传播是多方向的，为更全面的考虑地震作用下结构的响应，笔者采用反应谱法同时考虑3个正交方向(水平方向x、y和竖向z)地震动作用，模态组合采用CQC(完全平方和)，得到主副各控制截面的轴力、弯矩及拱顶的横向位移随副拱倾角变化的情况，见图3～图5。

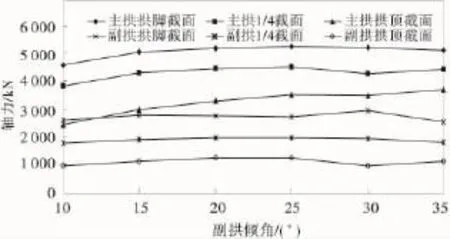
图3 拱肋轴力随副拱倾角变化Fig.3 Stress of arch rib changing with the vice arch angle

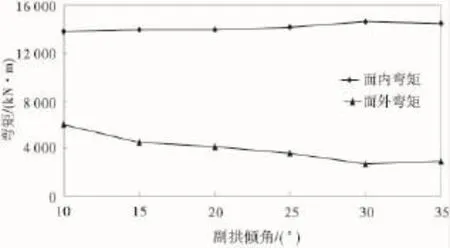
图4 主拱拱脚弯矩随副拱倾角变化Fig.4 Bending moment of arch feet changing with the vice arch angle

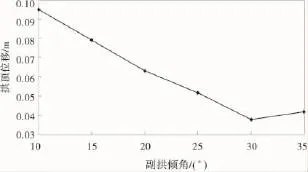
图5 拱顶横向位移随副拱倾角变化Fig.5 Lateral displacement of arch top changing with the vice arch angle

由图3可见，在同时考虑3个方向地震作用时，副拱倾角的增加对主拱轴力的影响较明显。副拱倾角由10°增加至20°时，主拱各截面轴力均有所增加，分别增加 11.4%，12.2% 和 25.6%;而角度由20°变化至35°主拱各截面轴力变化均较小;副拱各截面轴力变化很小，只有在副拱倾角为30°时，副拱拱脚截面轴力略有增大，拱顶轴力有所减小。这主要是因为随着副拱倾角的增加，副拱重力的竖向分力越来越大，使得在开始阶段主拱各截面轴力有所增加，而随着副拱倾角的增加拱肋刚度增大，增幅越来越小，刚度相对达到了一个稳定值，故结构响应也趋于稳定，轴力变化微小。

由图4可见，随着副拱倾角的增加，主拱拱脚的面内弯矩值变化较小;主拱拱脚的面外弯矩则随着主拱倾角的增加而减小，副拱倾角为10°时，面外弯矩值为6 024.81 kN·m，副拱倾角为 30°时，面外弯矩值为2 681.7 kN·m，面外弯矩减小55.5%。在副拱倾角为30°时达到最小值，副拱倾角增大到35°时面外弯矩值有所增加。这表明副拱倾角变化对主拱拱脚的面外弯矩的影响较大;副拱主要起到减小拱肋的面外弯矩增加结构横向稳定性的作用;而倾角的增大也要适当，倾角过大会对结构起反作用。

由图5可见，副拱倾角由10°增大至30°的过程中，图中直线斜率较大，表明副拱倾角在此范围内变化时，对拱顶横向位移影响较大;拱顶的横向位移随副拱倾角的增大而减小，副拱倾角为10°时，拱顶位移值为0.095 1 m，副拱倾角为30°时，拱顶位移值为0.033 7 m，位移减小60.4%。可见拱肋倾角的增大对该结构横向刚度的提高、拱顶横向位移的减小起到很重要的作用。副拱倾角在30°时，拱顶横向位移出现最小值，而在副拱倾角由30°增大至35°的过程中，拱顶横向位移有少量的增加。这也说明副拱倾角应该在合理的范围内增加，使其对结构产生的作用达到最佳。

5 结论

根据柳梧桥的结构特点，结合有限元计算分析得出以下结论:

1)该桥桥面系的横向刚度相对较小，低阶振型特征以桥面系的横弯和人行横道纵弯为主，主要是因为桥面系横、纵梁为型钢构成，人行道横梁与行车道横梁联结为铰接。

2)当地震波单向输入时，纵桥向地震波对结构纵向剪力和面内弯矩影响较大，横桥向地震波对结构横向剪力和面外弯矩影响较大，竖向地震波对拱肋轴力起决定性的作用;而地震波三维输入时，结构各截面内力均出现了较大值。

3)无论是单向还是三维输入地震波，主拱肋各控制截面内力均较大，尤其是拱脚截面。故在此类结构设计中应重视主拱拱肋，对拱脚部位做加固处理。

4)副拱倾角变化对斜靠式拱桥的频率和振型特征影响较大，对低阶频率的影响大于高阶频率;随着副拱倾角的增大，拱顶横向位移显著减小;即副拱倾角在合理的范围内适当增加，可提高结构的性能。

［1］肖汝诚，孙海涛，贾丽君，等.斜靠式拱桥［J］.上海公路，2004(4):22-26.

Xiao Rucheng，Sun Haitao，Jia Lijun，et al.Leaning-type arch bridges［J］.Shanghai Highways，2004(4):22-26.

［2］肖汝诚，孙海涛，贾丽君，等.昆山玉峰大桥——首座大跨度无推力斜靠式拱桥的设计研究［J］.土木工程学报，2005，38(1):78-83.

Xiao Rucheng，Sun Haitao，Jia Lijun，et al.Kunshan Yufeng bridge design of the first long span leaning-type arch bridge without thrust［J］.China Civil Engineering Journal，2005，38(1):78-83.

［3］陈淮，申哲会，胡锋，等.斜靠式拱桥动力特性研究［J］.郑州大学学报:工学版，2005，26(4):25-28.

Chen Huai，Shen Zhehui，Hu Feng，et al.Study on dynamic characteristics of leaning-type arch bridge［J］.Journal of Zhengzhou U-niversity:Engineering Science，2005，26(4):25-28.

［4］钟轶峰，殷学纲，陈淮.斜靠式异型拱桥体系振动特性分析［J］.桥梁建设，2005，2:8-11.

Zhong Yifeng，Yin Xuegang，Chen Huai.Analysis of vibration characteristics of leaning-type irregular-shape arch bridge system［J］.Bridge Construction，2005，2:8-11.

［5］陈淮，孙应桃.斜靠式拱桥拱肋倾角变化对稳定性能的影响［J］.铁道科学与工程学报，2009，6(1):21-24.

Chen Huai，Sun Yingtao.Variation sloping angle of arch rib influenced on the stability of double X-shaped arch bridge［J］.Journal of Railway Science and Engineering，2009，6(1):21-24.

［6］李莹.斜靠式梁拱组合体系桥梁设计理论研究［D］.上海:同济大学，2006.

Li Ying.Research on Design Theory of Leaning-Type Arch Bridge System［D］.Shanghai:Tongji University，2006.

［7］刘爱荣，禹奇才，张俊平，等.斜拱肋倾角变化对斜靠式拱桥地震响应的影响［J］.暨南大学学报:自然科学版，2010，31(3):270-273.

Liu Airong，Yu Qicai，Zhang Junping，et al.Influence of variation of incline angle of inclined arch rib on the seismic response of leaning-type arch bridge［J］.Journal of Jinan University:Nature Science，2010，31(3):270-273.

［8］刘爱荣，禹奇才，宋瑞，等.地震作用下斜靠式拱桥的动力稳定性［J］.深圳大学学报:理工版，2010，27(3):286-289.

Liu Airong，Yu Qicai，Song Rui，et al.Dynamic stability of leaning-type arch bridge under earthquake［J］.Journal of Shenzhen U-niversity:Science and Engineering，2010，27(3):286-289.