薄壁管件校直工艺中壁厚对截面扁化变形的影响
翟 华,李小慧,赵彩暇,陈善奇
(合肥工业大学 机械与汽车工程学院,安徽 合肥 230009)
0 绪论
薄壁管件是航空航天、船舶中广泛采用的零件,在校直与其他加工过程中容易发生截面变形,直接影响到薄壁管件的尺寸精度和表面质量。文献[1]提出了一种基于傅立叶三角关系来解决弯管弯曲问题的半解析方程,用简单经济的有限元方法来测定弯曲管道的应力场。文献[2]采用半解析公式测定曲管的弹性与最终限制因素。文献[3]从薄壁管件未知位移场的无限极傅里叶级数模式里,求解适合一般载荷和边界条件的精确解。但对于压力校直工艺中,壁厚对薄壁管件截面变形的影响并不多见。本文主要在现有的薄壁管件校直理论和实践基础上,采用理论分析、仿真分析和实验研究相结合的方法,分析薄壁管件壁厚对截面变形影响问题。
1 薄壁管件的截面变形
如图1所示,研究薄壁管件弯曲的某一小段。先假设管件的横截面积不产生翘曲,管件的中心线与弯曲中心轴重合,且材料是不可压缩的。令A0为管件中面上的点,沿周向的位移为v,径向的位移为w。A点到管件中面的距离为z,则A点沿周向的位移为vz,沿径向的位移为wz。假设A0A在变形前后都为直线,则可以推出A点的轴向应变εθ、周向应变εΦ与位移的关系。
根据文献[6],管件单位体积内的内力功为:
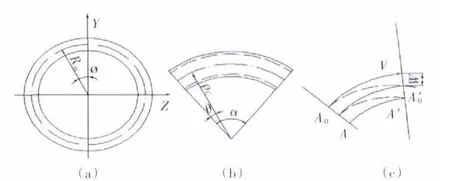
图1 管件的弯曲变形

积分之后,可以得到:
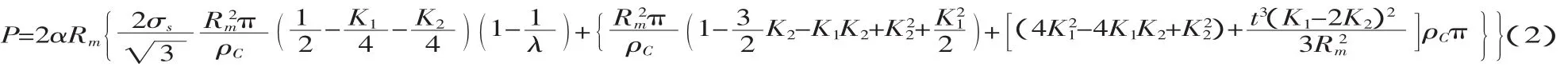
定义壁厚影响截面扁化指数为

2 薄壁管件的截面变形的校直仿真与实验
薄壁管件在校直过程中,不仅管件会产生轴向弯曲,也容易产生截面变形。薄壁管件截面扁化变形影响因素很多,本节通过仿真探讨壁厚对管件在校直过程中截面质量的影响。
仿真用试件为35钢,长L=500mm,半径r=36mm,杨氏模量 215GPa,泊松比 0.3,密度 ρ=7.85g/cm3,屈服强度315MPa。壁厚对锆合金管件校直的影响,利用ANSYS软件,分别对壁厚为2mm、3.5mm的薄壁管件进行仿真计算,分别在压头上通过对式(2)求解K1,K2,可以得到:

按式(4)画出如图2所示的壁厚对截面扁化的影响曲线图。

图2 壁厚对截面扁化影响
由图可以看出,对于具体的管件来说,其材料特性轴向是一致的,当轴向弯矩相同的时候,壁厚对于截面的变形有非常重要的影响。管件比较厚时,壁厚影响截面扁化指数较大,截面抵抗变形能力强,壁厚影响截面扁化指数小,截面抵抗变形能力低。
加载如表格1所示载荷,并记录薄壁管件受该载荷作用时1点、2点、3点的位移变化。如图3a、b是当载荷为600N时壁厚为2mm和3.5mm的管件Y方向变形,即轴向位移变化;图3c、d是当载荷为600N时壁厚为2mm和3.5mm的管件X方向位移变形,即管件截面扁化形变形。对壁厚分别为2mm和3.5mm的薄壁管件,分别加载600N、2200N、3800N、5400N、7000、8600N、11100N,依次进行仿真,详细结果记录到表1中。

图3 不同壁厚对管件轴向和径向变形的影响

表1 不同壁厚的仿真结果对比
3 壁厚与对截面影响的实验
按如图所示实验,对壁厚分别为2mm和3.5mm的薄壁管件,其压头分别加载600N、2200N、3800N、5400N、7000、8600N、11100N 的力,传感器 1、3 测量的是Y向的变形,传感器2测量的是X向的变形,逐步记录实验结果,记录实验结果如表2所示。
通过仿真和实验结果发现,管件的轴向弯曲实验和仿真的符合度非常好,而截面的扁化变形仿真结果要比实验明显大一些,误差最大有0.2mm。产生误差的主要原因是因为仿真的材料参数和实验的材料参数有一定的差别,而仿真的数据比较理想化。
对比壁厚为2mm和壁厚为3.5mm的管件,发现前者的轴向屈曲和截面变形明显比后者要大。主要是由环形截面的惯性矩和截面的抗弯模量差异导致,壁厚3.5mm的管件的截面惯性矩和抗弯模量均为壁厚3.5mm的管件的截面惯性矩和抗弯模量的1.75倍。
当载荷达到8600~11100N时,薄壁管件已经进入塑性变形阶段。通过对上述结果分析,可以得到以下结论:
(1)壁厚是影响薄壁管件在校直过程中截面变形的非常重要的因素。当薄壁管件的直径相同时,壁厚越大,管件的截面变形越小,截面越不容易变形。
(2)厚壁管在弯曲过程中截面都可以假设不发生变形。而对于薄壁管的校直问题,截面变形必须考虑。
(3)若管件的变形只是停留在弹性弯曲阶段,这时管件发生弯曲的残余变形可以忽略不计。

图4 薄壁管件的校直实验示意图
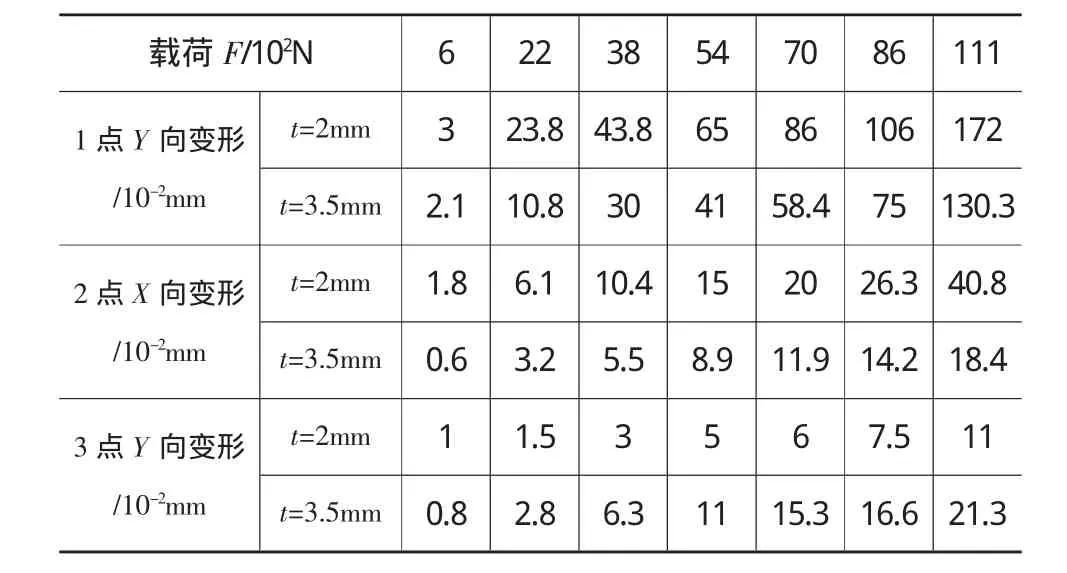
表2 不同壁厚的实验结果
4 总结
本文基于弹塑性理论分析薄壁管件校直过程中的截面变形的问题,通过仿真研究了管件截面变形与壁厚的关系,并用实验方法验证。通过对以上的研究分析表明,壁厚是影响薄壁管件截面质量非常重要的因素,在实际校直工作中必须加以考虑。
[1]E.M.M.Fonseca,F.J.M.Q.deMelo,Numerical solution of curved pipes submitted to in-plane loading conditions[J].Thin-Walled Structures 48(2010)103-109.
[2]E.M.M.Fonseca Determination of flexibility factors in curved pipes with end restraints using a semi-analytic formulation,International Journal of Pressure Vessels and Piping 79(2002)829-840.
[3]Kevin Weicker,Shell analysis of thin-walled pipes.Part I Field equations and solution[J].International Journal of Pressure Vessels and Piping,2010,87(2010)402-413.
[4]余同希,章亮炽.塑性弯曲理论及其应用[M].北京:科学出版社,1992:365-368.
[5]浦广益.ANSYS Workbench 12[M].北京:中国水利水电出版社,2010:193-193.
[6]钟华勇.锆合金薄壁管件三点弯校直中的截面扁化[J].塑性工程学报,2011,18(4):97-100.
[7]李林业,陈绳德,柴庭福.薄壁管的无芯弯曲.锻压装备与制造技术,1992,27(3).
[8]张 鹏.薄壁方管激光弯曲过程的模拟研究.锻压装备与制造技术,2006,41(1).

