具有两种运动模式的球形机器人动力学建模与设计

赵 伟，孙汉旭，贾庆轩，张延恒，于 涛

（北京邮电大学 自动化学院，北京 100876）

球形机器人是一种结构全封闭，控制系统、电机和电源模块都包含在作为运动机构的球形外壳内部的移动机器人［1］。它以结构简单、不存在倾倒问题、零转弯半径、运行效率高等优点受到国内外学者的关注［2-3］。

目前已有的球形机器人都是依靠重心的改变进行驱动。爬坡能力取决于重摆所占比重，重摆比重越大爬坡能力越强［4］，但是重摆所占比重过大会导致球形机器人运载能力下降。目前已有的球形机器人重摆所占比重均不超过25%，爬坡能力均在15°以下。

针对此问题，本文设计了一种具有新型连杆爬坡机构的球形机器人（BYQ－X），该球形机器人除了传统的重摆行走方式之外，还可以利用新型运动机构通过电机直接驱动球壳运动。新机构具有较强的爬坡越障能力，球形机器人在平面地形利用重摆行走，此时球形机器人没有被动摩擦轮，摩擦力完全提供动力，运行时能量利用效率高，机器人可以全向运动［5-6］；当球形机器人需要爬较大坡度的时候，球形机器人利用连杆机构进行爬坡。此时，球形机器人伸出两根连杆，连杆与电机定子固连，球体与电机转子固连，球形机器人运动不依赖重摆重力，通过电机直接驱动球壳运动，此状态下的球形机器人具有较强的爬坡能力。

1 BYQ－X的总体结构

1.1 运动驱动部分

BYQ－X的总体结构分为运动驱动部分、伸缩连杆部分2个子系统。其沿用了球形外壳作为运动机构。BYQ－X具有两种运动状态：①球壳封闭，如图1所示，所有机械和控制系统包含在球壳内部，通过重摆的转动改变重心，驱动球体全向运动；②两侧的连杆伸出，如图2所示，连杆末端两个轮子支撑在地面上，电动机直接驱动球体移动。

如图1所示，当球壳处于封闭状态时，球壳两侧的轴承支撑可旋转内框，电机1固定于内框上，与电机1转轴相连的齿轮1与固定在球壳上的外环齿轮啮合。电机1可驱动内框绕X轴旋转，由于重摆安装在内框上，相当于电机1驱动重摆绕X轴旋转。电机2固定于内框上，通过链轮与链条的组合，驱动两块重摆绕Y轴旋转。通过两个电机的驱动，可以实现BYQ－X在水平面内全向滚动。此状态下BYQ－X的结构与传统球形机器人相似，其运动学和动力学模型也具有相似性［7－8］。

图1 球形机器人未伸出连杆状态下的结构示意图Fig.1 Spherical robot’s fold status

如图2所示，当BYQ－X处于连杆伸出状态时，两个连杆分别从球体的两侧伸出，连杆末端的轮子与地面接触。当电机1驱动内框相对于球壳转动时，由于连杆与内框固连，连杆也会相对于球壳沿相同方向转动，此时地面会阻止连杆的运动趋势，由于反作用力，球壳将会沿反方向转动，地面对球体的摩擦提供向前的动力，球体将会向前滚动。此时的运动模式相当于电机1直接驱动球体滚动，驱动力矩的大小取决于电机输出力矩的大小，而不受重摆大小的影响，可以大大增加球体的爬坡能力。

图2 球形机器人伸出连杆的状态Fig.2 Spherical robot’s unfold status

1.2 连杆部分

BYQ－X有两个连杆，每个连杆由2个移动副、一个转动副和一个轮子组成，如图3所示。

连杆分4段，材料是铝管。固定环1和固定环2将关节1固定在内框内壁上，关节2套进关节1内部，并通过丝杠传动配合。固定在关节1上的1号电机驱动啮合在丝杠底端的齿轮，从而驱动关节2伸缩。关节2的顶端固连着球壳盖，当连杆缩回球体内部时，球壳盖起到密封保护的作用。2号电机固定在关节2上，通过锥齿轮传动，驱动关节3旋转。关节2与关节3之间还安装了制动器，可以将关节2与关节3之间的旋转夹角锁死在某一个角度。关节4与关节3也是通过丝杠传动配合，通过固定在关节3上的3号电机，驱动关节4伸缩。

图3 连杆示意图Fig.3 Structure of climbing link

球形机器人伸出连杆的步骤如下：关节2伸出，关节3转动90°，伸出关节4。

1.3 无线分布式控制系统

BYQ－X机械结构分为运动驱动部分，连杆部分等，这几个功能单元相对独立。因此控制系统也分为2个模块：运动驱动部分控制模块、连杆系统控制模块，如图4所示。

图4 控制系统结构图Fig.4 Structure of the control system

各个模块的安装位置、硬件组成和功能如下：

（1）运动驱动部分控制模块

安装于内框壁上，采用32位ARM7处理器AT91SAM7XC256作为主处理器，通过RF200无线传输模块接收人工控制台的指令和反馈机器人的工作状态，通过串口采集安装在内框上的惯性测量系统的角速度、加速度和欧拉角参数，并分别通过CAN总线与电机2通讯，串口RS232与电机1通讯，实现电机1和电机2的协调运动，完成BYQ－X的直线、曲线行走和静态平衡控制等功能。电机1采用MAXON电机RE50，驱动器EPOS 50／5；电机2采用MAXON直流无刷电机EC40，驱动器Elmo Solo Whistler。

（2）连杆系统控制模块

安装在内框外壁上，控制连杆电机和制动器，依次完成连杆伸缩定位和制动器的制动解锁等操作，同时可以采集连杆上限位开关和霍尔元器件的数据，进行协调控制。主处理器为32位ARM7处理器AT91SAM7XC256，通过IO口发送指令。每个连杆装有三个电机和一个驱动器，电机采用MAXON电机，小仓制动器，电机驱动器LMD18200T。

BYQ－X采用了分层式和模块化的软件系统，其中运功驱动部分控制模块采用了Linux操作系统，其上运行外部无线通信、CAN通信、串口RS232通信、运动控制算法、路径规划、资源分配等应用层任务，应用层各个任务统一由调度层进行调度，并通过各部件的传感器数据反馈信息进行协调控制。并通过Visual C＋＋6.0软件绘制操作界面。

2 力学建模与对比分析

爬坡能力是衡量移动机器人工作能力的主要性能指标之一［9］。球形机器人应用在野外环境时不可避免地会遇到爬坡和越障等问题。本节将详细分析手臂伸出时的新型机器人与传统球形机器人的爬坡能力。

2.1 连杆未伸出时的爬坡能力分析

传统球形机器人的驱动力矩来源于机器人重心偏离形心而产生的偏心力矩［10-11］。重摆通常所占比重不超过球形机器人自身质量的25%，据此计算其最大爬坡能力可以得到为0.2527rad，即14.49°。

图5 传统球形机器人爬坡ADAMS仿真模型Fig.5 Simulation of traditional spherical robot climbing slope by ADAMS

用ADAMS软件对此计算结果进行验证，如图5，在ADAMS中设置一个转动的平面，用PRO－E设计出球形机器人模型，导入ADAMS。设定参数R＝0.5m，μ＝25%，让机器人在此平面上前进，当球体加速度为0时，认为达到最大爬坡角度。最终得到不管摩擦因数如何改变，其爬坡能力都小于等于0.2527rad（14.49°）。

2.2 连杆伸出后静力学建模

当两个手臂展开后，重摆的位置将不再改变，此时球形机器人爬坡时的力学简化模型如图6所示。整体分为球体、连杆、后轮三个部分，可以将两个连杆和后轮合为一个连杆和后轮进行分析。其中α为坡面坡度，θ为连杆与地面（坡面）的角度，Gq是球体的重力，Gh为小轮的重力，Gg为连杆重力。Fm为球体受到的地面摩擦力，f为两个小轮受到的摩擦力。Nq、Nh分别为球体和后轮受到的坡面支持力。这两个力是由多个力合成的。

图6 机器人利用爬坡机构爬坡的受力分析图Fig.6 Force analysis of robot climbing slope by climbing link mechanism

首先对连杆进行受力分析，如图7所示，其中Gg为连杆重力，N为小轮提供的垂直支持力，相应地，连杆的另一端与球体连接的轴上，会受到大小相同、方向相反的一个力，两个力形成的力偶与电机输出的力矩T相平衡。相应地Fq与Fh分别为球体和小轮对连杆的力沿连杆方向的分量。

图7 连杆的受力分析图Fig.7 Force analysis of climbing link

Fh为连杆与小轮沿连杆方向的相互作用力。此时小轮向下的压力等于小轮自身重力加上连杆对小轮垂直方向的分力之和。

将连杆两端受到的力分解为沿杆方向的力和垂直于杆方向的力，在受力平衡状态下，沿连杆方向和水平方向的合力为0，对连杆的合力偶也为0，kq为前轮的静摩擦因数，设δq和δh分别为球体和小轮的滚动摩阻，R为球体半径，r为小轮半径。得到关于坡面最大牵引力即坡面摩擦力Fm的公式为

为求最大爬坡角度α，给出下列相关公式：

联立式（1）～（5），即可解出最大爬坡角度α。

2.3 连杆伸出后动力学建模

为了实现对机器人的有效控制，本文基于拉格朗日方程建立连杆伸出后的动力学模型［12］。

机器人开始爬坡的出发点为O，建立坐标系，如图8所示。

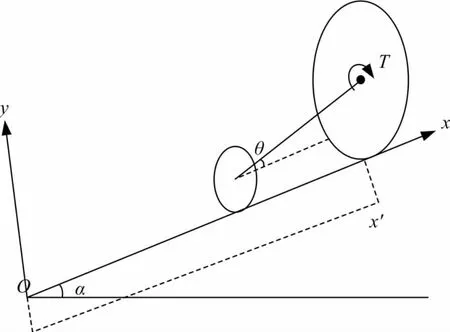
图8 新机构爬坡动力学模型Fig.8 Dynamic model of Robot climbing slope by climbing link mechanism

机器人沿坡面做直线运动，取x为广义坐标，球体半径为R，后轮半径为r，杆长为l，机器人的出发点O为势能零点，球体滚过的角度为θq，后轮滚过的角度为θh。θq，θh与x有以下关系：

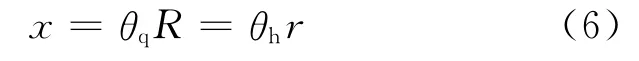
系统在任意位置的势能为

式中：Jq和Jh分别为球体与后轮的转动惯量，表达式为

系统的拉格朗日函数为

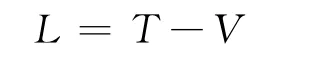
假设该坡度小于机器人最大爬坡角度，即机器人可以沿坡面向上运动，球体与后轮作纯滚动，则作用在机器人上的主动力为机器人重力与电机驱动力矩。

根据虚功原理得到系统广义力为

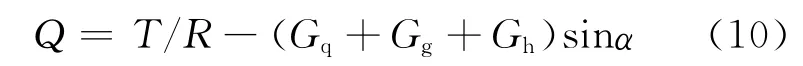
将式（7）～（9）代入拉格朗日方程，可得连杆伸出状态下的动力学方程为

由式（11）可见，机器人在小于其最大爬坡角度的坡面上将做加速运动。当机器人刚启动时输出力矩达不到额定值，机器人加速度会较小，而随着电机力矩T逐渐增大，其加速度将越来越大，最终当T达到额定值时，机器人以恒定的加速度沿坡面向上运动。

2.4 连杆伸出后爬坡能力仿真分析

首先用Matlab对新机构爬坡能力公式进行仿真，设定参数Gq＝100N，Gh＝5N，δq＝0.01，δh＝0.01，θ＝30°，R＝0.5m，r＝0.1m。

得出机器人最大爬坡角度α与前轮静摩擦因数kq的关系曲线如图9所示。

图9 爬坡角度与摩擦因数关系曲线Fig.9 Relationship between climbing angle and friction coefficient

用Adams软件对由Matlab计算所得到的曲线进行验证，如图10。在ADAMS中设置一个坡度逐渐增大的转动平面，用pro－E设计新型机器人模型，将其导入ADAMS。设定参数，让机器人在此平面上前进，当球体加速度为0时认为达到最大爬坡角度。

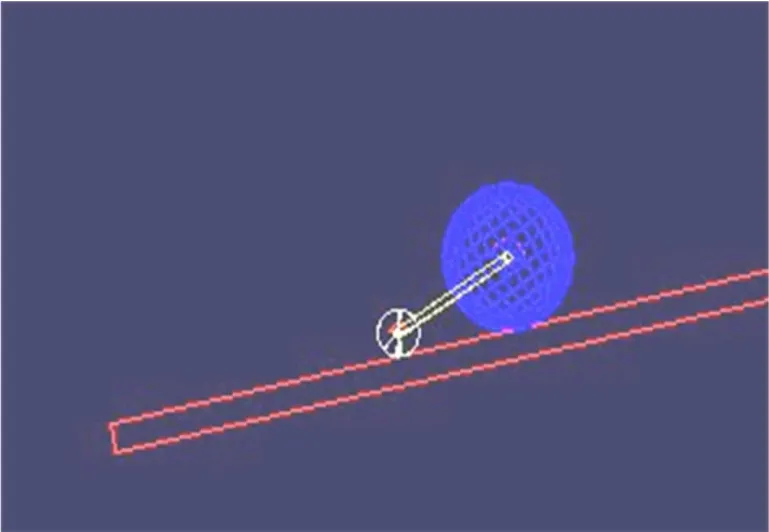
图10 新机构爬坡ADAMS仿真模型Fig.10 Simulation of new spherical robot climbing slope by ADAMS

改变球体与坡面间的摩擦因数，由此得到一系列表示摩擦因数k与对应最大爬坡角度α的点（爬坡能力（rad），摩擦因数）为：（0.14，0.2），（0.2，0.3），（0.25，0.4），（0.3，0.5），（0.34，0.6），（0.38，0.7），（0.41，0.8）。将这些得到的点进行曲线拟合，得到如图11所示的曲线。将拟合得到的曲线与图9中Matlab计算得到的曲线相比较，可见两条曲线几乎完全重合。因此验证了力学模型的正确性。与传统球形机器人的爬坡能力比较结果如图12所示。图12中，横线为传统球形机器人的重摆比重为25%时可以达到的最大爬坡角度。曲线为新型机器人爬坡弧度随摩擦因数的变化曲线。由此图可见，当摩擦因数达到0.41之后，新机构可以显著提升球形机器人的爬坡能力。

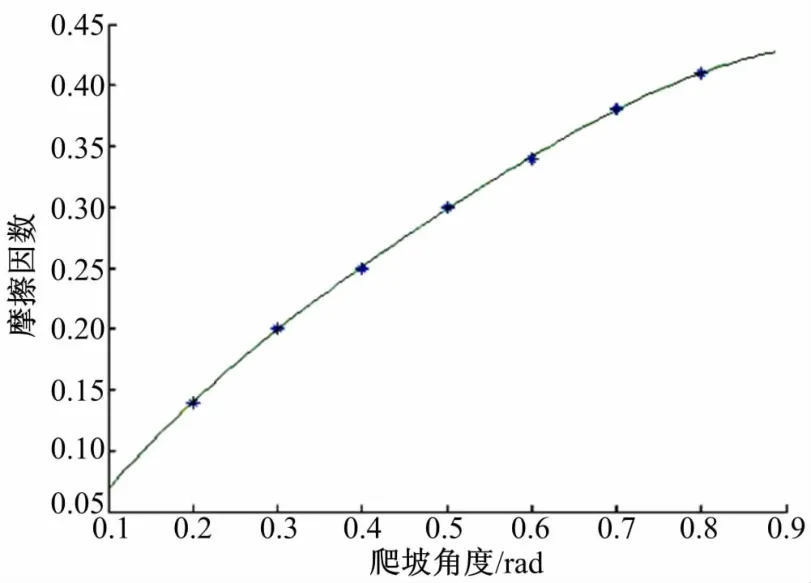
图11 爬坡角度与摩擦因数关系拟合曲线Fig.11 Curve of relationship between climbing angle and friction coefficient made by Matlab curve－fitting

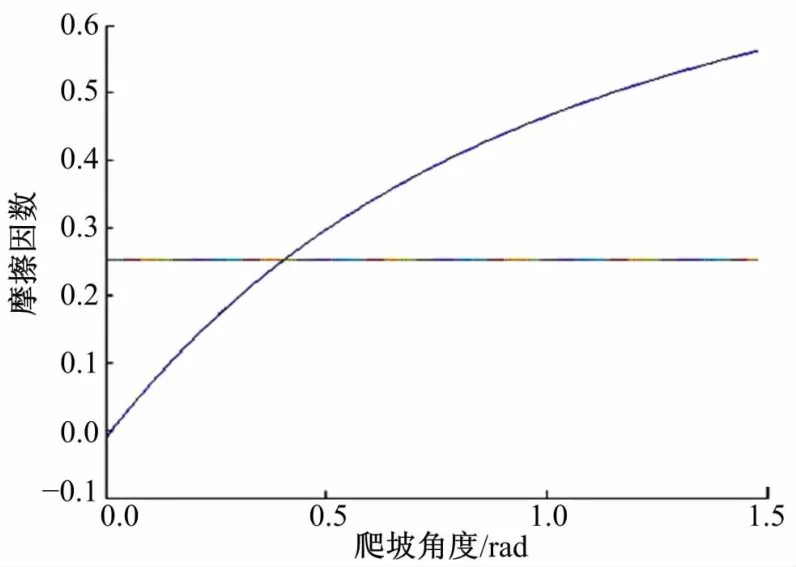
图12 新旧球形机器人爬坡角度比较图Fig.12 Compare of the climbing angle between new and traditional spherical robot

根据实际测量，球形机器人外壳与混凝土路面、压实土壤路面的滑动摩擦因数分别为0.73和0.92，均远大于0.41，因此在野外路况下新机构可以有效提高球形机器人的爬坡能力［13］。

3 新型机构的优化设计分析

由得到的曲线可以看出，新型机构球形机器人的爬坡能力与球体、坡面之间的摩擦因数有关。摩擦因数越大，爬坡能力越强。从最大爬坡角度公式可以看出，影响最大爬坡角度的参数除了前轮摩擦因数之外还有很多。当球体材料与路面情况确定的时候，前轮摩擦因数、球体与小轮的滚动摩阻都是确定的。球体大小R有限制。要增强新型机构的越野能力，使其达到最大爬坡角度，需要对小轮半径r、球体重量和连杆长度l进行优化设计。

首先分别对3个参数对爬坡角度的影响进行仿真分析。

设定摩擦因数为0.5，球体重力设定为100 N，球体半径R为0.5m，连杆长度l设定为2m，分别用Matlab与ADAMS两种仿真软件得到r与爬坡角度之间的关系如图13所示。

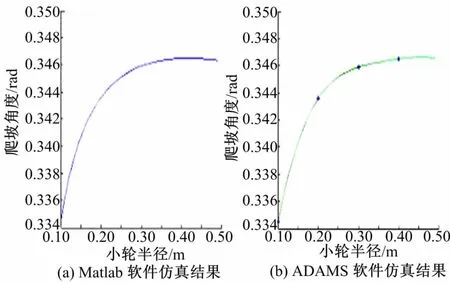
图13 爬坡角度与小轮半径关系曲线Fig.13 Relationship between climbing angle and radius of the wheels

由图13可见，两种软件得到的曲线基本一致，从而验证了所得曲线的正确性。小轮半径r从0.1m到0.5m之间变化，爬坡角度在0.334 rad到0.348rad之间变化。影响不大，因此对小轮半径进行优化意义不大。

固定小轮半径r为0.1m，分别用Matlab和ADAMS两种仿真软件得到杆长l与爬坡角度的关系如图14所示。

图14 爬坡角度与连杆长度关系曲线Fig.14 Relationship between the climbing angle and the length of the climbing link

由图14可见，两种软件得到的曲线基本一致，从而验证了所得曲线的正确性。杆长从1m到10m之间变化，爬坡角度变化趋势是先增加后减小，由于杆本身具有一定重量，因此如果太长，球体爬坡能力反而下降。

固定杆长为2m，球体重力与爬坡角度的关系如图15所示。

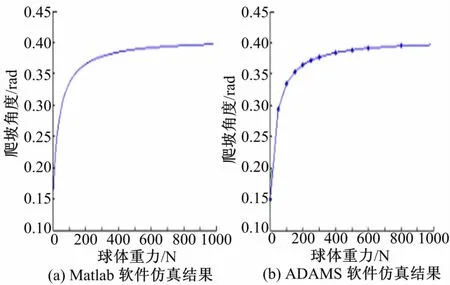
图15 爬坡角度与球体重力关系曲线Fig.15 Relationship between the climbing angle and the weight of the spherical

由图15可见，两种软件得到的曲线基本一致，从而验证了所得曲线的正确性。球体重力从0到1000N变化，爬坡角度变化趋势是一直增大的，但是超过300N之后，增大趋势越来越缓慢。

由得到的曲线可以看出，重力越大球形机器人爬坡能力越强，杆长与爬坡能力的关系是类似抛物线的关系，综合二者对爬坡能力的影响，得到如图16所示的等高线图。

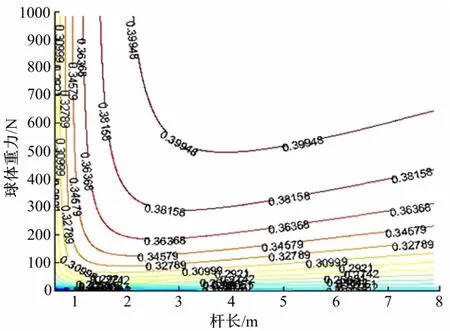
图16 杆长与球体重力对爬坡能力的影响Fig.16 Influence to the climbing angle by the length of the climbing link and the weight of spherical

等高线上的数字是爬坡弧度。由图16可见，对应于球体每一个重力值，都有一个使其爬坡角度达到最大值的最佳杆长。最佳杆长与球体重力的关系由Matlab计算得出，曲线如图17所示。可见，球体重力超过100N之后，杆长越长越好。因此在设计中，杆应当尽量长。

4 实 验

BYQ－X的实验包括系统测试和性能测试两部分。性能测试主要测试机器人的通讯、运动、功耗等单项性能；系统测试时在保证机器人各单元及系统可靠运行的前提下，对机器人的协调运动进行整体实验。

图17 不同球体重力对应的最佳连杆长度Fig.17 The best length of the climbing link for each weight of spherical

4.1 系统测试

系统测试时，人工控制台采用笔记本电脑，其上安装VC＋＋开发的控制界面，通过RF200无线数传模块与机器人建立通信网络，将前进、后退、转向、手臂展开等遥控指令发送给BYQ－X，控制机器人的运动。

在本测试中，机器人由全封闭状态开始，两端连杆关节2完全伸出，关节3展开90°，关节2再次收回到球体内，关节4伸出，直至轮子与地面接触，完成变形动作。整个流程如图18所示。

图18 BYQ－X变形全过程Fig.18 The process of BYQ－X transform

4.2 性能测试

经测量，BYQ－X的主要性能指标为：质量为70kg，直径为630mm，最大通讯速率为11Mbit／s，最大运行速度为0.5m／s。

如图19所示，以木板搭建坡面，上面铺上橡胶从增大摩擦因数，以模拟野外摩擦因数较大的压实土壤路面、混凝土路面等情况［14］，测得搭建实验坡面与球壳的摩擦因数为0.91，根据前文所得公式计算出BYQ－X封闭状态爬坡角度应该为14°，连杆伸出后最大的爬坡角度为25°。

分别对机器人手臂未伸出和伸出后进行爬坡运动实验，如图19所示，设定坡的角度为0°～30°，采用开环控制方式，电动机经过齿轮减速后的输出力矩为T＝21.2Nm。电机采用MAXON公司生产的有刷直流电机，驱动器采用ELMO驱动器，可以实时读取电机转速与输出力矩。本文对本项目球形机器人两种状态下沿斜坡的直线运动分别进行了4组试验。每次试验记录下在不同坡度上运动5s的情况。

由表1记录的实验数据可以看出，连杆伸出状态下BYQ－X机器人并不是匀速运动。第1s运动距离较短，之后比较稳定，这是因为刚开始时电机还没有达到给定输出。

图19 BYQ－X爬坡实验Fig.19 The climbing experiment

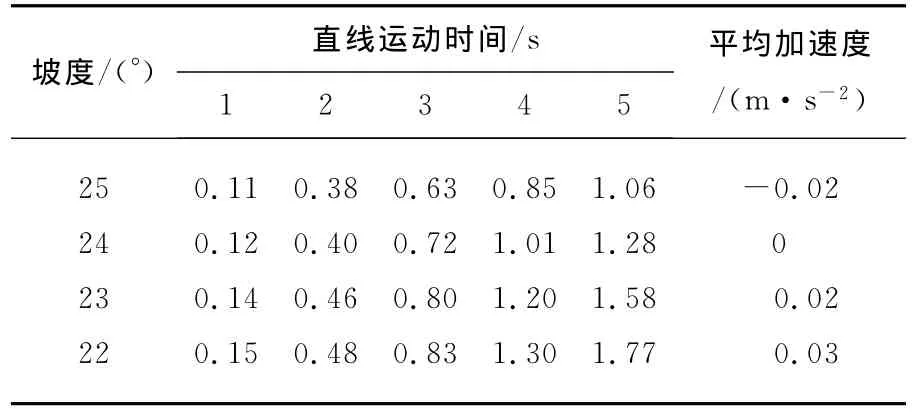
表1 BYQ－X机器人连杆伸出状态爬坡距离／mTable 1 Experiment data of BYQ－X in unfold status

机器人在爬24°以下坡面时为加速运动，在24°以上坡面为匀速运动。当坡度为25°的时候，BYQ－X机器人还是可以向上运动，但是运动是减速的，这说明机器人在此之后受力方向是沿坡面向下的，但是还是在向上运动，这是由于机器人初始状态受到静摩擦力的一刻获得了一定的动能，之后只是靠初始速度进行“冲坡”，因此速度越来越慢。而到了更大角度26°的时候机器人只能在坡面上静止，之后就开始向下滑。由此可见连杆伸出状态的机器人的爬坡能力为24°。

由表2记录的实验数据可以看出，封闭状态下BYQ－X机器人第1s运动距离更短，之后趋于稳定，这是因为刚开始时电机还没有达到给定输出，重摆摆起也较慢，系统反应时间更长。

机器人在爬13°以下坡面时为加速运动，在13°以坡面上为匀速运动。当坡度为14°的时候，BYQ－X机器人还是可以向上运动的，但是速度开始越来越慢。而到了15°的时候机器人能在坡面上静止，之后开始向下滑。由此可见封闭状态的机器人的爬坡能力为13°。

测得的试验结果得到，连杆伸出状态机器人爬的最大坡度为24°，封闭状态下机器人的最大的爬坡角度为13°。

表2 BYQ－X机器人球体封闭状态爬坡距离／mTable 2 Experiment data of BYQ－X in fold status

4.3 实验结果分析

通过实验可以得到以下结论：

（1）系统测试成功，机器人可以完成变形动作。

（2）连杆爬坡机构可以有效提高球形机器人的爬坡能力。

（3）性能测试中得到的爬坡角度都十分接近于理论计算值。进一步验证了力学模型的正确性。但数值都低了大约1°。其中连杆伸出状态误差率4%，封闭状态误差率6%。究其原因，主要是由于机构内部摩擦阻力造成的影响。其次由于封闭状态误差较大是因为重摆形状不规则，其提供的力矩计算值偏大。

5 结束语

提出了一种具有连杆爬坡机构的新型球形机器人，建立了机器人爬坡的力学模型，并对此模型进行了仿真验证与分析优化，以此为依据设计制造出了具有能够有效提高爬坡能力的连杆机构的球形机器人BYQ－X，并对该机器人进行了实验。该机器人在封闭状态下能实现全方位高效运动。连杆伸出状态下能够爬较大的坡度。使得球形机器人可以在野外复杂地形条件下应用，大大扩展了球形机器人的应用范围。目前本机器人连杆伸出的时候无法实现转弯，但是在两个小轮上加装电动机就可以实现变形后的转弯运动。

［1］肖爱平，孙汉旭，廖启征，等.一种球形机器人的设计与原理分析［J］.机电产品开发与创新，2004，17（1）：14－16.Xiao Ai－ping，Sun Han－xu，Liao Qi－zheng，et al.The design and analysis of a spherical mobile robot［J］.Development ＆Innovation of Machinery ＆ E－lectrical Products，2004，17（1）：14－16.

［2］Ranjan M J，Mark A M.A simple motion planner for a spherical mobile robot［C］∥Proc IEEE／ASME，International Conference on Advanced Intelligent Mechatronics.Atlanta：IEEE Press，1999：19－23.

［3］Amir H J A，Puyan M.Introducing august：a novel strategy for an omnidirectional spherical rolling robot［C］∥Proc IEEE，International Conference on Robotics ＆Automation.Washington：IEEE Press，2002：3527－3533.

［4］Ranjan M，Mark A M，Jay T P.Motion planning for a spherical mobile robot：revisiting the classical ball－plate problem［J］.Transactions of the ASME，2002，124：502－511.

［5］王亮清，孙汉旭，贾庆轩.球形机器人的爬坡与弹跳能力［J］.北京邮电大学学报，2007，30（2）：11－14.Wang Liang－qing，Sun Han－xu，Jia Qing－xuan.Research on the climbing and jumping of a spherical rolling robot［J］.Journal of Beijing University of Posts and Telecommunications，2007，30（2）：11－14.

［6］方琛玮，庄未，刘晓平，等.基于ADAMS的球形机器人的运动学分析［J］.机械工程与自动化，2009，2（1）：118－119.Fang Chen－wei，Zhuang Wei，Liu Xiao－ping，et al.Kinematics simulation of a spherical robot with arms based on ADAMS［J］.Mechanical Engineering ＆Automation，2009，2（1）：118－119.

［7］赵凯亮，孙汉旭，贾庆轩，等.基于ADAMS的球形机器人加速特性分析［J］.机械设计，2009，7（7）：25－27.Zhao Kai－liang，Sun Han－xu，Jia Qing－xuan，et al.Kinematics simulation of a spherical robot［J］.Journal of Machine Design，2009，7（7）：25－27.

［8］Alizadeh H Vahid，Mahjoob M J.Quadratic damping model for a spherical mobile robot moving on the free surface of the water［C］∥2011IEEE International Symposium on Robotic and Sensors Environments （ROSE）.École Polytechnique de Montr Montreal，QC，Canada：IEEE Press，2011：125－130.

［9］Noppadol Chadil，Marong Phadoongsidhi，Kawee Suwannasit，et al.A reconfigurable spherical robot［C］∥2011IEEE International Conference on Robotics and Automation.Shanghai，China：IEEE Press，2011：2380－2385.

［10］Hashem Ghariblu，Hadi Mohammadi.Structure and dynamic modeling of a spherical robot［C］∥20128th International Symposium on Mechatronics and Its Applications（ISMA）.Sharjah，UAE，2012：1－5.

［11］Mikhail Svinin，Akihiro Morinaga，Motoji Yamamoto.On the dynamic model and motion planning for a class of spherical rolling robots［C］∥2012IEEE International Conference on Robotics and Automation.Saint Paul，Minnesota，USA，2012：3226－3231.

［12］Erkan Kayacan，Erdal Kayacan，Herman Ramon，et al.Adaptive neuro－fuzzy control of a spherical rolling robot using sliding－mode－control－theory－based online learning algorithm［J］.IEEE Transactions on Systems，Man，and Cybernetics－part B：Cybernetics，2012，99：1－10.

［13］Duvar R，Gokbayrak A B，Aytekin H S，et al.Real time control of tyre profiles using computer vision approach［C］∥Signal Processing and Communications Applications Conference（SIU）.Mugla，Turkey.IEEE Press，2012：1－4.

［14］Tannoury C El，Plestan F，Moussaoui S，et al.A variable structure observer for an on－line estimation of a tyre rolling resistance and effective radius［C］∥201212th International Workshop on Variable Structure Systems（VSS）.Nantes，France.IEEE Press，2012：167－172.