用于电能质量分析的电弧炉仿真模型
张峰何新杨丽君
(1.燕山大学电气工程学院,河北 秦皇岛 066004;2.承德供电公司,河北 承德 067000)
技术的飞速发展也带动了炼钢工业的飞速前进,同时也对炼钢工业提出了更高的要求,因此,作为炼钢工业重中之重的电弧炉就引发了人们越来越多的关注。由于电弧炉在炼钢过程中所表现出的强烈随机性和时变性,它成为了对电力系统提出更高要求的重要负荷。
尤其是在炼钢的熔化期,因电弧燃烧的过度不稳定,炉料坍塌,以及电极调节器的调节滞后等问题,会引发电力系统的诸多电能质量问题,其中又以电弧炉产生的谐波对电网影响最大,电压波动,电压闪变,三相不平衡等,归根结底都是由于谐波造成的。因此建立电弧炉谐波仿真模型对于研究电弧炉与电能质量的关系至关重要。
我国在20世纪80年代后期曾经有一段时间对电弧炉的关注度很高,因此也涌现出了非常多的优秀电弧炉模型,但后来因为诸多技术方面的困难以及理论发展的限制,对电弧炉模型的研究逐渐停滞下来。
不过,在科技发展飞速的今天,电网未来必将面临来自各方面的挑战,电弧炉作为对电网影响巨大的非线性时变电阻的一员,对它的研究是不得不进行的一项任务,通过对电弧炉的研究,我们可以了解更多类似于此的严重影响电网工作的各种设备。所以,电弧炉的研究依旧任重而道远,需要我们更加努力。
描述电弧炉的动态模型可分为“物理数学”模型和“黑箱”模型两大类,而对于电气行业来说,电弧炉的外特性则更为重要,所以因“物理数学”模型的过分繁琐和“黑箱”模型的简单直观,“黑箱”模型得到了很好的发展。根据文献[1],目前建立起来的黑箱模型有:非线性电阻,非线性时变电阻,能量平衡模型,基于神经网络和模糊逻辑的电弧模型,基于混沌理论的电弧模型,谐波电流源或谐波电压源。
文献[2-5]把电弧炉看成非线性时变电阻,文献[6-7]根据能量平衡关系建立了电弧炉电阻模型,文献[8]按照分段线性化的方法建立了电弧炉模型,文献[9-11]建立了电弧炉的混沌模型,文献[12]运用蔡氏电路调制电弧炉半径,得到混沌模型,但是并未进行Matlba仿真,文献[13]改进了蔡氏电路,并用改进后的混沌信号对分段电弧炉模型进行了调制,文献[14-15]提出了根据实时测量所得的数据进行仿真的方法。
本文即在Matlab环境下,搭建了电弧炉的谐波模型。第一种把电弧炉当做谐波电流源,用多种随机变化的特定次谐波源叠加合成,这种模型简单明了,而且能非常直接的反应电弧炉的谐波特性,并且更好的突出电弧随机性。第二种在刘小河非线性时变电阻模型的基础上引入能量变化关系,通过对原有模型的改进,力求模型更加精确。第三种在电弧炉半径上叠加混沌信号,搭建其混沌模型。
1 谐波源模型
电弧炉引起的谐波电流成分主要为2~7次谐波[16]。因此,可以在Matlab/Simulink中分别建立2~7次谐波源,然后将这多种谐波源相互叠加,在叠加形成的新谐波源基础上再叠加白噪声信号和一个受限制的随机数信号发生器,以弥补2~7次谐波源以外的不足。为了使谐波的幅值能够随机变化,本文采用随机数信号发生器,通过控制电流源、测量模块和电感电容,将特定次谐波分别提取。

图1 幅值随时间随机变化的二次谐波源
图1中为幅值随机变化的二次谐波源,只要改变电感和电容的参数以及正弦信号发生器的频率,就可以分别实现幅值随机变化的3~7次谐波源。

图2 电弧炉谐波电流源仿真模型
图2中把2~7次谐波源叠加在了一起,再用频率为50Hz的正弦信号发生器代替电网电流波形。仿真结果如图3所示。
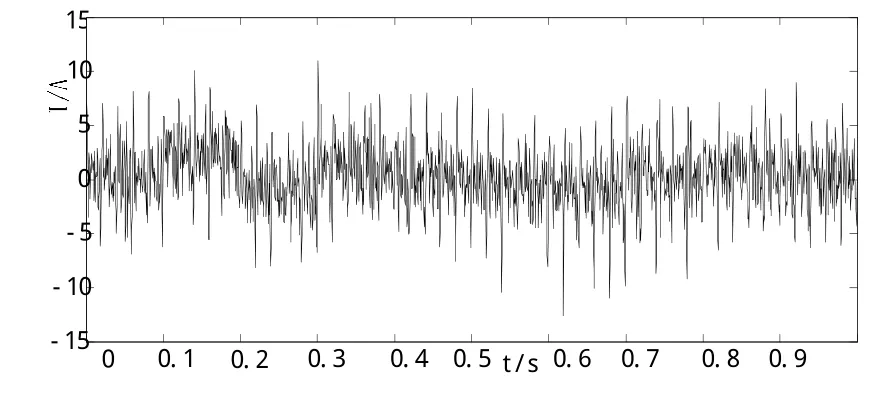
图3 电弧炉谐波源模型的仿真结果
图 3中纵轴表示电流大小,横轴为时间。图2中把电弧炉看成电流源的仿真模型,在应用时,只需把电流大小随时间变化的波形叠加到给电弧炉供电的电网中,就可以模拟实际效果,只是本文所给出的模型为了突出电弧炉的随机性,所得出的输出结果并不能真实模拟电流谐波的细致变化,但是它更好的反应了电弧的波动性。所以,此电弧炉谐波源仿真模型更适合用于电压波动的研究。
2 非线性时变电阻模型
2.1 公式说明
电弧炉的电弧能量方程为[17]

式中,i为电弧电流,r为电弧半径, k1,k2,k3,n,m为可变参数,它们的取值可以根据实际情况从相关文献中查出[18]。由能量公式,定义了电弧电导g =,故得出电弧电阻应该为R =。
从相关文献中可以查出一周期内电弧半径的变化情况,本文把这种变化近似认为是在正半轴以正弦规律波动[19],即r=,其中w=100π。因此可以由能量关系得出电弧炉随时间变化的关系

我们通常已知的电弧炉时变电阻模型是在3个理想条件下建立的[20],它主要反映了交流电弧的外特性,受到弧长等的影响。如式(3)所示。

式中,w为外加正弦电压激励的角频率,θ为电弧电流滞后电源初相的角度,D受电弧弧柱热惯性的影响。A,B ,C ,L 以及上述参数在文献[21]中都有详细介绍,这里不再一一赘述。
取式(2)和式(3)的平均值,可得

式(4)即为一个新的随时间变化的电弧炉电阻模型,此模型在原有基础上引入了更多的状态变量,考虑了更多电弧炉在炼钢过程中可能发生的变化,相当于同时考虑了外部与内部的变化,因此从理论上讲,要更精确。
2.2 模型仿真
以包头钢铁公司无缝钢厂的3t电弧炉为例,进行建模,首先,从相关文献中可以得知式(3)中的所有相关参数[21],再根据3t电弧炉的实际情况,可以从文献[18]中查出其余的相关参数。
图6即为式(4)在Matlab中搭出的仿真模型,图4为仿真出的电弧炉电弧电阻随时间变化的结果,图5为假定电弧两端电压为标准正弦波的情况下得出的电流波形。
为了模拟电弧电阻的非线性,分别在式(2)与式(3)的模型中加入了可以控制上下限的随机数信号发生器。
仿真发现在原有模型的基础上对电弧炉仿真模型进行改进是可行的。

图4 电弧炉电弧电阻随时间变化的仿真波形

图5 电弧炉电弧电流随时间变化的仿真波形
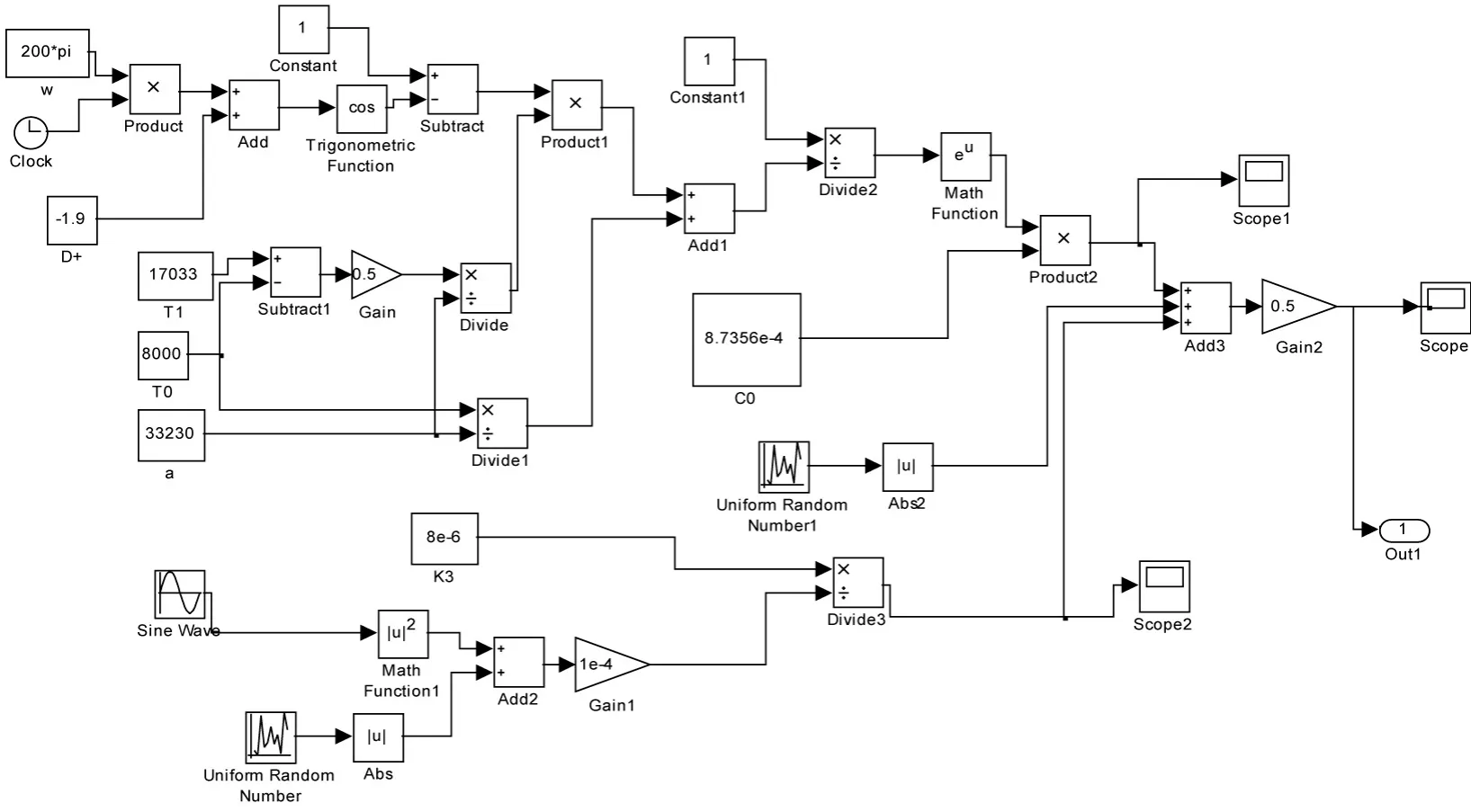
图6 电弧炉的非线性时变电阻仿真模型
3 混沌模型
3.1 理论分析
混沌模型是近年来兴起的一种新模式,大量研究表明,电弧炉的电压波动和闪变是混沌系统的外在表现,所以以往的以随机信号,噪声信号等研究电弧炉特性的方法正在冷却,而以混沌理论研究电弧炉的例子正在逐渐增多。
文献[12]首次提出以蔡氏电路产生的混沌信号去调制电弧炉的半径,然后通过文献[17]给出的电弧炉能量方程构建电弧炉模型,但是文献[12]给出的模型是用多组模拟电路搭建的,应用起来不大方便。文献[13]提出了对蔡氏电路的改进,在电弧炉线性分段模型的基础上提出了混沌模型,但是分段模型必须尽量多的进行分组才能很好的反应电弧炉的动态性能,这样就加大了建模的复杂性。所以本文在matlab基础上采用改进后的蔡氏电路对电弧半径进行调制,然后得出混沌电压源模型。
3.2 Matlab仿真
本文采用Matlab中的s函数进行仿真,采用已知的半径计算公式编写程序。篇幅所限,这里不再赘述,可参考文献[22]。

图7 电弧炉的混沌电压源模型
图7中,out1为改进后的蔡氏电路模块,文献[13]中已给出Matlab仿真模型,它的输出幅值是可以人为调节的。myarc_r为求电弧炉半径的s函数模块,myarc_Ron为根据电弧半径求电弧电阻的模块。
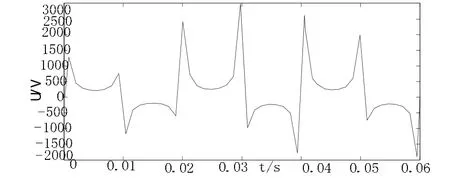
图8 电弧炉混沌仿真模型的输出电压波形
图8中纵轴表示电压大小,单位为V,横轴表示时间,单位为s。我们发现,混沌模型的输出波形与文献中给出的实际波形是非常相似的。
4 实用模型
对于电弧炉仿真来说,我们最终的目的还是为了将模型应用到实际研究中去,对于仿真模型来说,我们希望它能够满足两个要求,首先必须十分逼近真实情况,其次尽量使模型简单明了,尤其是在工程实际中,简单明了有时比逼真还要重要。
在工程实际中,最好的最适用的方法还是根据实际测量值来直接模拟电弧炉的工作情况。例如我们从文献中找出一组实际运行中的电弧炉熔化期所发出的谐波,发现其中2~7次谐波占主要地位。
2次谐波和3次谐波含量最大,平均值可达基波分量的5%~10%,最大可达15%~30%;4~7次谐波平均值为2%~6%,最大可达6%~15%[23]。仅根据以上所给出的大致数据我们就可以建立电弧炉的仿真模型。一般来说,取较大的谐波幅值,以便于研究对它的抑制方法。
假设基波的幅值为10kV,频率为50Hz,那么我们就可以分别取2次谐波幅值为1.5kV,3次谐波幅值为3kV,4次谐波幅值为1.5kV,5次谐波幅值为1.2kV,6次谐波幅值为0.9kV,7次谐波幅值为0.6kV,然后将这些波形直接叠加。

图9 可直接应用于工程中的简单电弧炉电压谐波源仿真模型
图9中,out1仍为改进后的蔡氏混沌电路,实际操作中完全可以不用这一环节,以便得到最简单最直接的仿真模型。

图10 电弧炉简单仿真模型的输出电压波形
显然,实用模型是能最简便最直接反应电弧炉谐波情况的模型。
5 结论
显然,无论是谐波源模型,非线性时变电阻模型,还是混沌模型等得出的仿真结果都是具有一定区别的,谐波源模型的优点在于能够非常直观的表示系统中由电弧炉引起的谐波,但是谐波源模型没有足够的时变性,以及准确无误表征电弧特性的优势。非线性时变电阻则很好的弥补了这些缺陷,但是电阻模型引入了过多参数,这些参数都要根据实际情况逐一确定,每一次工程实例的变动,都要进行参数的重新估算,繁琐程度比较高,这给工程领域的研究带来了很多不便。虽然最近兴起的混沌模型被很多人看好,它具有从本质上真实反映电弧特性的诸多优势,但作为新兴知识,混沌发生源本身依然还具有很多不足。
在本文最后提出了一种最简单的电弧炉谐波源模型,尽管它构造简单,也反映了电弧炉的谐波情况,但与实际还是有很大差距的。所以,我们不能简单的对任意一种电弧炉模型下定论,它们各有各的优点和适用范围。模型一可用于电压波动研究,模型二可用在谐波分析中,模型三则尚未广泛使用,而在实际工程工作中还是模型四比较适用。
现有的追求更高精度的电弧炉模型研究虽然取得了较大发展,而且给我们的研究工作带来了很多便利,但随着精度的不断提高,模型的复杂程度也在不断加剧,在工程实际中,这往往得不偿失。所以,如何根据实际情况,选择合适的电弧炉模型才是关键所在。
[1]单春贤,彭杰,等.基于动态电弧模型的交流电弧炉三相不平衡分析与控制[J].铸造技术,2011,32(2):234-238.
[2]张帆.炼钢厂电弧炉系统的谐波分析及治理措施仿真研究[D].广西:广西大学,2009.
[3]陈磊.电弧炉电气系统的建模与谐波分析[D].东北:东北大学,2008.
[4]刘小河,赵刚,于娟娟.电弧炉非线性特性对供电网影响的仿真研究[J].中国电机工程学报,2004,24(6):30-34.
[5]吕小东,刘小河.电弧炉电极调节器对电网电压波动影响的仿真研究[J].中国电机工程学报,2006,26(7):95-100.
[6]王琰,毛志忠,李妍,田慧欣,袁平.用于电压波动研究的交流电弧炉电弧模型[J].电网技术,2010,34(1):36-40.
[7]曹振.电弧炉电弧模型的研究[D].沈阳:东北大学.2009.
[8]王永宁,许伯强,李和明.电弧炉电气系统谐波电流仿真研究[J].华北电力大学学报,2005, 32(1): 28-31.
[9]ONEILL CATRILLO E, HEYDI G T, KOSTELICH E J.Nonlinear deterministic modeling of highly varying loads[J].IEEE Trans.on Power Delivery,1999,14(2): 537-542.
[10]OZGUN O, ABUR A.Flicker study using a novel furnace model[J]. IEEE Trans.On Power Delivery,2002,17(4): 1158-1163.
[11]MEDIANA A,GOMEZ-MANINEZ M A,FUERTEESQUIVEL C R. Application of bifurcations theory to assess nonlinear oscillations produced by AC electric arc furnaces[J].IEEE Trans.Power Delivery,2005,20(2):80l- 806.
[12]宁元中,梁颖,吴昊.电弧炉的混合仿真模型[J].四川大学学报,2005,37(1):85-89.
[13]王育飞,姜建国.用于电能质量研究的新型交流电弧炉混沌模型[J].中国电机工程学报,2008,28(10):106-110.
[14]许树楷,宋强,刘文华,童陆园.配电系统大功率交流电弧炉电能质量问题及方案治理研究[J].中国电机工程学报,2007,27(19):93-98.
[15]石新春,付超,马巍巍,周国梁.基于实测数据的电弧炉实时数字仿真模型及其实现[J].电工技术学报,2009,24(7):178-182.
[16]吕晓东,邹东等.电弧炉电气系统谐波分析的仿真研究[J].计算机与现代化,2009,166(6):71-77.
[17]王育飞,潘艳霞,姜建国.基于 Matlab的交流电弧炉随机模型与仿真[J].高电压技术, 2008, 34(5): 973-977.
[18]Chua L O. Introduction to nonlinear network theory[M].New York: Robert E Krieger Publishing Company, 1978.
[19]王晶,束洪春,等.用于动态电能质量分析的交流电弧炉的建模与仿真[J].电工技术学报, 2003, 18(3): 53-58.
[20]刘小河,程少庚,苏文成.电弧炉电气系统的谐波分析研究[J].电工技术学报, 1994,2(5): 21-26.
[21]郭继红,颜湘武.用于谐波分析研究的电弧炉系统的模型和仿真[J].继电器, 2005, 33(8): 31-32.
[22]王晶,翁国庆,张有兵.电力系统的Matlab/Simulink仿真与研究[M].西安:西安电子科技大学出版社.2008.
[23]翁利民,陈允平,舒立平.大型炼钢电弧炉对电网及自身的影响和抑制方案[J].电网技术,2004,28(2):65-67.

