基于形态-小波的行波差动保护的研究
田兴瑞 杨富宇 姚维为 董文静
(三峡大学电气与新能源学院,湖北 宜昌 443002)
超高压输电线路在输电网络中占据非常重要的地位。已有大量的电网选用超高压作为主干线路。传统的行波差动保护需要实时向对端传送大量故障信息,对传输通道有非常高的要求,使得保护在提高动作速度的同时降低了保护的可靠性。因此对行波差动保护可靠性的研究是一个极具意义的课题。
1 行差保护及其小波变换原理
1.1 行波差动保护原理
对图1所示的单相无损线路mn进行分析,用线路内部故障前后的电流、电压变化来说明行波差动保护的基本原理。线路上任意一点的电压和电流均可表示为
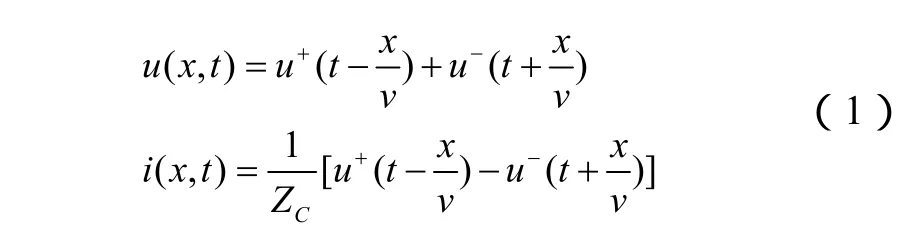

图1 单相无损线路示意图
当线路内部故障时,在图1(b)中F点发生故障,F点的电压、电流以 uF(t)、iF(t)表示,则
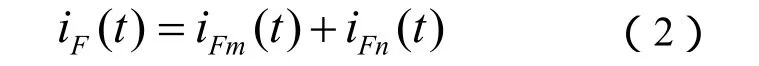
由图1(b)可写出下述两式


式中,τm由故障点F到m端的波行时间,τn由故障点F到n端的波行时间。
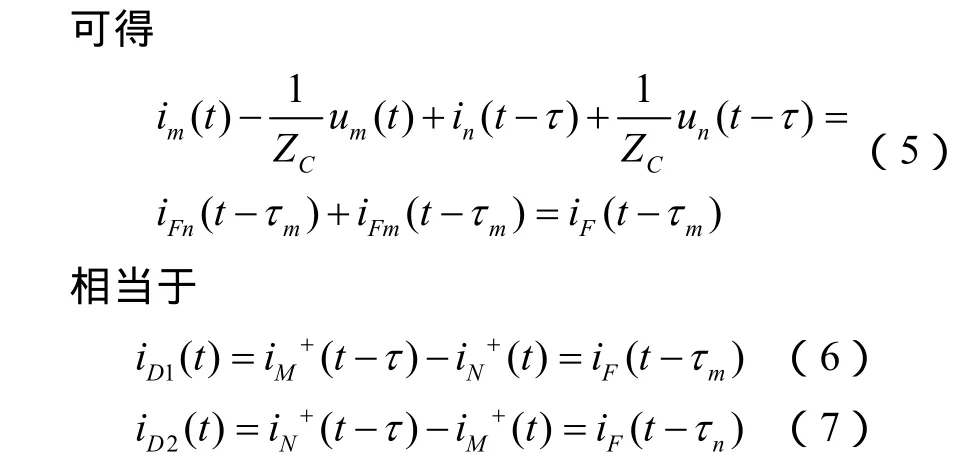
通过上述的分析,用 iD1(t)、iD2(t)可正确区分出线路内部、外部故障。当线路内部无故障时iD1(t) =iD2(t) =0,保护不动作;在线路内部故障时iD1(t)和iD2(t)为短路点的电流,保护动作。因此,iD1(t)和 iD2(t)可以作为行波差动保护的基本判据。
1.2 小波变换的定义
将小波基函数φ(t)平移τ后与被分析的信号x(t)在不同尺度下做卷积,这就是基础的小波变换。其准确定义为:设φ(t)为一平方可积函数(φ(t) ∈ L2(R)),如果该函数的傅里叶变换ψ(ω)满足条件

式中,称φ(t)为小波母函数(或基小波)。将母小波经过伸缩和平移后,就可得到一个小波序列。
2 基于形态-小波变换的行波差动保护方案
2.1 行波差动保护方案
当输电线路上发生故障时,会产生故障行波,定义母线到线路为正方向。如图2所示,当线路MN发生区内故障时,正向行波和反向行波同时到达两个测量端。线路MN两端的2倍正、反向电流行波为

式中,Zc=为波阻抗;和为分别为M端和N端正向行波,和为分别为M端和N端的反向行波。
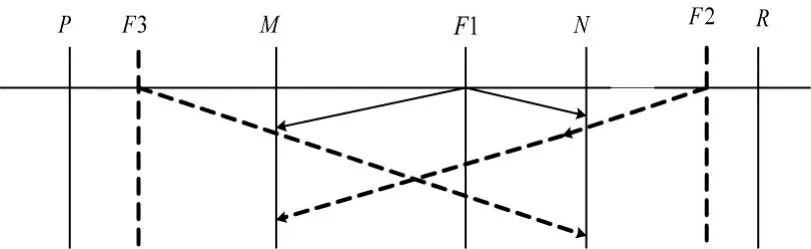
图2 故障行波网格图
当M端正方向区内发生故障,即F1点发生故障,M端和N端均提取反向行波波头,且两端的反向波头值相等。当M端正方向区外发生故障时,即F2点,N端提取到正向行波波头与M端提取反向行波波头大小相等,反向行波波头比正向正向行波波头延时τMN到达。同理当M端反方向区外发生故障时,即F3点故障,M端提取的正向波头值与N端提取的反向波头值大小相等,N端的反向行波波头比M端的正向行波波头延时τMN才到达。由此可以得出,无论是正方向区外还是反方向区外故障时,正向波头值比反向波头值提前τMN到达,把反向行波波头值延时τMN后与正向行波波头值相减所得值为0,而区内故障时没有这个特征,由此可以构成基于形态-小波变换的差动保护的方案。基于形态-小波行波差动保护方案的算法和主要步骤:
1)保护元件启动后,提取保护测量端的三相电压和电流,由于提取出的工频分量参杂有大量的噪声,用形态前置滤波器进行滤波。
2)从故障量中提取故障分量,对故障分量进行相模变换得到线模分量,计算出正、反向行波。当M端和N端只检测到正向行波而无反向行波时,本端采用正向模极大值;当同时检测到正反向行波时,M端和N端采用反向模极大值。
3)对上式中提取到的方向行波进行3层小波变换提取模极大值,并记录其对应时刻。将本侧提取到的模极大值及对应时刻传送到对端,同时也接受对端传来的数据。
4)调整方向波头值对应的时刻。如果本端提取的是反向行波波头模极大值,不管对端传来什么方向模极大值,都将对端传来的极大值延时线路波形时间τmn与本侧极大值进行下一步操作。如果本端提取的是正向行波波头模极大值,不管对端传来的值,都将本端的极大值延时τmn后与对侧传来的模极大值进行下一步操作。
5)对上一步调整时刻后的方向模极大值,进行下式的计算:

如果满足上式判为区内故障,不满足则判为区外故障。本文设定门槛值为δ=0.1。
2.2 基于数学形态学的行波差动保护方案
基于数学形态学的行波差动保护方案的算法和主要步骤如下:
1)保护元件启动后,提取保护测量端的三相电压和电流,由于提取出的工频分量参杂有大量的噪声,用数学形态学前置滤波器进行滤波。
2)从故障量中提取故障分量,对故障分量进行相模变换得到线模分量,计算出正、反向行波。当M端和N端只检测到正向行波而无反向行波时,本端采用正向行波;当同时检测到正反向行波时,M端和N端采用反向行波。
3)对上式中提取到的方向行波进行基于方向结构元素的形态梯度变换,并记录其对应时刻。
4)调整方向波头值对应的时刻。如果本端提取的是反向行波波头,不管对端传来什么方向的,都将对端传来的值延时线路波形时间τmn与本侧的值进行下一步操作。如果本端提取的是正向行波波头,不管对端传来的值,都将本端的值延时τmn后与对侧传来的值进行下一步操作。
5)对上一步调整时刻后的方向模极大值,进行下式的计算,即

3 仿真研究
本文使用如图所示的线路模型对基于小波变换的行波差动保护方案进行Matlab仿真。图中各线路长度如图所示,故障点Fl距离母线M距离为75km,故障点F2距离母线N距离为64km,故障点F3距离母线M的距离为45km。采样率为1MHz。对到达保护测量端M和N的三相电压和电流进行2ms的采样。

图3 仿真模型图

发生故障后,首先从故障波形中提取故障分量,进行相模变换后,计算出正反向行波,本文使用小波变换提取行波波头。

图4 模量提取过程
3.1 F1点发生金属性短路接地
F1点发生金属性短路接地相对于保护 M和保护N而言属于区内故障,保护M和保护N检测到的正反向行波分别为(横坐标单位为μs,纵坐标单位为A)

图5 保护M检测到的正反向行波

图6 保护N检测到的正反向行波
保护 M和保护 N区内故障正反向行波同时到达,因此对反向行波进行小波分解

图7 M端小波4层分解

表1 小波分解每一层模极大值
由表1可知,小波检测奇异性必须通过三层小波分解才能得到正确的结果。根据基于行波波头的行波差动保护算法进行分析。第三层M端和N端的模极大值分别为 Mm(F1) =-55.57,Mn(F 1)=- 55.44,到达时刻分别为248μs,198μs。线路的波形速度为2.98× 108m/s,所以线路MN波形时间为453.02μs,M端提取到的是反向特征值,所以将对端传来的模极大值延时453.02μs后与本端信息进行比较。延时后M端对应模极大值时刻为198+453=651μs,时间不在 Δt范围内不需要进行校正,对应 Mmj(F 1) =5.23
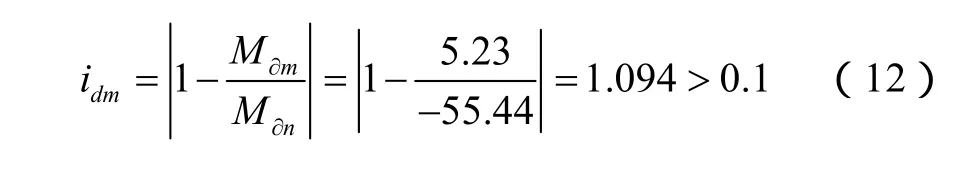
同理保护2的端对应 idn=1
M和N端的动作判据均大于门槛值0.1,保护动作。
3.2 F2点发生金属性短路接地
当F2点发生A相金属性短路接地时,对保护M而言为正方向区外故障,保护M和保护N检测到的正反向行波分别为(横坐标单位为μs,纵坐标单位为A):
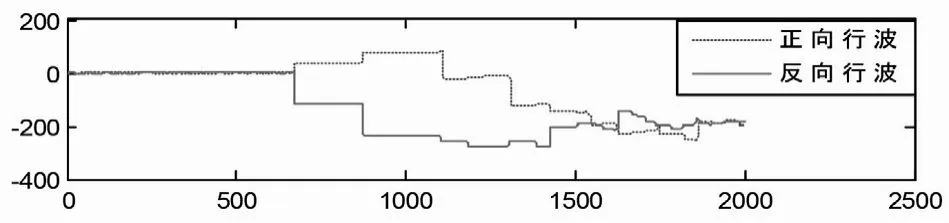
图9 保护M检测到的正反向行波
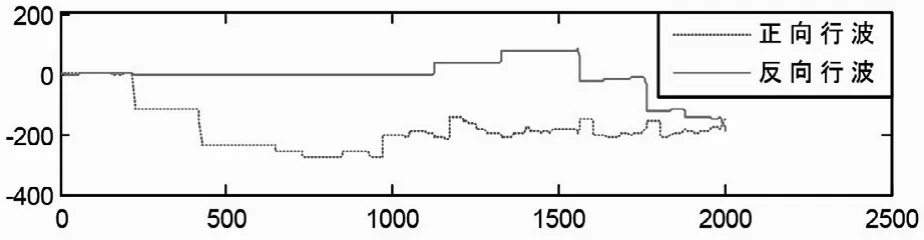
图10 保护N检测到的正反向行波
保护M正反向区外故障时,对保护M正反向行波同时到达,对保护N正向行波先于反向行波到达。因此保护M提取反向特征值,保护N提取正向特征值。经小波分解后如图11所示。
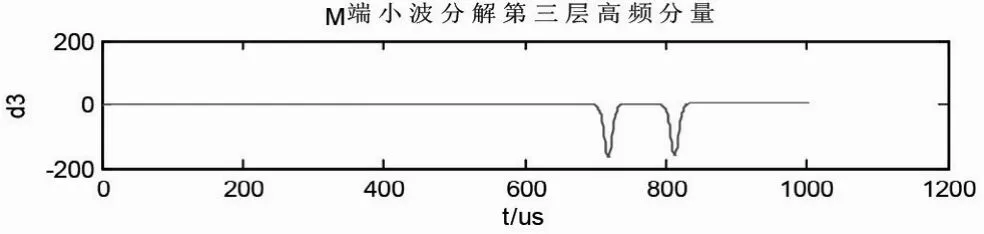
图11 M端小波分解第三层高频分量

图12 N端小波分解第三层高频分量
由信号处理结果得M端N端模极大值分别为,Mm(F2)=-226.7,Mn(F2)=-228。到达时刻分别为665μs,211μs。线路 MN 波形时间为 453.02μs,根据保护算法,将正向特征值延时453.02μs后与反向特征值进行比较。延时后M 端对应时刻211+453=663μs,时间差665-663=2μs在 Δt范围内进行校正,对应 Mmj(F 2) =-226.7

同时N端对应 idn=0.00573
两端的动作判据分别均小于门槛值0.1,判为区外故障,保护1和保护2均不动作。
3.3 F3点发生金属性短路接地
当F3点发生A相金属性短路接地时,对保护M而言为反方向区外故障,保护M和保护N检测到的正反向行波分别为(横坐标单位为μs,纵坐标单位为A):

图13 保护M检测到的正反向行波

图14 保护N检测到的正反向行波
保护M反方向区外发生故障时,对保护M正向行波先于反向行波到达,对保护N正反向行波同时到达。因此保护M提取正向向特征值,保护N提取反向特征值。经小波分解后如图15和图16所示。

图15 M端小波分解第三层高频分量
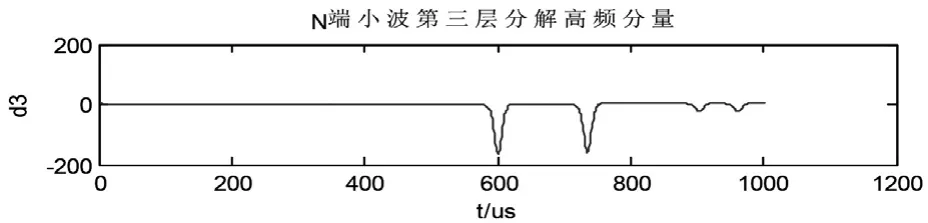
图16 N端小波分解第三层高频分量
由信号处理结果得 M端 N端模极大值分别为Mm(F3)=-164.3,Mn(F3)=-164.7。到达时刻分别为147μs,601μs。线路 MN 波形时间为 453.02μs,根据保护算法,将正向特征值延时453.02μs后与反向特征值进行比较。延时后N 端对应时刻147+453=600μs,时间差 601-600=1μs在Δt范围内进行校正,对应 Mn(F 3) =-1 64.7有

同时N端对应 idn=0.0037
两端的动作判据分别均小于门槛值0.1,保护均不动作。
4 结论
针对传统的行波差动保护速动性差和对传输通道要求高的问题,提出改进的差动保护方案,即在小波变换基础上的基于行波波头的行波差动保护方案,并在Matlab中对此算法在各种故障情况下进行仿真研究。仿真验证该方法的可行性。
[1]BERGLUND R O,MITTELSTADT W A, SHELTON M L,et a1.One·cycle fault interruption at 500kV:system benefits and breaker design[J].IEEE Transactions on Power Apparatus and System,1974,PAS-93(5):1240-1248.
[2]AKKE M,THORP J S.Algorithm for fast transmission line protection[J].IEEE Transactions on Power Delivery,1998,13(1):66-72.
[3]苏斌,董新洲,孙元章.基于小波变换的行波差动保护[J].电力系统自动化,2004,28(18):25-29.
[4]董杏丽,葛耀中,董新洲,等.基于小波变换的行波测距式距离保护原理的研究[J].电网技术,200l,25(7):9-13.
[5]董杏丽,葛耀中,董新洲.基于小波变换的无通道全线速动行波保护[J].电力系统自动化,2001,25(10):18-22.
[6]程正兴.小波分析算法与应用[M].西安:西安交通大学出版社,1998:4-19.
[7]SERRA J.Image analysis and mathematical morphology[M].London:Academic Press,1982:147-236.
[8]林湘宁,刘沛,刘世明,等.电力系统超高速保护的形态学一小波综合滤波算法[J].中国电机工程学报,2002,22(9):19-24.
[9]L90 Line Current Differental Relay.Privacy Policy I Terms and Condition@General Electric Company[M]1997-2001.

