UNIFAC模型结合Butler方程测算液体混合物表面张力

魏立岩

(河北衡水学院分院，河北 衡水 053000)

液体混合物表面张力数据是过程和理论研究所必需的基础数据，对于液体混合物表面张力测定、关联和推算已成为化工和理论研究的重要课题。而利用少量的已知实验数据对液体混合物表面张力进行推算就更具有重要的实际意义。其中利用基团贡献法进行推算的方法收到了良好的效果。本文在利用UNIFAC模型的基础上对分子结构进行重新拆分，利用拆分后的基团作用参数对体系的表面张力进行计算的方法。

1 理论部分

1.1 UNIFAC 模型

UNIFAC功能基团活度系数模型是 UNIQUAC(Universal Quassi-Chemical)模型基团化的结果。UNIQUAC模型是Abrams和Pranusniz在1975年根据液体胞腔理论、Guggenhein的似化学方程(quasi-chemical equation)并结合Wilson局部组成概念发展而成。它是基团贡献法的成就之一，它的基本思想是把混合物种组分的活度系数与组分之间的能量相互作用参数联系起来，当使用这些参数推算在远离临街条件下非电解质液体混合物的活度系数时，除系统温度和压力外仅需知道混合物中各组分的分子结构和必要的集团参数，并不需要有关联特定的混合物的实验数据。

1.2 Butler方程

大多数关于液体混合物表面张力的描述都是建立在将液体表面层看作是一个气液相之间的独立的体系的假设之上的，基于这一假设，结合经典热力学理论，可导出关于液体混合物表面张力的计算公式Bulter首先于1932年从热力学理论出发，导出液体混合物表面张力的理论公式：

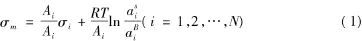
式中σm代表液体混合物表面张力，σi是纯组分i的表面张力，Ai和分别为组分的摩尔表面积，和分别是 组分表面相和体相中的活度，R为气体常数，T是体系的绝对温度，N为体系的组分数。为了使UNIFAC模型与Buttler方程相结合，实现UNIFAC基团贡献法对液体混合物表面张力的推算，本文利用两个基本假设：

式中Vi是纯组分 i的液体摩尔体积，N为 Avogadro常数(6.023 ×1023)。

从假设(1)可得到如下方程组：

2 计算过程

本文根据以上的理论和公式建立了求解方程组(3)的计算步骤如下：对含有N个组分的液体混合物，在给定体系温度T和体相摩尔分数时，可由UNIFAC模型和方程(2)计算和

3 结果与讨论

计算结果显示采用本文方法对液液体系的表面张力的推算改进不明显。误差原因：

1)偏摩尔表面积;2)数据来源 使用的是通过气液数据进行回归参数，如果采用写体混合物表面张力的实验数据进行回归效果会好;3)计算的体系较少。

[1]赵传钧.基团贡献法—物理化学在化学和化工上的一种应用.化学通报，1983(10)

[2]罗长青.UNIFAC功能团法推算气—液平衡及其计算机应用.化工设计通讯，1987，13(4)

[3]Prediction of surface tensions of nonelectrolyte solutions.Chemical Engeneering Science，Vol.44，No.3，pp.782-786，1989