扰动算子的群可逆性及其表示
胡春梅
(丽江师范高等专科学校 数计系,云南 丽江 674100)
1 引言与引理
设X和Y为两个任意可分的Banach空间,L(Χ,Υ)是从X到Y的有界线性算子的全体,L(Χ,X)记为L(Χ)。对任一算子A∈L(Χ,Υ),R(A),N(A)和Reσ(A) >0分别表示A的值域,零空间和特征值的实部。
定义1[1]设 A∈ L(Χ),称满足下列方程的算子 X∈L(Χ)
(1)AXA=A,(2)XAX=X,(3)AX=XA为A的群逆,记X=Ag。且A的指标为1,即Ind(A)=1。
引理1[2]设A∈L(Χ)且Ind(A)=1,则在空间分解Χ=R(A)⊕R(A)⊥下,存在可逆算子
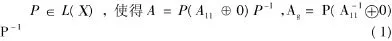
此时,

引理2 设A∈L(Χ)且Ind(A)=1,E∈ L(Χ)。若‖AgE‖<1,则I+AgE和I+EAg均可逆,且
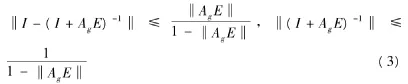
2 主要结果
定理1 设A∈L(Χ)且Ind(A)=1,E∈L(Χ),B=A+E,‖AgE‖<1,AAgEAπ=0,
若EAπ=0,AπE=0则 B是群可逆的且 Bg=(I+
证明:由引理1可知,在空间分解Χ=R(A)⊕R(A)⊥下,A、Ag和AAg、Aπ分别具有(1)和(2)中的形式,且可设E=
由条件AAgEAπ=0,EAπ=0,AπE=0,可计算出E12=0,E21=0,E22=0.
又因为‖AgE‖ <1,则由引理2,I+AgE可逆,即I+Ag可逆,则A11+E11可逆,所以由引理1知B是群可逆的。

[1]DJORDJEVIC D.S.,VLADIMIRI RAKOCEVIC。Lectures on generalized inverse[M].Faculty of Sciences and Mathematics:University of NiS,2008.
[2]Conway J.B.A Course in Functional Analysis.Springer-Verlag,New York Inc.1990.
[3]BEN-ISRAEL A,GREVILLE T.Generalized Inverse:Theory and Applications[M].New York:Wiley,1974.
[4]Castro N,Koliha J J,Wei Yi Min.Integral representation of Drazin inverse AD[J].Electronical J.Linear Algebra,2002(9).
[5]杨凯凡,杜鸿科。扰动算子的Drazin可逆性及其Drazin逆的表示[J]。数学学报,2010,53(6)。

