淹没水跃Fr数对消能率影响数值模拟研究

潘忠良,马建东

(1.嘉兴市水利水电勘察设计研究院,浙江 嘉兴 314001;2.海盐县秦山街道农技水利服务中心,浙江 海盐 314303)

1 问题的提出

淹没水跃常见于平原地区的水利工程中的消能设施中,本文选取文献[1]的3组淹没水跃进行研究,试验装置见图1。该试验的实测数据采用激光多普勒量测技术(LDA)进行采集,实测成果已多次被数值模拟方法验证[2-4],但发表的相关文献对水跃的内部水流结构和宏观特性,特别是消能率的分析还不够深入,本文选择合适的紊流模型和数值模拟方法用于3组不同进口Fr数水跃的流态分析,并就水跃的消能率的数值计算方法进行研究。

2 数值模型的建立

2.1 数值模拟条件

因试验是在一水平底等宽矩形水槽内完成,几何边界相对简单,可忽略侧边界对水跃的影响,因此只对其进行二维立面数值模拟,试验装置见图1,计算参数见图2,数值模拟条件见表1。

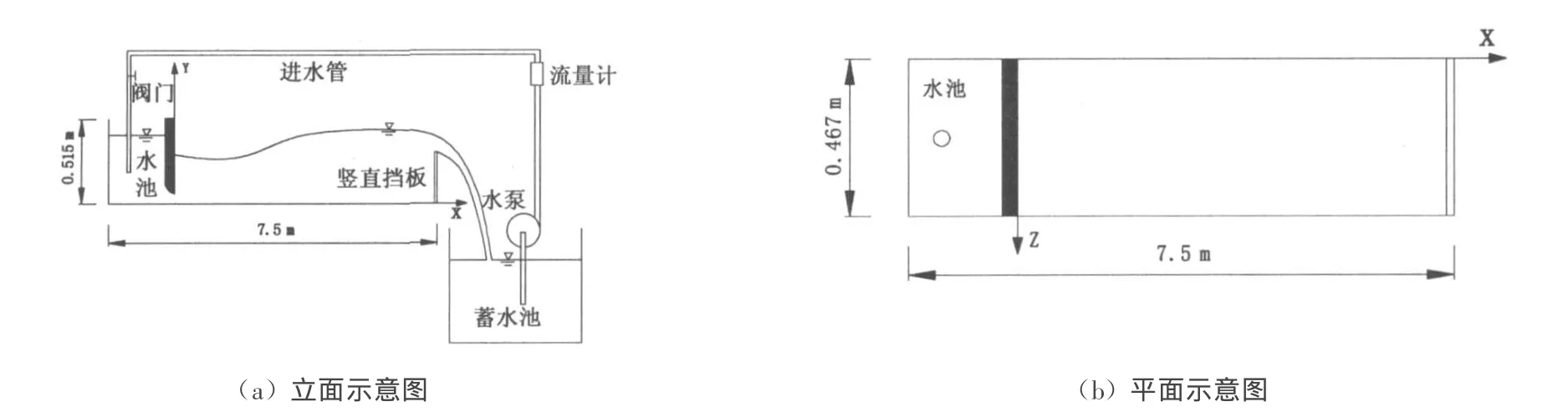
图1 文献[1]试验装置图

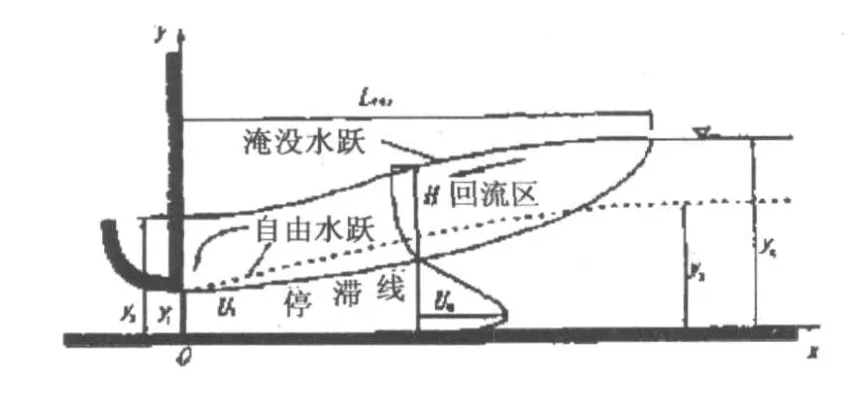
图2 淹没水跃计算参数示意图

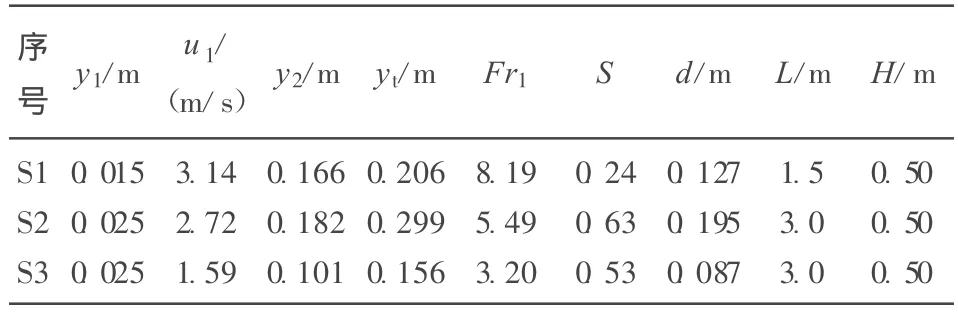
表1 水跃数值模拟条件表

表中:y1为进口水深(m);u1为进口断面平均流速(m/s);y2与 y1对应的自由水跃共轭水深(m),按 y2=计算;y为下游水深(m);Fr为进口佛汝德数,按计算;S为淹没度,文献[1]定义S=为计算域尾部挡板高(m),这是为了保持下游水深不变而设的,其近似值按巴赞公式[5]试算得到;L为计算长度(m);H为计算域高度(m),包括水相和气相2相高度之和,为防止水流溢出,气相高度近似按初始水深的1倍取值,H均取0.5 m。

2.2 定解条件

2.2.1 边界条件

水流入口为速度进口(Velocity-inlet),顶边界为压力进口(Pressure-inlet),出口为压力出口(Pressure-outlet),其余均为无滑移固壁边界(Wall)。固壁边界条件中壁函数不考虑壁面粗糙度影响,视为光滑固壁;对于近壁面处采用标准壁面函数方法来处理。工作压力约10.13 kPa,相对压力为0 kPa,参考位置选在出口顶端。计算区域及具体边界条件位置见图3。

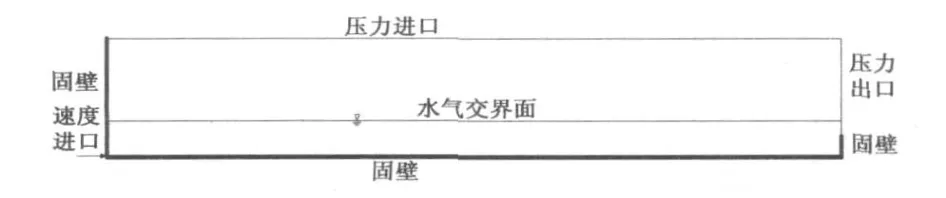
图3 计算区域及边界条件设置图

2.2.2 初始条件

本章的算例对入口、压力入口及压力出口的紊动能 k和耗散率ε的初始值均按实测得出的经验公式计算[6]:

式中:u1为进口处断面平均流速(m/s);y1为进口处水深(m)。

2.2.3 数值计算方法

网格均为基于梯度自适应进行局部加密后的网格,以CFD软件FLUENT6.3为计算平台,用Realizable k-ε紊流模型封闭方程、标准壁函数简化处理近壁流动、自由液面的变化用VOF法、速度和压力间的耦合用PISO法,压力离散用体力权重(Body Force Weighted)法,显示几何重构格式用于VOF方程离散,对动量方程、K方程和ε方程均采用一阶迎风格式离散求解,控制方程及FLUENT求解步骤参见文献[6]。

3 数值模拟分析

3.1 流态分析

淹没水跃的流态可分为外在和内在2方面。外在方面表现在自由液面的的变化(见图4),计算开始后,进口后水位快速下降,随后又缓慢回升,小幅振荡最终平稳,而且可发现表面波的产生及传播并无反射地通过计算区域的情形;内在方面则表现为流线的变化,图5为淹没水跃由静止到基本稳定的系列流线图,由图5可看出,随着时间的推进,水跃段内有漩滚的生成及破裂的现象。由S1出口的质量流量监测曲线可知,计算至2 000步 (即10 s)时,流动基本稳定,水深变化很小,此时水跃的位置也已稳定,因此可以判断流态基本稳定。S2和S3情况下的流态与之相似,不再表述。

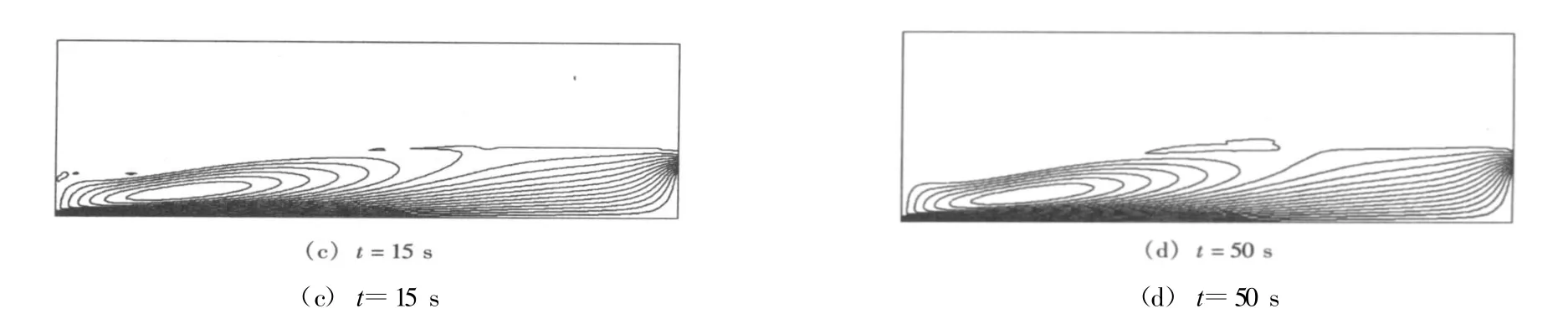
图5 S1情况下流线变化图

3.2 实际消能率计算及分析

本小节将给出经典淹没式水跃的实际消能率的数值计算方法操作步骤,并就实际消能率与名义消能率的差异进行分析。

消能率一般表达式[7]:

式中:E1、E2分别为消能设施进口前和出口后单位水体的时均能量(m)分别为断面渠底高程(m)、断面平均流速(m/s)、断面渠底的时均压力(m)及时均断面水深(m)。

为与式(3)相区别,定义水跃实际消能率η′的计算公式为:

E1′分别表示进口断面和跃后断面的紊动能水头(m),计算公式为:

式中:K为断面平均紊动能,紊动能与质量流量有关,其计算公式:

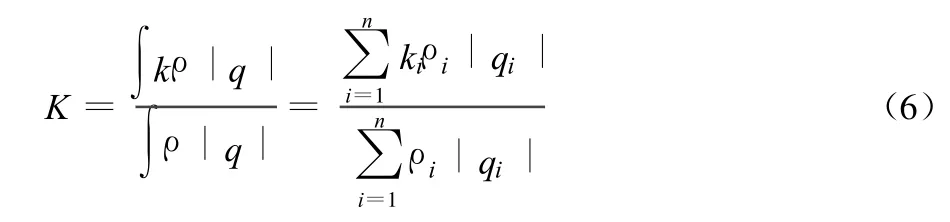
图6、7分别为紊动能k和紊动能耗散率ε的分布,从图中可明显看出紊流剪切层的存在,且沿剪切层和底壁的紊动能及其耗散率的等值线非常密集。k和ε的分布形状类似,均反映出主流与表面漩滚的交界处,紊动最为剧烈,其中ε的分布较k的分布稀疏,表明漩滚具有较高的紊动能,而紊动能的耗散则更多地集中在主流与漩滚的交界处。由于缺乏这方面的实测资料,因此无法进行进一步的定量比较,但能给出紊流特征量,也可充分体现紊流数学模型在水跃计算中的突出优点,为深入分析水跃内部的紊流结构,提供有效手段。

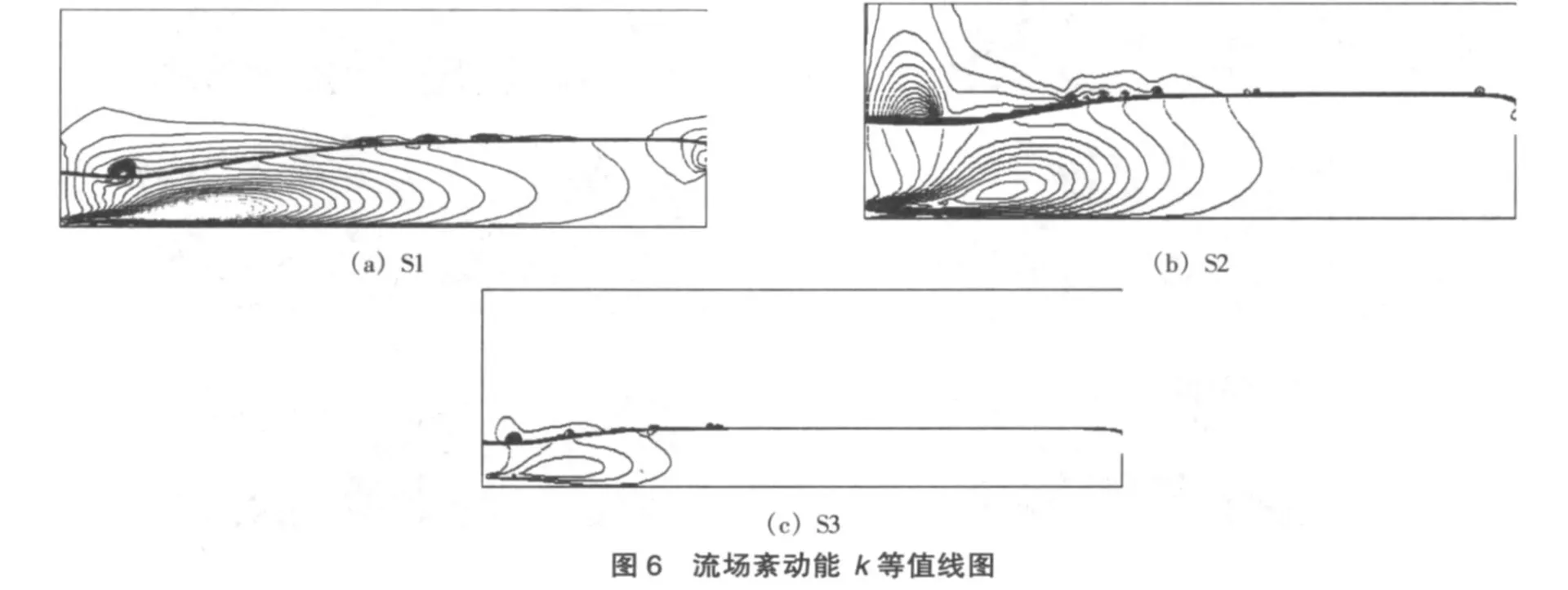
图7 流场紊动能耗散率等值线图

表2是基于FLUENT6.3计算得出3种不同进口Fr数和淹没度下的名义消能率和实际消能率。

表2 消能率计算表

表中为工程中初估的消能率计算公式:

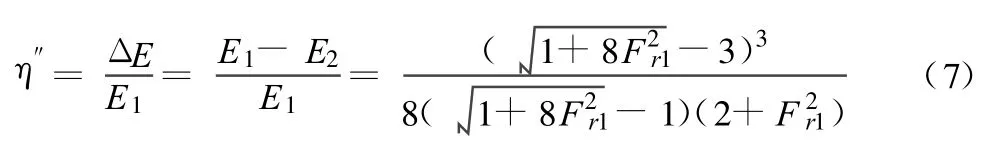
由表2可知,S1的名义消能率和实际消能率均与此经验公式的值非常接近,而对于S2和S3却相差较多,这主要因为公式(7)没有考虑跃后水流大尺度紊动的能量[8]。由表2可看出S3对应的水跃消能率最低,S2次之,S1最高。在实际消能率和名义消能率相对误差上,高Fr1数S1的值最小,仅为0.9%,低Fr1数S3最大,达到了41.2%。而且从表中可知S3的实际消能率仅为3.8%,说明水跃段紊动能消耗差,跃后紊动能很大,从图中的S3紊动能耗散率分布也可以看出,S3紊动能耗散率几乎为零,因此消能效果最差。综上所述,在对低Fr数高淹没度的水跃进行消能率计算时不可忽略跃后紊动能的影响,否则所得消能率偏大。

4 结 语

(1)通过对淹没水跃实际消能率的深入研究发现,低Fr数淹没水跃的实际消能率与名义消能率差距较大,而且经验公式计算的消能率值偏大,低Fr数水跃常见于平原地区的水利工程中,因此在设计消能设施时应引起足够的重视;

(2)由于本文着重对实际消能率计算方法进行探讨,而具体的计算对象只有3种情况,进口Fr数和淹没度的取值比较有限,因此对相同Fr数、不同淹没度以及相同淹没度、不同Fr数情况下的各种水跃中跃后紊动能对实际消能率的影响还有待研究。

[1]Long D,Stefller P M,Rajaratnam N.LDA study of flow structure in submerged hydraulic jumps[J].Hydraulic Research,IAHR,1990,28(4):437-460.

[2]戴会超,王玲玲.淹没水跃的数值模拟 [J],水科学进展,2004,15(3):184-188.

[3]刘清朝,陈椿庭.水跃紊流特性的数值研究 [J].水利学报,1993(1):1-10.

[4]杨建明,吴建华.淹没水跃的数值模拟 [J].水动力学研究与进展:A辑,2001,16(4):405-411.

[5]毛根海.应用流体力学 [M].北京:高等教育出版社,2008.

[7]潘忠良.某水闸消力池自由液面数值模拟的研究[J].浙江水利科技,2008(6):25-27.

[8]吴持恭.水力学 [M].4版.北京:高等教育出版社,2008.

[9]张声鸣.低佛氏数水跃消能中的几个问题 [J].人民长江,1992,23(7):39-45.