支持向量机在水库大坝变形中的预测分析

郝长春

（安徽省水利水电勘测设计院，安徽 蚌埠233000）

为了有效保障水库大坝的安全运行和掌握大坝的运行状态，目前大多使用自动化和智能化程度较高的测量机器人对大坝进行实时连续的精密观测。测量机器人测角精度达±0.5″，测边精度达±（1mm＋1ppm×D）［1］，为后续大坝的变形分析提供了高精度的三维坐标。

大坝在运行过程中受到的影响因素主要有水位、温度、时效及日照等，这些因素具有很强的模糊性、离散性、随机性等特点［2］，而且各种影响因素之间的关系多为非线性的，很难用一种确定的模型实时逼真地反映大坝的变形状态。目前，用于大坝变形分析的方法主要有BP神经网络模型、统计回归模型等智能算法［3］，而本文探索使用SVM支持向量机技术建立实时分析大坝变形的预测模型。通过对相同的变形监测数据进行对比分析发现SVM支持向量机模型比BP神经网络模型、线性回归模型等在解决非线性、高维空间、小样本及局部极小值等方面有更多的优势。

1 支持向量机理论

1.1 统计学习的VC维理论和支持向量机

早期多采用经验风险最小化理论，即ERM准则来解决模型的逼近问题，但由于ERM准则是根据经验直观的、想当然的做法，所以缺乏必要的理论基础。VC维理论是统计学习理论用来衡量函数集性能的重要指标，在某种程度上能反映函数集的学习能力，对学习机器泛化性能有直接的影响，如VC维越大，则学习机器的容量就越大，其本身的结构就越复杂。

机器学习想要达到的真正目的是使经验风险和VC维都尽可能的小，以取得较小的真实风险，即对后期的输入数据有更好的推广性［4］。下面用经验风险与真实风险之间的关系解释这种推广性。

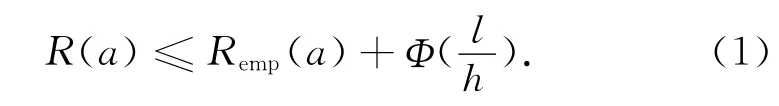
式中：R（a）为真实风险；Remp（a）为经验风险；l表示输入的样本数；h表示函数集的VC维；）被称作置信范围。如果能使经验风险和置信范围同时达到最小，那么实际风险也将能实现最小化的目的。

SVM是以统计学习理论为基础采用结构风险最小 化 （Structural Risk Minimization，SRM）理论［5］建立的，其基本思想是通过内积函数定义的非线性变换将输入空间映射到一个高维的特征空间，并且在高维的特征空间中寻找输入变量和输出变量之间的一种非线性关系（最优分类面）。可设输入样本为xi（i＝1，2，…，k），对应的输出为yi∈（＋1，－1），方程x·w＋b＝0为高维空间中的最优分类面，其中：w，b表示方程的系数，且满足下面的约束条件

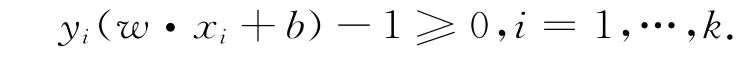
设x到最优分类面的距离为

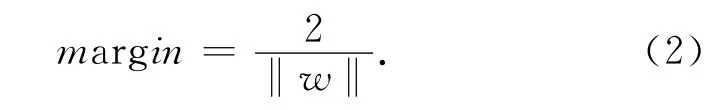
在高维空间使间隔margin的值达到最大且满足下面等式的样本点就是支持向量（Support Vector，VC）［6］

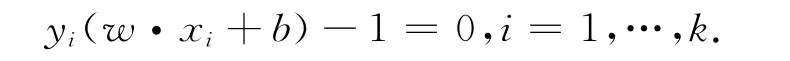
在函数拟合问题中，通常运用核函数将大量离散的非线性数据转化为高维空间中的线性问题。根据相关文献研究发现高斯径向基核函数更适合于非线性模型的建立，故本文选高斯径向基作为核函数

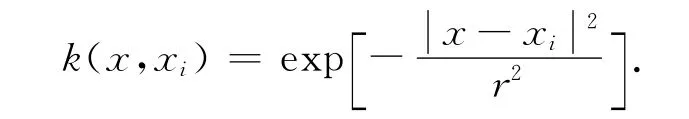
除此之外，常见的核函数还有d次多项式核函数、双曲正切核函数等。

1.2 支持向量机预测模型

设（x1，y1），（x2，y2），…，（xi，yi），xi∈RN，yi∈R，xi为输入向量，yi为输出向量，l为样本个数，Φ表示非线性映射，F表示通过映射得到的高维空间，则

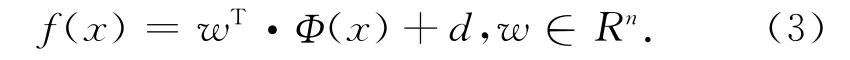
式中：w表示最优分类面的权值向量；d表示偏置量。引入下面的结构风险函数

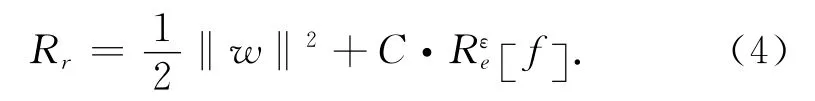
式中：‖w‖表示函数f（x）的复杂程度；C为惩罚因子；ε表示不敏感损失函数，其有如下的形式：

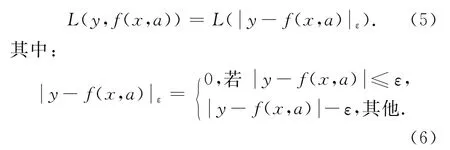
若实际值与预测值之间的差值不大于ε时，即认为预测值不存在损失；当它们之间的差值为“其他”情况时，也不惩罚那些造成偏差大于ε的样本值，这样可以使训练模型具有很好的鲁棒性。

支持向量的回归问题实质上是在一定约束条件下解下面的优化问题。

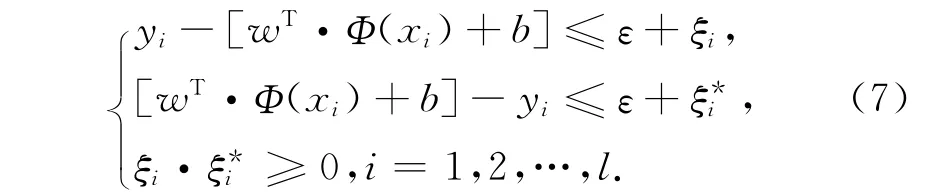
式中：ξ，ξ＊为松弛因子，表示在｜yi－［wT·Φ（xi）＋d］｜＜ε条件下训练误差的上限和下限。

需优化的问题为［7］

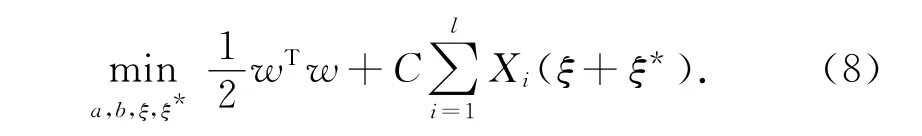
引入Lagrange函数求解上述条件下的优化问题，可以使式（9）成立。

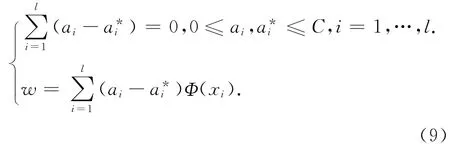
最终，应用式（4）中的对偶问题解非线性的回归问题：

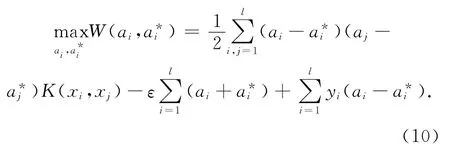
式中：K（xi，xj）＝Φ（xi）T·Φ（xj）表示用来描述高维空间的核函数，由式（3）、Lagrange函数及解得的ai和的值可得到回归函数［8］

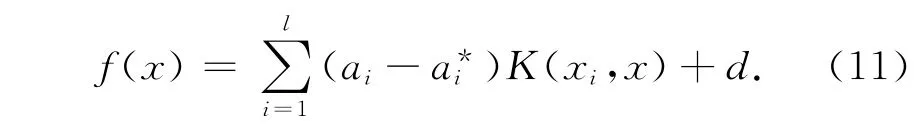
由式（7）可以发现，若输入向量xi不在｜yi－［wT·Φ（xi）＋b］｜≤ε的范围内，则将存在误差，这时可采用最小化目标函数的方法进行回归，避免了数据过拟合的问题。通过使用核函数进行低维到高维空间的转换，大大降低了运算的复杂度，摆脱了高维空间中维数的困扰，避免了“位数灾难”的出现。

2 基于SVM的大坝变形预测拟合模型

2.1 实例分析

皖东南某水库大坝为混凝土面板堆石坝，坝长252m，最大坝高为68m。整个监测网包括7个基准点和17个工作基点，如图1所示。采用TCA2003智能监测系统对大坝进行长期不间断监测。

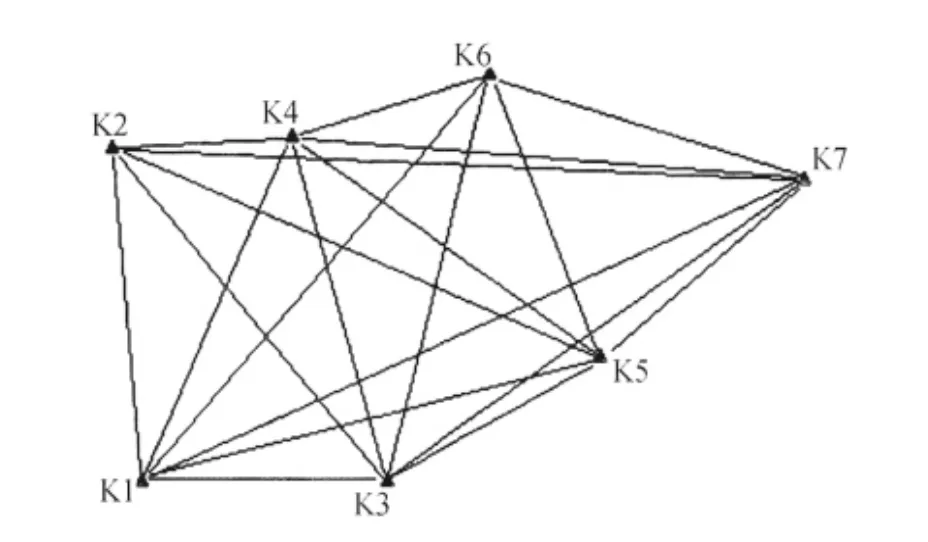
图1 监测控制网

为方便监测数据的处理，本文假设沿坝体的方向为X轴，与坝体垂直向下游的方向为Y轴正方向。本文选取位于大坝中间的工作基点BX7的101组数据作为一个实验样本，并且把前81组数据作为模型的学习样本，把剩下的20组数据作为预测样本。BX7点Y方向的位移和沉降及水位的数据分布分别如图2、图3、图4所示。

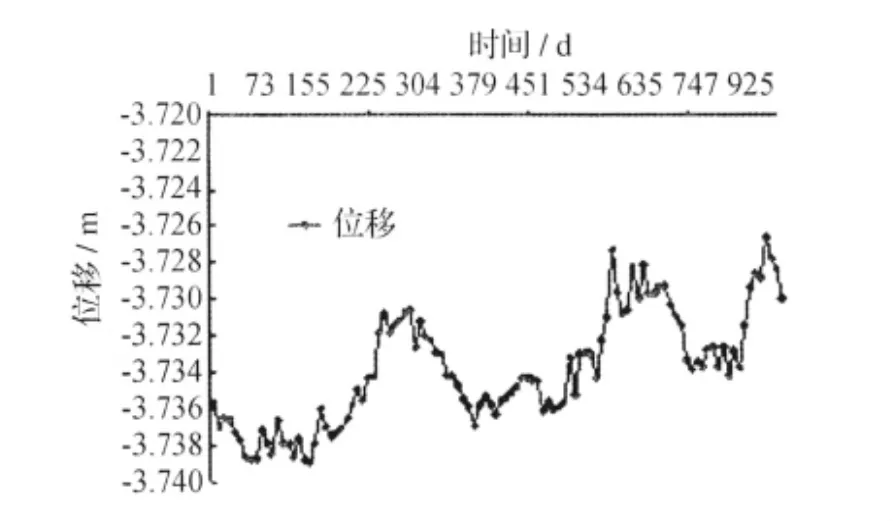
图2 BX7点Y方向位移分布

2.2 监测数据的预处理

本文采用“3σ准则”对数据进行粗差探测，假设｛x1，x2，…，xn｝为一观测值序列，采用一级差分的方法求每个观测值的预测值

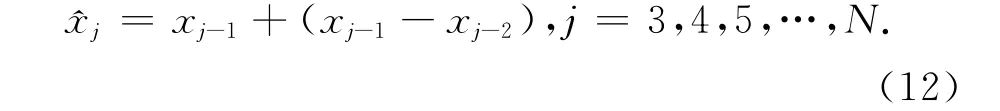
则实际观测值与预测值之差为

假设通过大量观测资料求得的观测值中误差为m，由式（12）和式（13）可得dj的均方差＾σd＝2m。当｜dj｜＞3＾σd时，则判定xj为粗差（奇异值），应将其剔除。

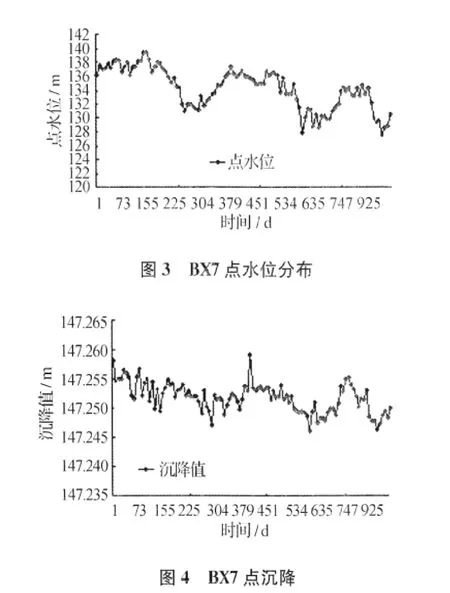
在BX7号点的沉降值分布图中存在急剧跳跃的数据，因而采用“3σ准则”进行探测，发现第54组数据的沉降值有异常，故将其剔除。为了保证数据的连续性和完整性采用下面的“线性内插法”对该组数据内插，内插值为147.253 2。

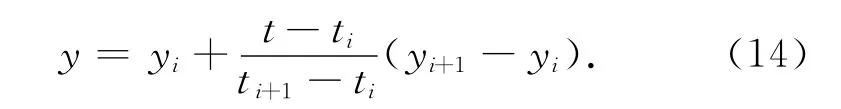
式中：y，yi，yi＋1为效应量；t，ti，ti＋1为时间变量。

2.3 SVM模型建立与预测

SVM、BP神经网络、多项式回归模型均采用相同学习样本和预测样本对BX7号点监测数据进行建模和预测，并对最终的预测精度进行对比分析。

鉴于大坝所受的主要影响因素，本文选取T（观测时的气温或者当天平均气温）、H（库水位），t1，t2，t3（时间t的函数）为观测量。

时间t的函数表达式为

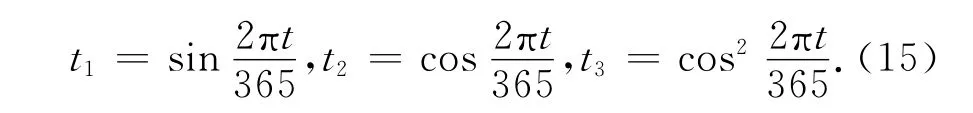
则大坝变形预测模型可以定义为

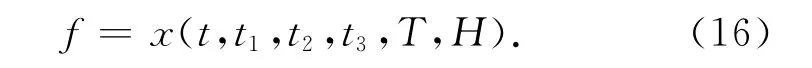
由学习样本值得基于SVM的大坝变形模型为

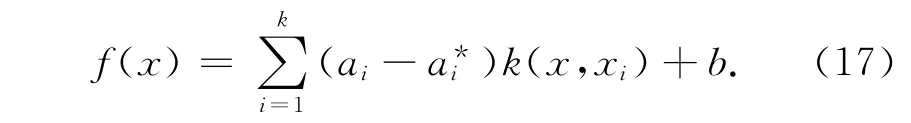
式中：x为待预测值的影响因子矩阵；xi为第i次观测的影响因子矩阵；k（x，xi）为径向基核函数、ai，b可通过求解二次优化问题得到。

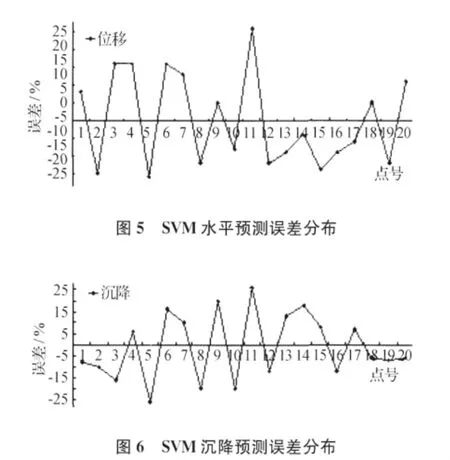
本文采用径向基核函数和交叉验证法建立拟合模型，通过对设置的样本进行学习，得出核参数γ为0.071 437，惩罚因子C为147.298 15，损失函数ε为0.029 173。采用解算的参数对预测样本进行预测，水平位移与沉降量的预测值与实测之间的误差分布如图5、图6所示。

2.4 其他模型的预测

2.4.1 BP神经网络模型的预测

本文建立了以特征向量T，H，t1，t2，t3为输入层，以监测值的变形量为输出层、一个隐含层的三层神经网络预测模型，对BX7号点的沉降监测值进行预测，预测误差曲线如图7所示。

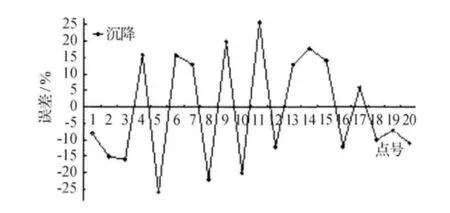
图7 BP神经网络沉降预测误差分布

2.4.2 多项式模型的预测

同样以水位、气温和时间为自变量，定义的多项式模型为

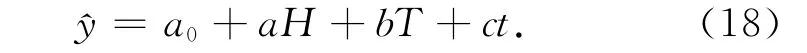
采用与前两种模型相同的学习样本，通过回归计算得a0＝－51.2、a＝0.003，b＝0.335，c＝0.052，则预测方程为

＾y＝－51.2－0.003 H＋0.335T＋0.052t.

通过对预测样本沉降量进行预测得到如图8所示的误差分布曲线。

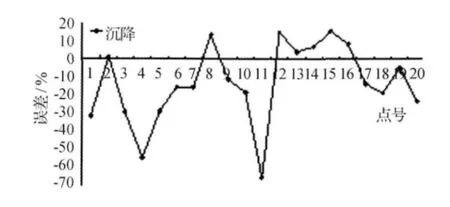
图8 多项式沉降预测误差分布

从以上3种模型对沉降量的预测误差曲线可以看出，SVM模型和BP神经网络模型具有相近的预测效果，两者分别有85%和75%的预测点落在±20%的范围内，而多项式仅有50%的点落在该范围内，并且SVM还具有很强的“鲁棒性”。

3 模型预测精度评定

本文选择平均绝对百分比误差（MAPE）、均方误差（MSE）、平均绝对误差（MAE）评定模型的预测效果，并进行对比分析，基本公式为

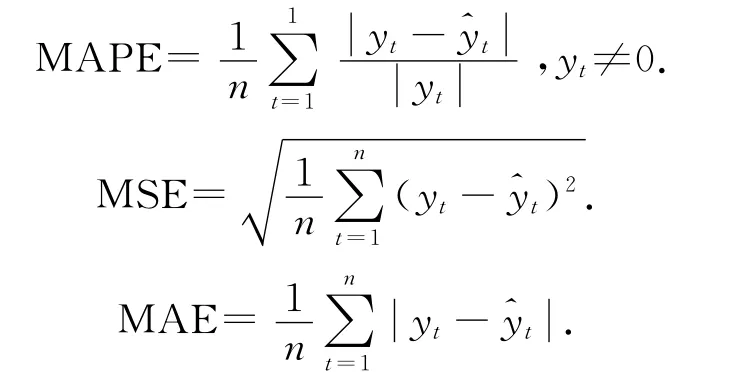
在上述的3种评定方法中，yt表示实测值；＾yt表示预测值；n表示预测值的个数，评定结果如表1所示。

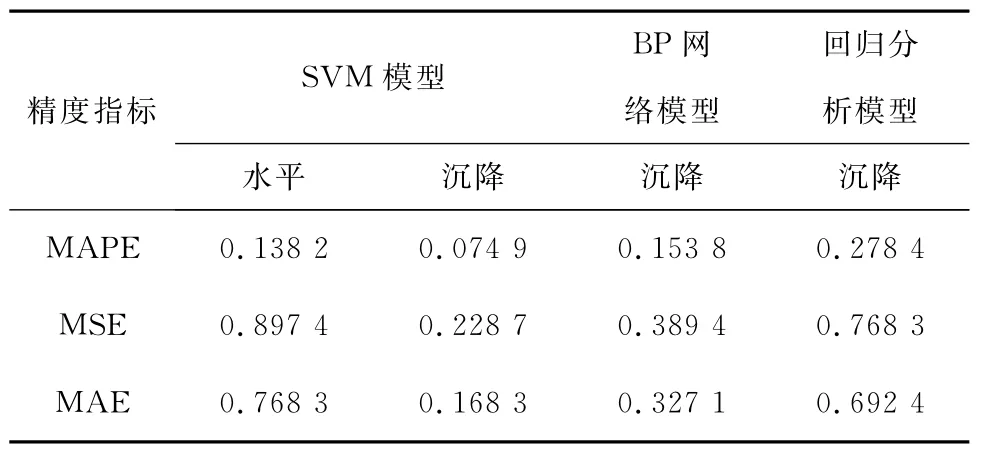
表1 3种预测模型的预测精度比较

由表1可知，在3个指标中SVM模型的沉降值最小，因而SVM模型在大坝预测上比BP网络模型和回归分析模型都有更好的效果。适合处理小样本、非线性的数据，建立的模型具有良好的推广性，采用核函数的方法巧妙地避免了数据处理时的“维数灾难”和局部多极值的问题。

4 结束语

通过模型的建立和预测分析可以发现SVM模型能够很好地表达复杂因素间的非线性关系。选择径向基核函数能够满足非线性监测数据由低维到高维的映射要求，避免模型的过度拟合，使建立的模型具有更好的泛化能力。而神经网络法是一种事后处理方法，并且存在过学习、收敛速度慢、易陷于局部极值等问题。从误差曲线图中也可以看出，中间有部分预测精度非常高，而后半部分预测精度较低，因而SVM模型更适合于大坝变形数据的预测。

［1］喻兴旺.TCA2003全站仪在港口湾水库大坝变形监测中的应用［J］.水电自动化与大坝监测，2003，27（5）：48－50.

［2］张真真.支持向量机在大坝安全监测资料分析中的应用［D］.西安：西安理工大学，2008.

［3］岳建平 田林亚.变形监测技术与应用［M］.北京：国防工业出版社，2007.

［4］李国正，王猛，曾华军.支持向量机导论［M］.北京：电子工业出版社，2005.

［5］Vapnik，V.The Nature of Statistical Learning Theory［M］.New York：Springer－Verlag，1995.

［6］Druker，H.Butges，C J.Kaufman，L C.Smola，A.Vapnik，V.Support vector regression machines［J］.Advances in Neural Information Processing Systems，1997，9：155－161.

［7］Christopher J.C.Burges.A Tutorial on Support Vector Machines for Pattern Recognition［J］.Journal of Changde Teachers University，1998.

［8］张学工.关于统计学习理论与支持向量机［J］.自动化学报，2000，26（1）.

［9］张宏伟 康世英.变形观测数据处理粗差的定位与剔除［J］.桂林工学院学报，2003，23（3）：310－313.