初弯曲和残余应力对焊接工字钢梁模态影响的数值模拟

瞿丽华，韦芳芳，黄建红，赵海波

(1.河海大学 土木与交通学院，江苏南京 210098；2.南京水利科学研究院，江苏 南京210029)

0 前 言

焊接工字钢梁是由三块钢板焊接而成，尺寸多样，制作方便，造价低廉，它是在钢结构设计中运用最广泛的结构形式。随着钢结构高速发展，问题也不断显现，国内外都发生过不同类型，不同程度的建筑钢结构的工程事故。比如辽宁省营口市经济技术开发区营口港在建锅炉房施工过程中发生钢屋架倒塌事故；俄罗斯首都莫斯科鲍曼市场顶部坍塌；法国戴高乐机场候机厅坍塌事故等，这些事故都造成了重大人员伤亡。造成这些事故的原因很多，建筑结构的健康检测能从源头上界定承载力不足和不安全的结构，并尽早进行加固，可以大大减小事故的发生率[1]。而动力特性的检测则是结构健康检测的重要内容，同时，梁作为建筑物的主要承重构件，若梁的固有频率与周围的激励频率近似将对结构造成巨大影响，所以这也给研究梁的动力特性提供了充分条件。钢梁在焊接过程中产生的残余应力及在运输安装过程中产生的初弯曲等初始缺陷会对结构的动力特性会造成一定的影响，已有研究采用理论推导，试验研究或者在数值模拟的方法来考虑初弯曲和残余应力对构件动力特性的影响。比如中国农业大学的高永毅等通过理论推导得出了残余应力对薄板构件固有频率的影响[2]；李文威等通过试验研究得出了铸铁构件固有频率与其残余应力关系[3]；孙强等人也通过理论推导得出了初弯曲对杆件动力性能的影响[4]。目前，残余应力和初弯曲等初始缺陷对钢结构构件影响的深入研究大多是针对其承载能力以及稳定性[5]，而针对结合健康检测的工字钢梁的模态分析还不全面，而且占大多数的理论推导和试验研究非常费时，少数采用有限元分析残余应力的方法是在构件划分的单元上逐个施加初应力，过程繁琐。所以本文基于上述研究现状，利用有限元软件ANSYS分别采用施加等效横向荷载，改变局部弹模的方法模拟两端固定的工字形截面钢梁分别在初弯曲和残余应力两种初始缺陷影响下的振动，比较了前四阶振型得出初始缺陷对工字钢梁模态即动力特性的影响。

1 初弯曲及残余应力对焊接工字钢梁的模态影响分析

1.1 有限元模型

本文通过ANSYS建立焊接工字钢梁的有限元模型。采用Solid45单元进行模拟，钢材的初始弹性模量取 E=2.06×1011Pa，密度为 ρ=7 850 kg/m3，泊松比为ν=0.3，模型跨度为L=10 m，截面尺寸为:翼缘 b×t1=0.125 m×0.010 m，腹板 h×t2=0.400 m×0.008 m，约束条件为两端固结，有限元模型及截面尺寸如图1，图2所示。

图1 焊接工字钢梁有限元模型

图2 焊接工字钢梁截面尺寸

本模型采用ANSYS模态分析中默认分块兰索斯法即可[8]。

有限元模型在没有考虑初弯曲或残余应力时的前四阶振型如图3所示。

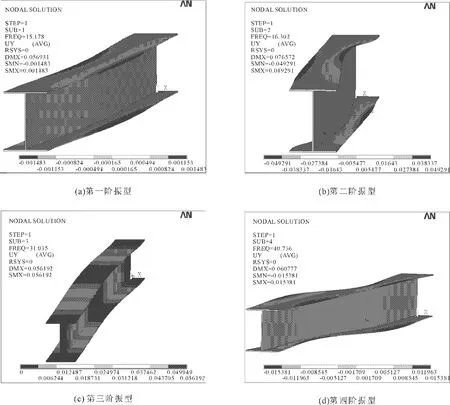
图3 工字钢梁无初始缺陷时的前四阶振型

从图3可以看出，构件无初始缺陷时，第一阶振型，工字钢梁翼缘与腹板均在xz平面内向x轴正方向弯曲，构件z轴方向中心位置的振幅最大。第二阶振型，工字钢梁整体绕腹板中心逆时针扭转。上翼缘在xz平面内向x轴负方向弯曲，下翼缘在xz平面内向x轴正方向弯曲。第三阶振型，构件整体只在yz平面内向y轴正方向弯曲，梁中部的竖向位移最大。第四阶振型，整体在xz平面内发生二阶弯曲，方向为逆时针，上下翼缘在xz平面内x，z两个方向上都发生翘曲，且绕腹板中心线呈轴对称变形。

1.2 初弯曲对模型模态的影响

为了考虑初弯曲对焊接工字钢模态参数的影响，将《钢结构规范》中的受弯构件在担任主梁时挠度容许值 ω=L/400作为初弯曲值[9]。由于初弯曲是构件在运输安装过程中产生的初始挠度，所以初弯曲的影响可用一个横向荷载产生相当挠度的影响来代替[4]。先在模型上施加单位荷载得出挠曲值，换算出当挠曲为初弯曲值时的荷载大小，再进行模态分析，得到的振型如图4所示。

图4 工字钢梁考虑初弯曲时的前四阶振型

从图4中可以看出，在构件上施加初弯曲后，相比于图3，第一阶振型，工字钢梁除了整体在xz面上向x轴正方向发生弯曲外，同时在yz面上向y轴负方向发生弯曲，且下翼缘在xz平面内的弯曲程度大于上翼缘。第二阶振型，构件整体的扭转变为顺时针，扭转中心从腹板中心移至靠近下翼缘处。另外，上翼缘在xz平面内向x轴正方向也发生了弯曲，下翼缘在xz平面内向x轴负方向也发生弯曲，且上翼缘的弯曲程度大于下翼缘，腹板没有明显弯曲。第三阶振型，整体也只在yz平面内发生弯曲，且振型形式也一致。第四阶振型，整体也在 xz平面内发生二阶弯曲，但是上翼缘同时在xz平面内的两个方向上顺时针扭转，而下翼缘在xz平面内x，z两个方向上均发生逆时针扭转。

在一般结构的健康检测中，通过应变模态变化率可以精确地判断构件损伤位置[10]，所以本文列出了完善模型与考虑初弯曲影响的工字钢梁的振动频率及变化率，如表1所示。

从表1可以看出，考虑初弯曲时，各阶频率与未考虑初始缺陷时的基本一致，但结合图4来看，第四阶振型还出现轻微扭转。总之，考虑初弯曲对焊接工字钢梁来说有一定的影响，但影响均在1%范围内，可以忽略不计。

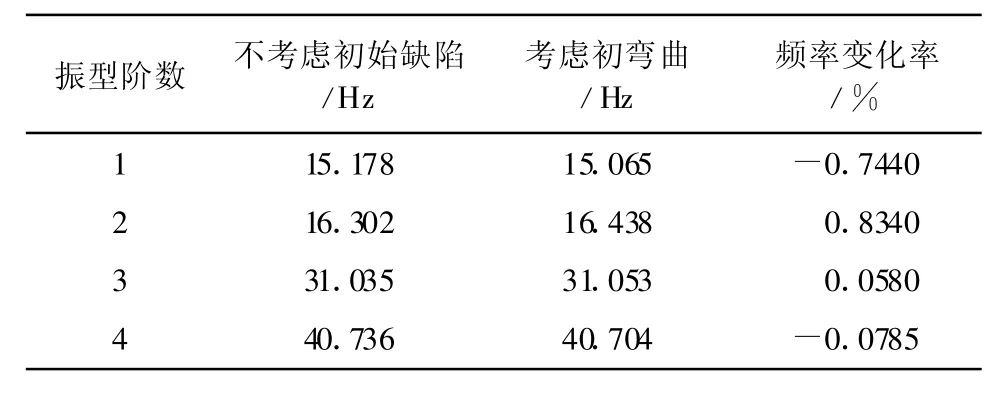
表1 考虑初弯曲影响的工字钢梁前四阶频率对比

1.3 残余应力对模型模态的影响

残余应力在构件还未承受荷载之前就已存在，是构件中自相平衡的初始应力。产生残余应力的主要原因是钢材热轧、火焰切割、焊接、校正等加工制造过程中不均匀的高温加热和不均匀的冷却。残余应力的分布和大小与构件截面的形状、尺寸、制造方法和加工过程等有关[11]。

本文通过改变模型的局部弹性模量来模拟残余应力对模态的影响。清华大学的杨文，石永久等人通过试验研究得到了焊接工字钢翼缘和腹板的残余应力分布和变形[12]，通过变形和应力的关系可以得出弹性模量因残余应力的存在变为原来的1/4不等，且残余应力主要集中在翼缘及腹板的中心和边缘处，考虑到构件中的残余应力可能过大甚至达到钢材的屈服强度，所以本文在有限元模型中将焊接工字钢梁翼缘与腹板焊接连接处、腹板中心处和翼缘边缘处的弹性模量分别减小为初始模量的1/4，1/10，以便研究在最不利状态下焊接工字钢梁的模态，如图5所示。

图5 工字钢梁考虑残余应力时的前四阶振型

从图5中可以看出，在施加了残余应力后，第二、四阶振型变化较大，发生了明显扭转。第一阶振型，工字钢整体在xz平面内向x轴正方向发生弯曲，上翼缘绕z轴发生轻微逆时针扭转，下翼缘绕z轴发生轻微顺时针扭转。第二阶振型，绕工字梁中心呈中心对称，整体绕z轴发生顺时针扭转。同时，上翼缘在xz平面内向x轴正方向发生弯曲，下翼缘在xz平面内向x轴负方向发生弯曲。第三阶振型，工字钢梁整体在yz平面内朝y轴正方向发生弯曲，没有扭转现象。第四阶振型，相对腹板中心线对称，上下翼缘分别绕其中心线发生中心对称翘曲，腹板发生鼓曲，方向朝x轴负方向，且鼓曲最大位移处在腹板中上部。

完善模型与考虑残余应力影响的焊接工字钢梁频率及其变化率，如表2所示。

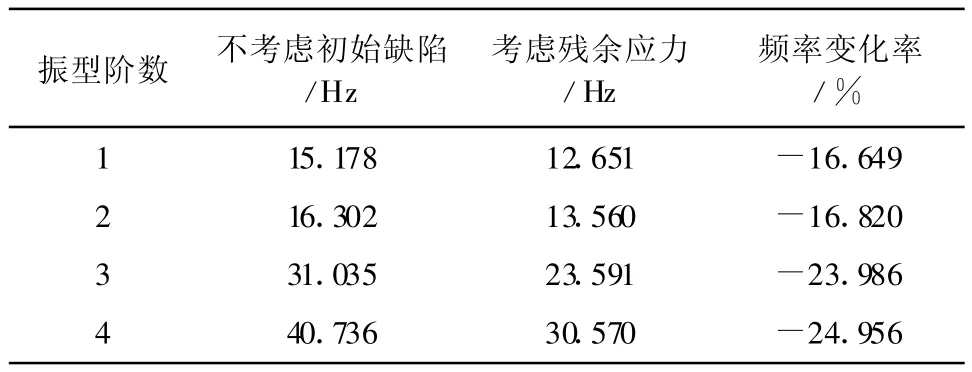
表2 考虑残余应力影响的工字钢梁前四阶频率对比

从表2中可以看出，考虑残余应力时，构件自振频率明显降低，各阶频率变化率随阶数的增加而逐渐增大。可见，残余应力对焊接工字钢梁的模态影响很大，到第四阶振型时频率已达到24.956%的偏差，所以在结构自振分析时不能忽略残余应力的影响。

1.4 同时考虑初弯曲和残余应力对模型模态的影响

考虑残余应力的同时在模型上施加初弯曲的影响，得出的各阶振型与只有残余应力影响的各阶振型类似，在此不予列出。

完善模型与同时考虑残余应力及初弯曲影响的焊接工字钢梁频率及其变化率如表3所示。从表3中可以看出，同时考虑初弯曲及残余应力影响的焊接工字钢梁的频率变化率与只考虑残余应力的模型相差无几，再次论证了初弯曲对焊接工字钢梁模态的影响甚微，而且两种初始缺陷的作用可以简单叠加，没有明显相互影响。

表3 同时考虑残余应力及初弯曲的工字钢梁前四阶频率对比

2 总 结

(1)初弯曲和残余应力对两端固结的焊接工字钢梁的模态有一定的影响。其中残余应力对构件的模态影响尤为明显，各阶振型都发生了变化，而且振动频率变化幅度较大，随阶数的增加而增加，最大的变化幅度可达到24.956%，说明残余应力对焊接工字钢的模态影响不能忽略。

(2)初弯曲对焊接工字钢梁的模态影响不大，各阶振型的变化幅度最多只有0.834%，可以近似忽略。所以工程中可以不考虑初弯曲对焊接工字钢梁模态的影响。

(3)初弯曲和残余应力两种初始缺陷对焊接工字钢梁模态的影响可以相互叠加，没有明显的相互作用。

[1]马 汀，李元齐，罗永峰.建筑钢结构健康检测与鉴定现状[J].建筑结构，2006，36(S1):427-430.

[2]高永毅，苏志霄，焦群英，等.残余应力对构件固有频率影响的讨论[J].机械强度，2002，24(2):289-292，304.

[3]李文威，董学武，王东强，等.铸铁构件固有频率与其残余应力关系的研究[J].中原工学院学报，2007，18(2):7-10.

[4]孙 强，张本福，姚小刚.初弯曲对杆件动力性能的影响[J].工业建筑，1998，28(3):15-17.

[5]陈 骥.钢结构稳定理论与设计(第四版)[M].北京:科学出版社，2001:49-55.

[6]唐宝富.天线结构模态分析[J].电子机械工程，2001，(4):21-24.

[7]张子明，周星德，姜冬菊.结构动力学(第五版)[M].北京:中国电力出版社，2009:61-62.

[8]王新敏.ANSYS工程结构数值分析[M].北京:人民交通出版社，2007:501-502.

[9]中华人民共和国建设部.GB50017-2003.钢结构设计规范[S].北京:中国计划出版社，2003:120-121.

[10]龚治国，高润东，赵 鹏.模态分析在钢梁损伤识别中的应用试验研究[J].住宅科技，2011，(S1):28-30.

[11]曹平周，朱召泉.钢结构(第三版)[M].北京:中国电力出版社，2008:125-126.

[12]杨 文，石永久，王元清，等.结构钢焊接残余应力三维有限元分析[J].吉林大学学报，2007，37(2):347-352.