基于CFD的防淘墙河床冲刷模拟方法
王 帅,张社荣,戚 蓝,王高辉
(天津大学水利工程仿真与安全国家重点实验室,天津300072)
0 引 言
在泄水建筑物及导流洞出口下游设置防淘墙是保护岸坡,防止坡脚发生冲刷的有效措施,但是在水流、波浪等的作用下,防淘墙附近河床仍会发生冲刷,河床下切,使得防淘墙暴露于基岩外部,严重时会导致防淘墙及上部建筑失稳,进而造成岸坡坍塌。因此研究河床的冲刷问题对于防淘墙的设计具有重要意义。
目前河床冲刷主要集中在两个方面:①下游为岩石河床时,其冲刷过程大致为:射流作用于岩石河床上,强烈的脉动水流进入岩石缝隙并沿缝隙传播,产生的脉动压力促使岩石解体与出穴,从而造成河床冲刷,最有代表性的是刘沛清[1-3]等挑射水流对岩石河床的冲刷研究;②下游为深覆盖层河床时,其冲刷相对简单,多采用模型试验[4]或经验公式[5]进行研究。然而,考虑到模型试验费用高、周期长的特点,以及针对防淘墙前河床冲刷经验公式的匮乏,使用CFD技术对河床冲刷进行数值模拟为本研究提供了一条更加可行的途径,如邓军[6]等通过建立冲刷坑底部压力、流速和冲刷深度的平衡关系模拟了射流对二维河床的冲刷,并进行了实验验证;陈小莉[7]等以实际平衡冲坑为边界条件,通过CFD技术模拟了桥台局部冲刷,并研究了坑内的水流运动;凌建明[8]等使用CFD模拟了圆柱形桥墩附近三维流场,针对水流对河床的冲刷,给出了桥墩附近床面的剪切应力分布。以上研究多是集中于桥墩、丁坝等建筑,防淘墙作为一种有效的护岸工程,其冲刷研究相对较少。
本文针对下游河床为深覆盖层的情况,结合实际工程,运用CFD技术,通过建立导流洞下游河床三维模型,对防淘墙附近河床的冲刷进行数值模拟,初步探讨了导流洞按设计洪水导流时冲刷坑的形成,为防淘墙设计提供理论依据。
1 数学模型
1.1 CFD模型
三维水流的控制方程组用不可压缩流体的连续方程和动量方程来表示,在笛卡尔坐标系下其形式如下:
连续性方程:

动量方程:
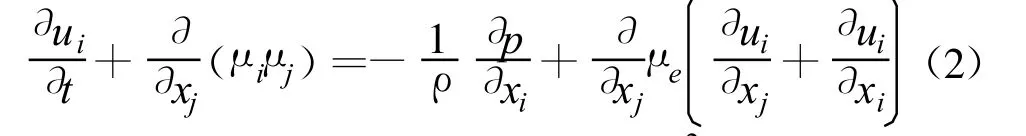
k方程:
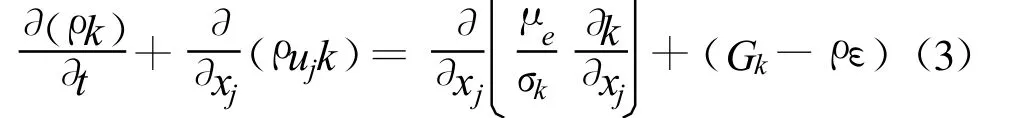
ε方程:
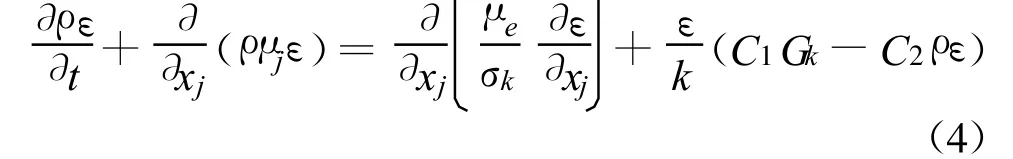
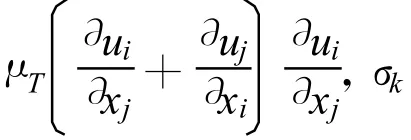
1.2 冲刷坑的形成及控制
在冲刷过程中,冲刷坑底部水流流速会随着冲刷坑深度的增加而逐渐减小,当冲刷坑发展到稳定状态时,意味着冲刷坑底部流速与颗粒临界起动流速之间达到了一种平衡关系。其关系式如下:

式中:u为冲坑底部水流时均流速;uc为床面颗粒临界起动流速。
根据王兴奎[9]等从床面颗粒受力平衡的观点推导出起动流速的一般表达形式为:
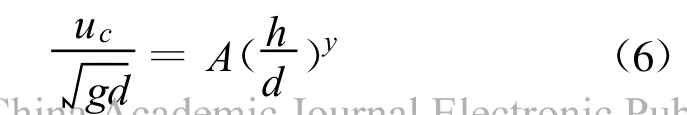
式中:h为水深;d为颗粒粒径;A与y分别为待定常数和指数,由床面颗粒决定,其中颗粒粒径采用d50时 ,A=0.146,y=0.586;颗粒粒径采用d96时,A=1.006,y=0.167。
将式(6)带入式(5)得出冲刷坑底部时均流速与冲刷坑水深之间的平衡关系式:
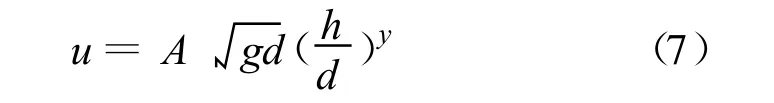
式(7)便可作为对冲刷坑发展过程中控制冲坑底部边界运动的条件。
定义:
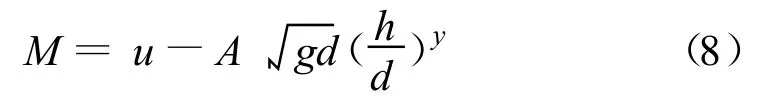
式(8)可用来作为判断河床是否遭受冲刷的控制方程。M >0说明该节点处水流流速大于颗粒起动流速,该处河床发生冲刷,节点下移H;反之(M≤0),该处河床未发生冲刷,节点不动。当所有冲刷坑底部节点都不满足下移条件时,计算终止,此时冲刷坑达到稳定状态。
节点下移距离H通过水下休止角来确定:H≤Rcot φ,式中:H为节点下移距离;R为节点水平间距;φ为床面颗粒水下休止角。
床面颗粒的水下休止角则通过金腊华[10]等提出的散粒体均匀沙的水下休止角公式来计算:
当d≤10 mm时,φ=36.06+4.66lgd;
当d>10 mm时,φ=40.06+0.97lgd;
1.3 边界条件及初始条件
模型的进口边界通过控制上游水位,采用进口流量边界条件来实现。
出口边界采用出流(Outflow)边界条件,其实质是由orlanski提出[11]的sommerfeld辐射边界条件,认为:
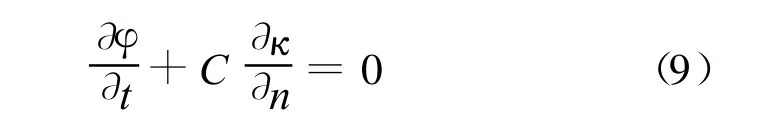
其中:φ为所要辐射的变量,在此为速度U;C为波浪传播速度;n为辐射边界的法向向量。
自由表面:水面与空气接触表面即为自由表面,采用VOF法[12]来处理。该方法涉及多相流理论,在每一个网格用一个变量F来标志它的状态。当F=1时表明网格内充满液体,F=0时表明网格内无液体存在,当0<F<1时表明网格包含自由表面。F函数可通过下述方程得到:

固体边壁采用壁函数处理:
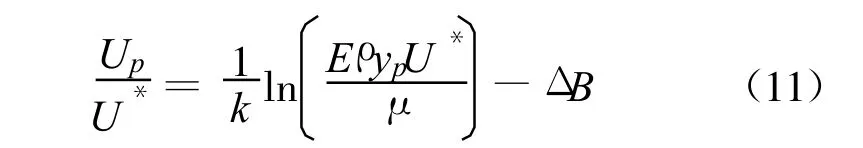
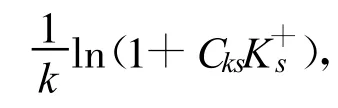
计算区域水流初始流速为断面平均流速。
1.4 基于CFD的防淘墙河床冲刷分析
FLOW 3D采用有限差分法对控制方程进行离散,压力速度求解采用GMRES[13]法,时间差分采用全隐格式。求解过程为:河床未冲刷时,水流达到稳定状态,获得计算区域各节点流场参数,以式(8)判定其是否发生冲刷,若M>0,则该节点下移 H;反之,节点不动。调整计算模型,返回第一步重新计算流场参数,循环计算直到所有节点满足河床不冲刷条件,如图1所示。
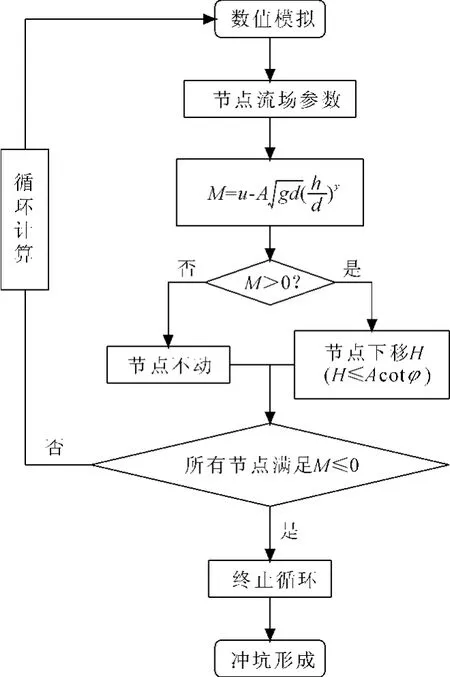
图1 基于CFD的河床冲刷分析流程
2 基于CFD技术的河床冲刷模拟
2.1 基于CFD技术的冲刷模拟验证
采用丁坝局部冲刷实验结果[14]验证采用CFD模拟冲刷坑的可行性。实验所用水槽长10 m,宽0.4 m,模型沙粒径d50=0.94 mm,全水槽铺设6 cm厚,模型丁坝长7.5 cm,宽 1.8 cm,高 3.0 cm,间距15 cm布设于水槽右侧边墙,如图2所示,水槽流量5.83 L/s,平均水深5.0 cm。
为使冲刷坑达到稳定状态,实验要有足够长的水流冲刷时间。通过对水槽中部丁坝周边河床进行测量,图3给出了河床冲刷坑顺水流向A-A(丁坝横向)剖面、垂直河流向B-B(丁坝轴向)剖面形状与数值模拟计算剖面形状对比图。
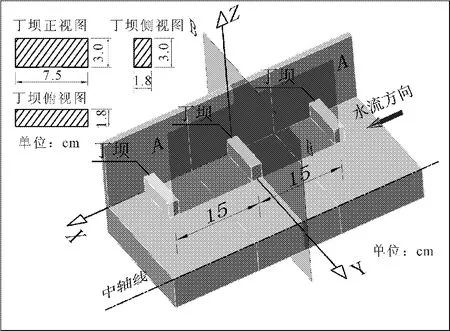
图2 丁坝局部冲刷三维示意图
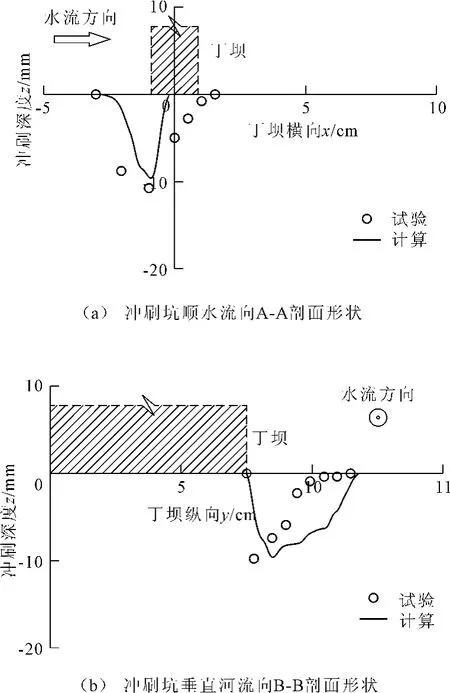
图3 冲刷坑剖面形状对比图
从图3中可以看出,实验与数值模拟得出的河床冲刷坑均位于丁坝端偏向上游。计算所得冲深最大值与实验值相比略小,计算值为9.54 mm,实验值为11.0 mm,相对误差为13.3%。冲刷坑位置与实验结果相同,最大冲深计算值与实验值相近,冲刷坑性态相似但存在一定差异,一方面是由于床面颗粒起动具有一定的随机性;另一方面,在相同流速情况下,颗粒顺坡起动要较水平床面起动容易,逆坡起动则相对较难些;同时数值模拟是建立在颗粒粒径相对均匀的基础之上的,与模型试验采用的非均匀沙有一定出入。但就冲坑位置、冲刷深度以及冲坑形成规律而言,采用CFD技术模拟深覆盖层河床冲刷具有一定的可行性。
2.2 基于CFD技术的防淘墙河床冲刷模拟
将该法应用于某电站导流洞下游防淘墙附近河床的冲刷中。基本资料如下:导流洞出口下游左岸布置一道混凝土挡墙。在挡墙基础中设一道混凝土防淘墙(见图4),长140 m,深12m,厚3m,防淘墙底高程1 293.0m,顶高程1305.0 m。该段河床平均高程1 305.0 m,下游河道自然顺直,左岸边坡自然坡度40°~50°。河床覆盖层由冲积漂卵石组成,颗粒粒径d96=10 mm,厚度3.0 m~10.0 m,河道中央覆盖层较厚(见图5)。
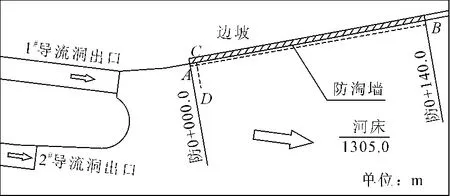
图4 防淘墙平面布置图
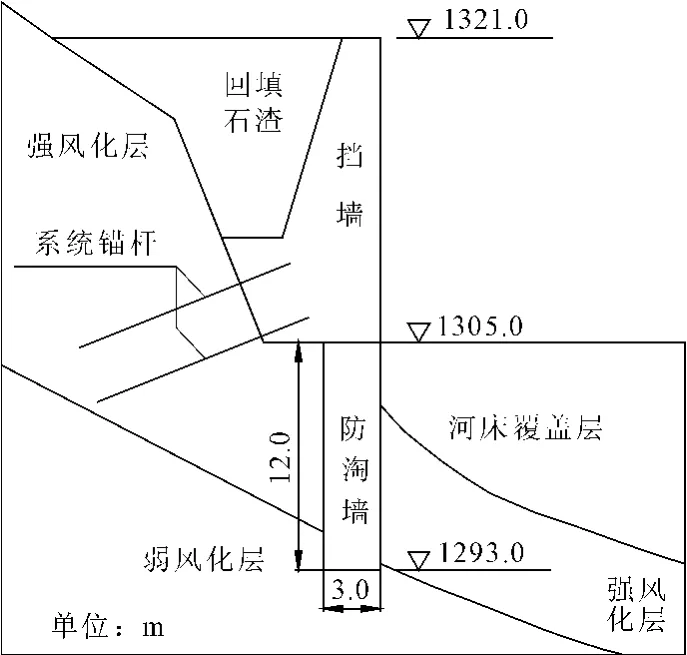
图5 防淘墙横剖面图
建立防淘墙区域河床三维模型,如图6所示,模型选取导流洞出口到防淘墙下游125 m处,模型全长444.5 m,宽472.0 m,高237.5 m,按全年 P=5%的设计洪水标准,相应导流流量7 180 m3/s,下游水位1 317.6 m,平均水深12.6 m。
计算网格为470×410×250,如图7所示,X方向上网格长度为0.4 m~3 m,Y方向上网格长度为0.4 m~3 m,Z方向上网格长度为0.2 m~1 m。采用重点区域局部加密,边缘区域适当放宽的原则。

图6 防淘墙区域三维模型
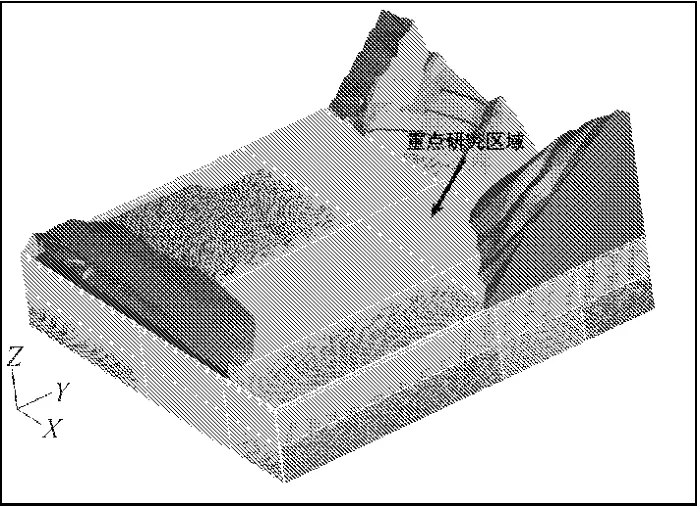
图7 计算网格剖分
追踪床面部分关键点M值随冲坑发展的变化过程,如图8所示。
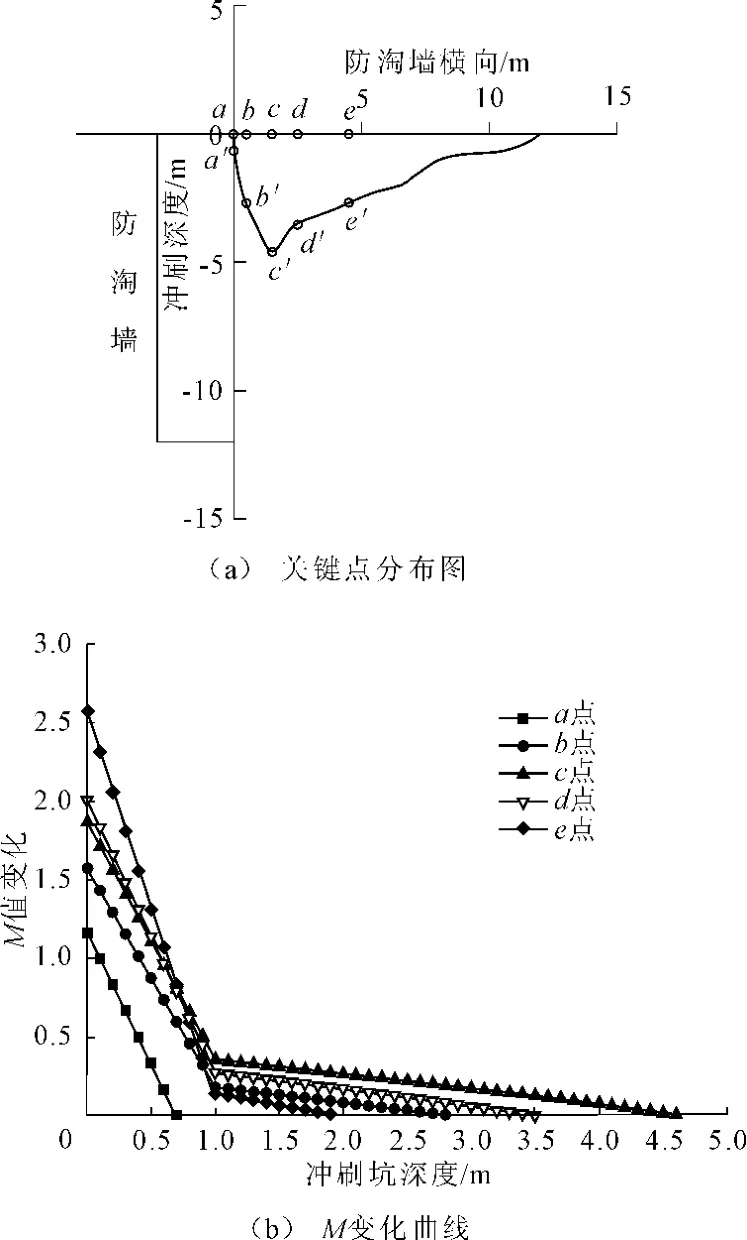
图8 沿C D线剖面关键点的M值随冲坑发展的变化过程
图8(a)给出了沿CD线(见图4)防淘墙横剖面中关键点分布情况,其中c′点为床面c点在冲刷坑底部的投影(a,b,d,e同),图8(b)为 c点向c′点移动过程中M值的变化曲线(a,b,d,e同)。由图可知,河床未冲刷时,各点的M值都较大,当冲深1 m后,M大幅下降,随着冲坑深度的不断加深,M不断减小,并最终等于0,此时冲刷坑达到稳定状态,距离防淘墙1.5 m处的c点冲坑最深。
图9给出了沿防淘墙纵向AB线(见图4)剖面中 J(h 、i、k 、l)点向 J′(h′,i′,k′,l′)运动过程中 M值的变化曲线。从图中可以看出,各点的M值在河床未冲刷时较大,河床冲深1 m后,M值大幅下降,并随着冲坑深度的不断增加而减小,最终等于0,冲坑达到稳定状态,在防淘墙0+004.0处的j点冲坑最深。
图10给出了防淘墙河床在不同深度下的冲坑形态。可以看出,防淘墙附近河床的冲刷主要集中于防淘墙的上游河床,在导流洞出口、防淘墙起始部位的河床冲刷较为严重,形成一个形似椎体的冲刷坑,而下游河床基本未受到冲刷。
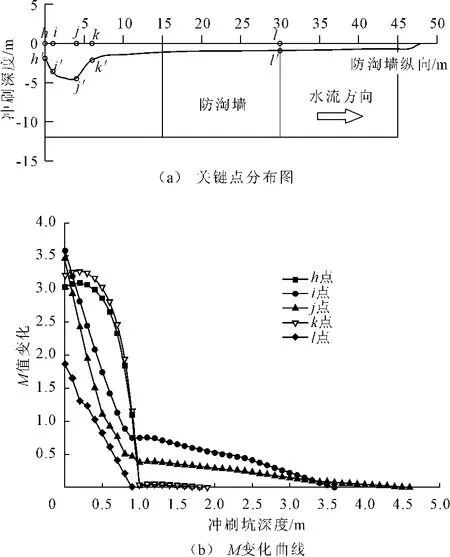
图9 沿AB线剖面关键点的M值随冲坑发展的变化过程
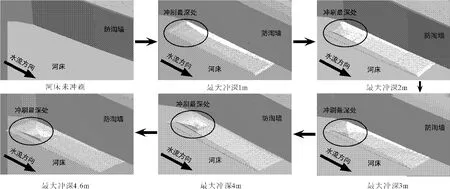
图10 冲刷坑发展过程
图11给出了沿 AB线(见图4)、CD线(见图4)冲刷坑剖面的最终形态。在图11(a)中,沿 AB线剖面距防淘墙1.5 m,原点处即为防淘墙起始端,水流对防淘墙上游部位河床产生冲刷,冲刷部位主要集中于防0+000.0~防0+050.0段,其中防0+000.0~防0+005.0段冲刷较为严重,冲深最大值为4.6 m,位于防0+004.0处。图11(b)中,沿 CD 剖面位于桩号防0+0.004.0处,可以看出,距离防淘墙12 m范围内的河床发生冲刷,冲刷最深处距防淘墙1.5 m。防淘墙附近的河床冲刷仅限于覆盖层,并未对河床基岩造成冲刷。
3 结 论
本文依托工程实例,基于CFD技术,从流速角度对深覆盖层河床冲刷进行了研究,为河床冲刷的数值模拟提供了一种新的思路。研究结果表明:
(1)以冲坑底部流速与临界起动流速之间的平衡关系作为判断河床发生冲刷的控制条件,基于CFD技术,对深覆盖层河床进行了数值模拟。与文献[14]中丁坝局部冲刷实验结果进行对比,采用CFD技术模拟深覆盖层河床冲刷具有一定的可行性。
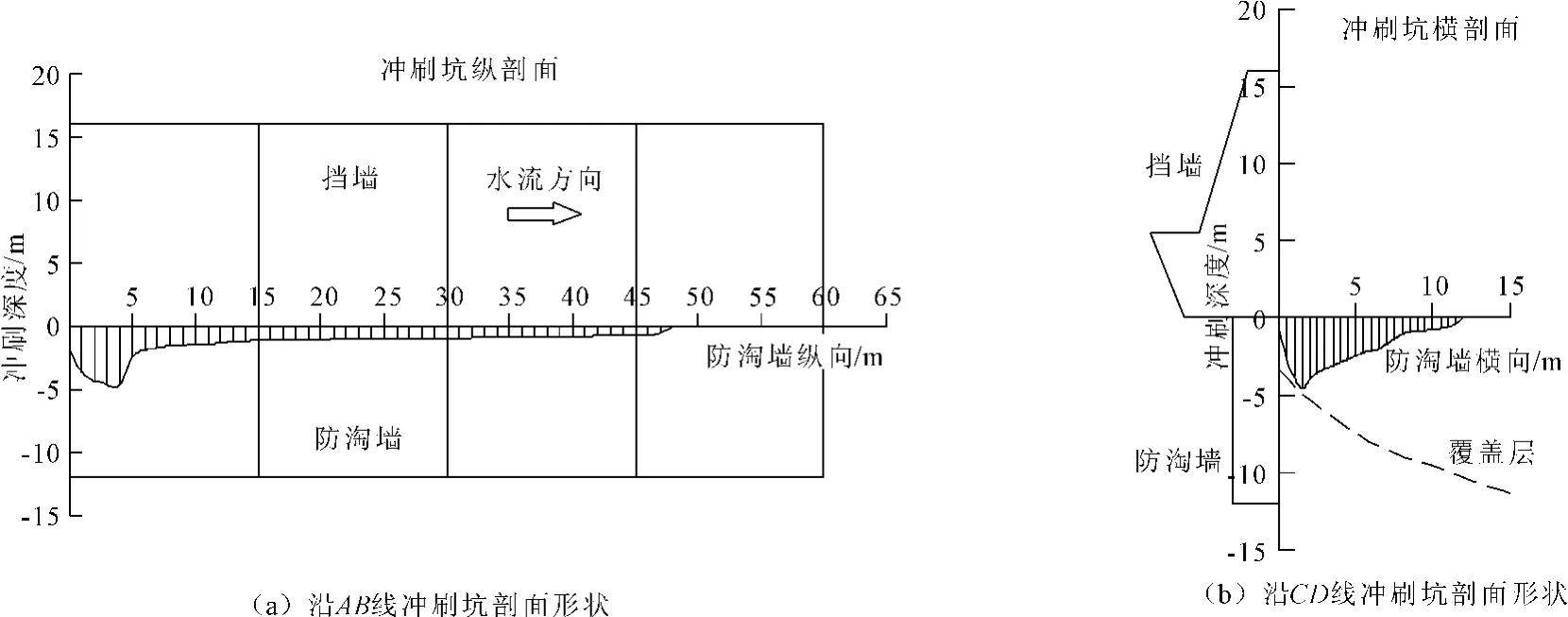
图11 冲刷坑剖面
(2)对某电站导流洞下游防淘墙河床冲刷进行了数值模拟,导流洞按全年P=5%的设计洪水导流时,防淘墙桩号防0+000.0~防0+050.0段河床发生明显冲刷,其中在防0+000.0~防0+005.0段河床冲刷尤为严重,在防0+004.0、距防淘墙1.5 m处河床形成一个形似圆锥体的冲坑,冲坑最深处达4.6 m,该处覆盖层厚4.9m,水流并未冲刷到河床基岩。
(3)通过数值计算结果与模型实验进行对比,可以看出,就目前技术水平而言,数值计算在某些方面可以替代模型试验。首次将数值模拟手段应用于防淘墙设计中,为防淘墙埋深提供设计依据,对降低防淘墙的设计周期与成本具有重要意义。
[1]李爱华,刘沛清.脉动压力在消力池底板缝隙传播的瞬变流模型和渗流模型统一性探讨[J].水利学报,2005,36(10):1236-1240.
[2]李爱华,刘沛清.岩石河床在冲击水流脉动压力作用下的解体破坏机理[J].水利学报,2007,38(11):1324-1328.
[3]李爱华,刘沛清,许唯临.复杂裂隙网络内冲击射流脉动压力传播过程数值研究[J].四川大学学报,2009,41(5):36-41.
[4]沈 波,艾翠玲,田伟平,等.小桥涵自由式出流冲刷试验[J].长安大学学报,2007,27(3):61-66.
[5]詹义正,王 军,谈广鸣,等.桥墩局部冲刷的试验研究[J].武汉大学学报,2006 ,39(5):1-4,9.
[6]邓 军,许唯临,杨忠超,等.基岩冲刷的数值模拟[J].水科学进展 ,2005,16(1):47-51.
[7]陈小莉,马吉明.桥台局部冲刷坑内水流运动的三维数值模拟[J].水动力学研究与进展,2007,22(6):689-695.
[8]凌建明,林小平,赵鸿铎.圆柱形桥墩附近三维流场及河床局部冲刷分析[J].同济大学学报,2007,35(5):582-586.
[9]王兴奎,陈稚聪,张 仁.长江寸滩站卵石推移质的运动规律[J].水利学报,1992,(4):32-38.
[10]金腊华,石秀清.试论模型沙的水下休止角[J].泥沙研究,1990,(3):87-93.
[11]Orlanski I.A simple boundary condition for unbounded hyperbolic flows[J].Journal of Computational Physics,1976,21:251-269.
[12]王永学.VOF方法数模直墙式建筑物前的波浪破碎过程[J].自然科学进展:国家重点实验室通讯,1993,3(6):553-559.
[13]Saad Y,SchultzM H.GMRES:A generalized minimal residual algorithm for solving nonsymmetric linear systerms[J].SIAM Journal on Scientific and Statistical Computing,1986,7:856-869.
[14]彭 静,玉井信行,何原能久.丁坝坝头冲淤的三维数值模拟[J].泥沙研究,2002,(1):25-29.

