温度监测层数对坝体线膨胀系数反演影响

刘 杨 ，李 含 ，孔令娇

(1.河海大学水文水资源与水利工程科学国家重点实验室，江苏南京210098；2.河海大学水利水电学院，江苏南京210098)

0 引 言

由于施工控制、现场具体情况以及坝体自身特点等不同，使得大坝实际的混凝土线膨胀系数与通过试验或经验公式而得到的参数往往存在差异。因此，在大坝安全监控中，对大坝的混凝土线膨胀系数的反演就尤为重要。其反演方法主要有常规反演法和确定性模型反演法[1]。而在确定性模型反演法中，坝体混凝土线膨胀系数的反演与坝体混凝土线膨胀系数的调整参数紧密相关，因此，温度位移分量确定性模型如何建立以及混凝土线膨胀系数调整参数如何求得就凸显重要。

在研究与实践中发现，当坝体内布设温度监控仪器的层数不同时，所建立的相应的温度分量确定性模型的调整参数会有一定程度的改变，从而根据确定性模型所反演得出的坝体混凝土线膨胀系数亦会有一定的变化。本文试以函数拟合法[2]建立坝体温度场，以相关数学分析来解释在坝体温度计布设层数不同的情况下所建立的相应温度位移分量确定性模型的调整参数不尽相同的现象，为坝体混凝土线膨胀系数在同一坝体的不同的确定性模型反演分析中的变化提供合理的理论解释。

1 基本原理以及问题的提出

在无约束条件的情况下，由于变温T而弹性体内各点将发生正应变α T，其中α为弹性体的线膨胀系数。在各向同性体中，系数 α不随方向而变化，这样弹性体中各点的应变分量即为

用有限元计算坝体温度位移时，可将坝体看成弹性体，当坝体网格剖分足够细化时，整个结构的平衡方程组[3]为:

δT为温度位移列阵，而变温结点等效荷载列阵 RT为:

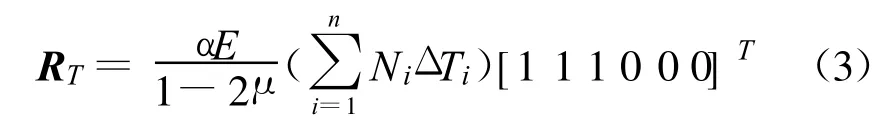
由上式可以看出:由于劲度矩阵K取决于尺寸和弹性常数，因此，在变温T作用下，坝体内任一点位移δT与各点的变温值呈线性关系[4]。

在温度位移分量的确定性模型[5]中，为避免因个别温度计失效而造成误差影响精度以及减少监测数据处理工作量，会用等效温度的方式代替各温度计变温值，进而得到温度位移分量。采用等效温度来计算温度分量时，表达式如下:

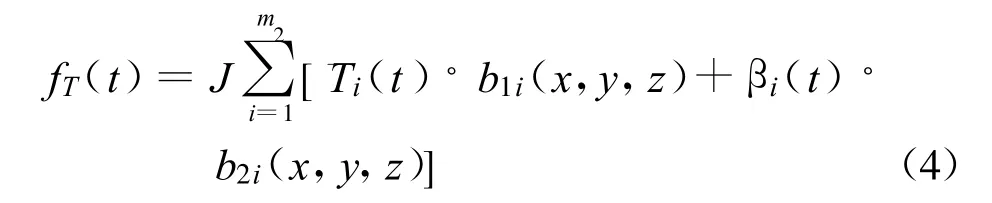
其中，温度载常数b1i，b2i是假设的坝体混凝土材料热力学参数即其线膨胀系数αc0并利用有限元计算得出，是利用有限元计算的单个温度计的单位变温或者单层温度计的单位等效温度在变形测点的位移；而混凝土线膨胀系数调整系数J是来调整计算出的δT与其真实值的差别。本文即用等效温度来计算温度分量。

在确定性模型反演法中，混凝土线膨胀系数 αc即根据公式(5)推求得出。

由式(2)、式(3)、式(4)知，对于坝顶测点位移来讲，其为各变温作用下并根据叠加原理而得到的温度位移分量。分析表明，除了热力学参数会直接影响到温度位移分量的计算外，温度观测层数m2的数量以及在其影响下对大坝温度场整体的插值逼近也是很重要的影响因素。从而解释当温度计布设层数不同时，所建立的温度位移分量确定性模型中的调整参数会有所不同，即反演得出的线膨胀系数会有不同。

2 建立温度场

2.1 温度场函数拟合法

在大坝运行稳定期时，混凝土坝体内的温度场是按照一定的规律呈周期性简谐变化，即可分为稳定温度场和准稳定温度场[6]。因此坝体温度场可以用周期函数(三角函数)与多项式所(三次)组成的函数 fT(x，y，z，t)来表示，即用函数拟合的方式来得出坝体温度场。

本文以中高纬度地区某混凝土重力坝为研究对象，该坝高96 m，坝前水深常年保持在80 m左右。为突出重点、简化计算，选择该坝体某一垂直于坝轴线的横断面作为温度观测断面来研究。该断面即为二维平面模型，则该观测断面不计沿坝轴线方向坐标(Z)。本文以等效温度(平均温度与温度梯度)来拟合该断面坝体温度场，则该断面沿上下游方向的测点温度皆以等效温度的形式表达，所以该坝体断面的温度场函数即为关于坝体高程y与时间t的函数。为方便研究，故将温度场函数表达形式分解为关于平均温度的坝体平均温度拟合函数与关于温度梯度的坝体温度梯度拟合函数，则坝体温度场拟合函数如下所示:

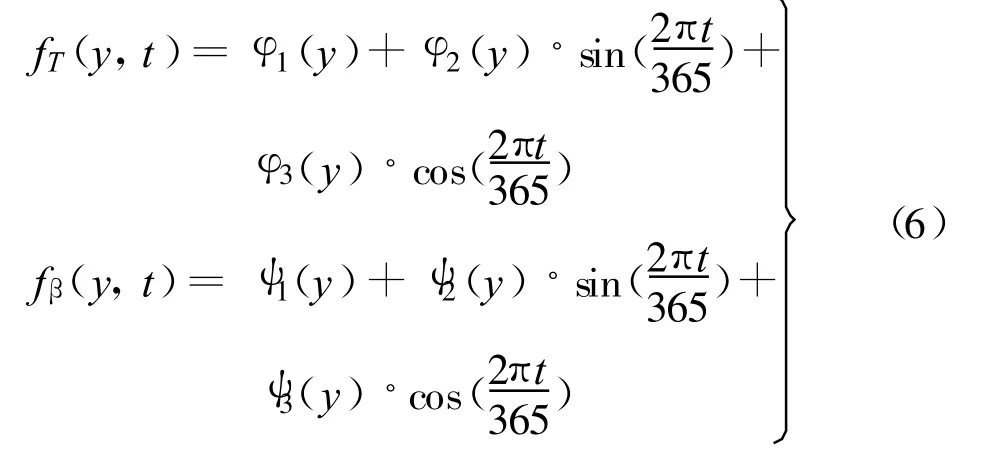
其中，f¯T(y ，t)为坝体平均温度拟 合函数，fβ(y ，t)为坝体温度梯度拟合函数。式中:φi(y)=a0i+a1i◦ y+a2i◦ y2+a3i◦y3，i=1 ，2 ，3 ；ψi(y)=b0i+b1i◦y+b2i◦y2+b3i◦y3，i=1，2，3；y 为坝体断面高程坐标；t为与监测初始日之间的天数。

2.2 拟合温度场

为了函数拟合温度场取得更多样本值，故对该大坝此观测断面应用HYPERMESH工程软件建立二维数学模型。并应用FORTRAN语言将气温、水温、坝前水位(常年固定水位)等50年的大坝边界条件编写子程序SUBROUTINE带入ABAQUS工程软件[7]中，根据热传导原理(其中，坝体混凝土与空气接触表面放热系数 β为60 kJ/(m2◦h◦℃)，与水接触表面放热系数 β为1 400 kJ/(m2◦h◦℃))及相应的边界条件并利用有限元法，从而计算出该大坝坝体50年(1950-01-01至1999-12-31)的温度场(每10 d计算一次)，图1所示为1975-01-20坝体温度场云图，图2所示为1975-07-19坝体温度场云图。

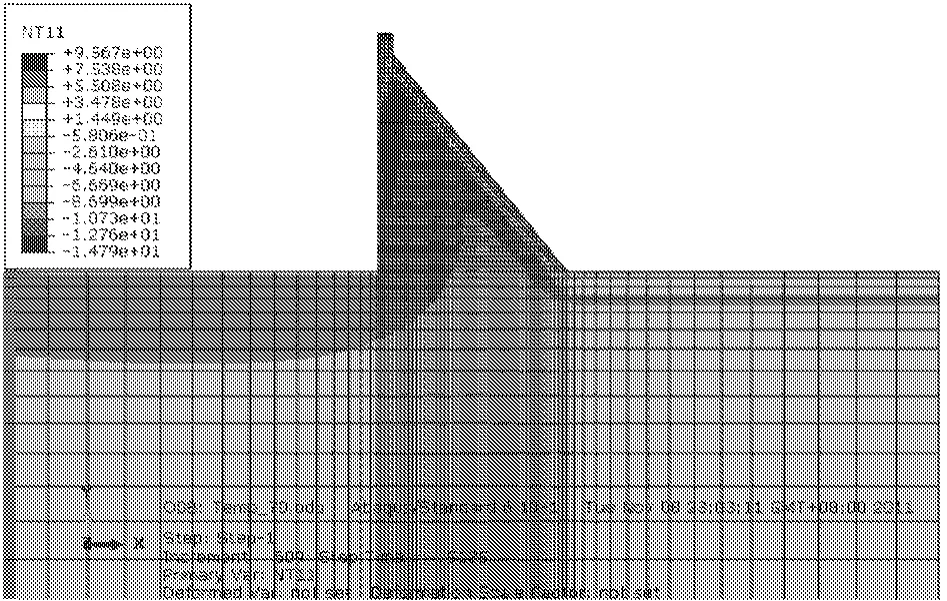
图1 1975-01-20坝体温度场云图

在该坝体温度场中，取出大坝处于运行稳定期的包括坝顶临界层在内的14层坝体结点历时35年(1965年1月1日至1999年12月31日)的温度值样本，由此计算出每层历时35年的随时间变化的平均温度和温度梯度，并以此为函数拟合坝体温度场的样本，应用逐步回归分析法编写程序，利用MATLAB计算软件求出公式(6)中各系数的最佳估计值，从而以函数拟合法求出坝体温度场，如表1所示。

图2 1975-07-19坝体温度场云图

表1 温度场函数拟合结果

本例中坝体温度场拟合函数中的坝体平均温度拟合函数 f¯T(y，t)和坝体温度梯度拟合函数 fβ(y，t)的拟合复相关系数分别达到了0.9919和0.9398，均已是很高的拟合精度并满足置信水平要求，故认为坝体温度场拟合函数对该坝体观测断面温度场的回归拟合是有效的。图3，图4即为1975年1月20日和1975年7月19日经回归拟合的坝体平均温度拟合曲线图和坝体温度梯度拟合曲线图。

3 数学处理及分析对比

以坝顶位移来讲，其为在各层变温作用下根据叠加原理而得到的温度位移分量，而由式(2)(3)(4)可以看出，在某种程度上坝顶测点位移可以进一步的看作坝体各层变温叠加后产生的效应量。为了分析在温度计布设层数不同的情况下，所建立的温度分量确定型模型中各层等效温度对原温度场的逼近程度的差异，笔者做了以下计算:

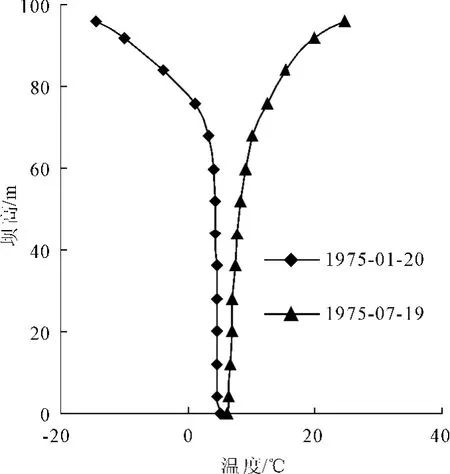
图3 坝体平均温度拟合曲线

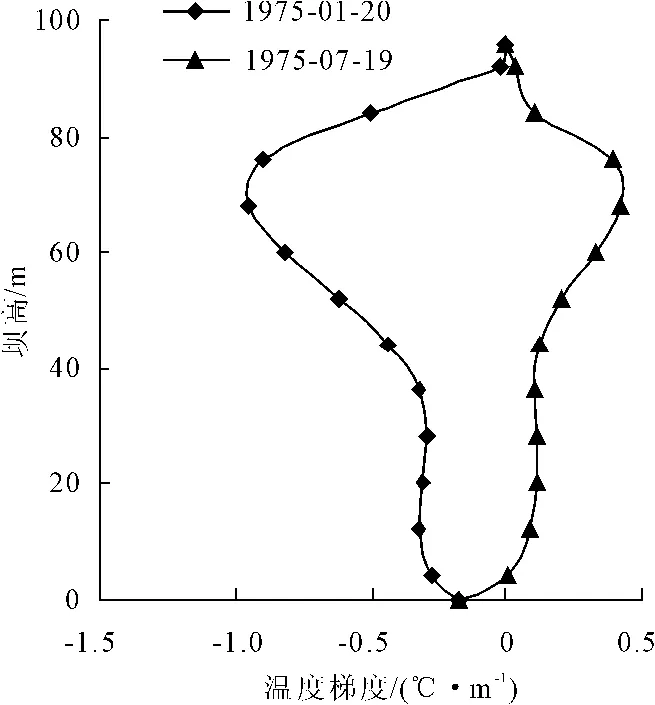
图4 坝体温度梯度拟合曲线

(1)将某个时刻经函数回归拟合得出的温度场中各层变温在坝高方向(y轴方向)积分，即坝体内的温度分布面积，公式为

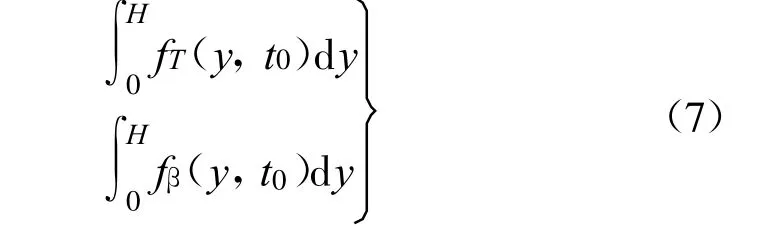
式中:H为坝高；t0为某已知时刻。计算出自1965年1月至1日至1999年12月31日之间的坝体温度分布面积。

(2)当温度计布设层数为 m2=3，4，6，12时，在这四种情况下分别建立确定性模型。根据各层温度观测值计算该层的平均温度和温度梯度，并根据布设有温度计的每两层温度观测值插值出该两层之间的结点温度，且计算出这些中间层的平均温度和温度梯度。进而计算出在温度计布设层数m2分别为3，4，6，12四种情况下，每个观测时刻坝体温度场的等效温度在坝高方向(y轴方向)的累加，即坝体内的温度分布面积，公式为

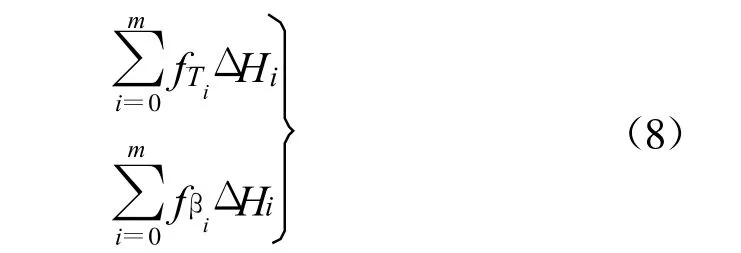
利用该公式计算出当 m2=3，4，6，12时，确定性模型中自1965年1月至1日至1999年12月31日之间四种情况下的以等效温度形式计算的坝体温度分布面积。

并绘制在以上各种情况下的分别关于等效温度(平均温度和温度梯度)的坝体温度分布面积过程线图，本文摘出1980年1月1日至1982年12月31日三年的情况予以分析，如图5、图6。

图5 坝体温度分布面积过程线(平均温度)

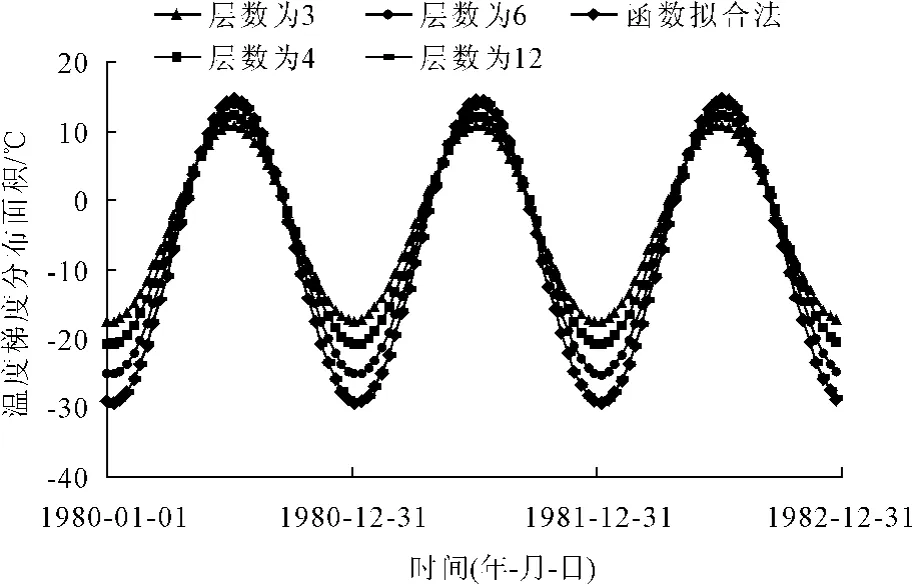
图6 坝体温度分布面积过程线(温度梯度)

经分析可知:

(1)如图5所示，温度计布设层数m2分别为3，4，6，12时，对应情况下确定性模型中的坝体平均温度分布面积值均小于坝体平均温度拟合函数的平均温度分布面积值，并且，当温度计布设层数m2越多时，该情况下的坝体平均温度分布面积值对坝体平均温度拟合函数求出的平均温度分布面积值的逼近程度越高。

(2)如图6所示，温度计布设层数m2分别为3，4，6，12时，对应情况下确定性模型中的坝体温度梯度分布面积过程线的波动幅度皆小于坝体温度梯度拟合函数的温度梯度分布面积过程线的波动幅度，并且，亦是当温度计布设层数m2越多时，该情况下的坝体温度梯度分布面积过程线对坝体温度梯度拟合函数的温度梯度分布面积过程线的逼近程度越高。

由以上两者可得出，在温度分量确定性模型中，所假设线膨胀系数 αc0不变的前提下，当温度计布设层数m2越多，此时建立的确定性模型的坝体等效温度对坝体原温度场的拟合逼近程度越高，而由之前分析可知，随着温度计布设层数m2的增加，温度位移分量的计算值δ′T会逐渐增大并接近真实值δT。并根据温度分量确定性模型中的反演公式(5)及公式(9):

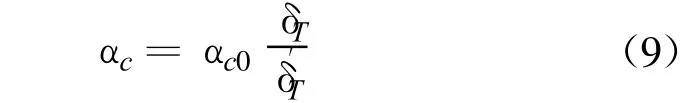
可推出:

则在所假设线膨胀系数αc0不变的前提下，随着温度计布设层数m2的增加，那么调整系数J也会随之逐渐减小且趋近于1。这也就解释了在大坝温度分量确定性模型的建立过程中，当温度计布设层数m2不同时，所得出的调整系数J会有不同的原因。而由式(9)、式(10)可知，反演得出的混凝土线膨胀系数趋于真值。

4 实例验证

为了印证本文论点，作者将该大坝建立数学模型，根据温度边界条件，设坝体混凝土线膨胀系数以有限元法计算坝体温度场和应力场并得出1965年1月1日至1999年12月31日间坝体温度场资料和坝顶温度位移分量资料，并将该所得结果作为真值，则所设坝体混凝土线膨胀系数即定为真值。

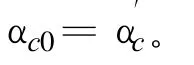
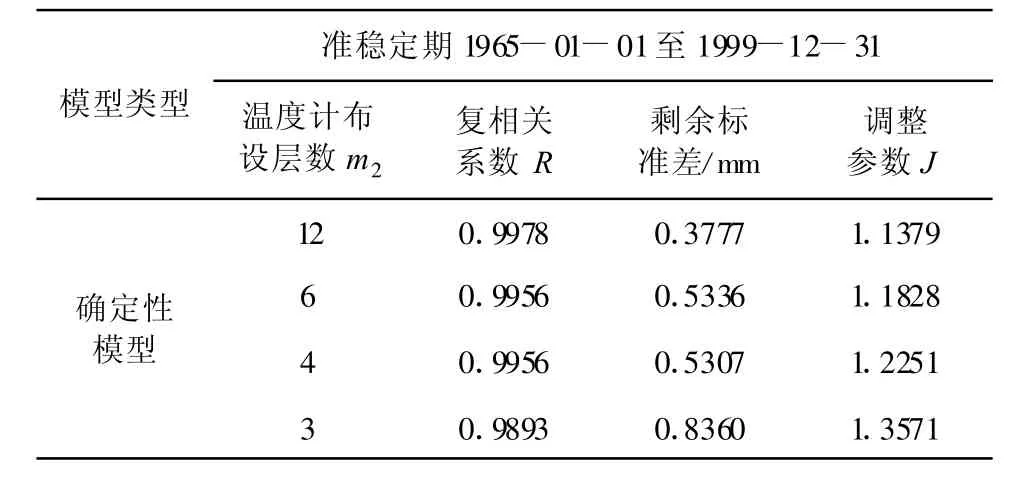
表2 确定性模型计算结果

如表2所示，在4种情况下，温度分量的确定性模型的调整参数J是随着温度计布设层数m2的增大而减小的，并逐渐趋近于1。由公式(5)可知确定性模型反演得出的混凝土线膨胀系数 αc=αco◦J，并且随着调整参数J逐渐趋近于1时，则反演得出的混凝土线膨胀系数 αc逐渐趋于α′c，即趋近于真值。故温度计布设层数的不同也会影响到确定性模型反演法中线膨胀系数 αc的反演。此拟合计算结果与之前理论分析相一致，从而佐证本文结论。

5 结 论

本文以函数拟合法并按照等效温度的形式拟合出坝体温度场曲线，又以确定性模型的建立思路，在坝体温度计布设层数不同的情况下分别根据观测层温度资料内插出坝体温度场，再将两者按照温度分布面积的计算方式进行比较研究，并以实例的温度分量的确定性模型进行参照分析，所得结论如下:

(1)大坝温度位移分量确定性模型的坝体混凝土线膨胀系数调整参数随着坝体温度计布设层数的增大而减小，并逐渐稳定且趋近于1，即温度位移分量逐渐逼近其实际观测值。

(2)对同一大坝在所选温度监测层数不同的情况下，利用确定性模型反演分析得到坝体混凝土线膨胀系数存在一定差异，且随着温度监测层数的增多，所反演出的结果相应趋近真值。

(3)本文所得出坝体混凝土线膨胀系数在具体反演中存在差异性的结论，对坝体材料性态参数的综合分析以及大坝相关方面安全评价具有参考价值。

[1]吴中如.水工建筑物安全监控理论及其应用[M].北京:高等教育出版社，2003:282-287.

[2]郑福寿，沈长松，林益才.求解应力确定性模型中温度分量的函数拟合法[J].河海大学学报(自然科学版)，2000，(5):54-58.

[3]徐芝纶.弹性力学[M].北京:高等教育出版社，2009:120-129.

[4]顾冲时，吴中如.大坝与坝基安全监控理论和方法及其应用[M].南京:河海大学出版社，2006:12-21.

[5]吴中如，刘观标.混凝土坝的位移确定性模型研究[J].大坝观测与土工测试，1987，(1):16-25.

[6]朱伯芳.大体积混凝土温度应力与温度控制[M].北京:中国电力出版社，2003:67-74.

[7]王 建，刘爱龙.ABAQUS在大体积混凝土徐变温度应力计算中的应用[J].河海大学学报(自然科学版)，2008，36(4):532-537.