基于小波分解的OFDM与单载波信号识别

王兰勋，闫姗姗

(河北大学电子信息工程学院，河北 保定 071002)

在通信环境中，调制方式日趋复杂多样，按子载波数的多少可分为单载波调制和多载波调制。在多载波调制技术中，正交频分复用(Orthogonal Frequency Division Multiplexing，OFDM)技术凭借其较高的频谱利用率及较强的抗码间干扰能力而备受人们关注［1］。从目前文献来看，国内外研究学者对单载波信号的调制方式识别研究居多，但是对多载波信号的识别研究相对较少，因此对OFDM信号的识别研究显得尤其重要。文献［1］根据OFDM信号和单载波信号的归一化四阶累积量C42作为特征值进行信号的调制方式识别，在低信噪比的多径信道下实现了较好的识别效果，但是需要在每个信噪比点下设置门限值，增加了算法的复杂度。文献［2］根据单载波信号和OFDM信号所对应的小波脊线具有不同的特征，经过预处理，利用其熵值作为特征值进行信号间的调制方式识别，在低信噪比的短波中等信道下同样达到了较高的识别率，但是基于幅值最大法提取小波脊线运算量较大［2］，无疑造成该识别算法运算速度慢。文献［3］提出对单载波和OFDM信号进行小波变换寻找奇变点，利用OFDM信号的奇异性来达到识别OFDM信号，但是该识别方法是在理想情况下进行的，对噪声的影响也比较敏感。

小波分解是一种多层次的信号分析方法，具有多分辨分析的特点，它既可以分析信号的概貌轮廓特征，又可分析信号的细节特征变化，提供信号局部化的时频域信息，其作为一种特征提取的工具已经得到较为广泛的应用［3］。针对单载波与多载波信号间的识别问题，本文基于小波分解的多分辨率特性，针对OFDM和单载波信号的细节信息在同一分解水平下存在差异这一特点，通过对信号的细节分量具有不同的幅度变化进行仿真分析，并利用其幅度差作为特征参数，并基于最近邻法判决规则实现了单载波和OFDM信号的识别。

1 信号及多径信道模型

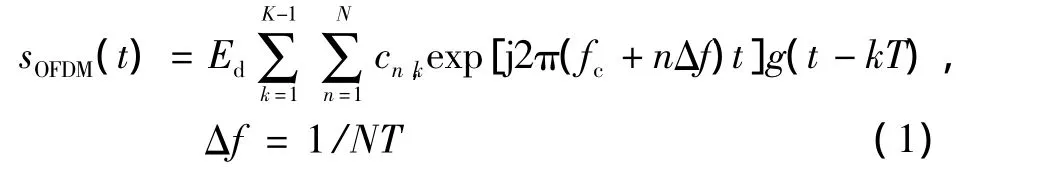
式中:Ed为接收信号的平均功率;g(t)为成型脉冲函数;N是OFDM信号的子载波数目;Δf是相邻子载波间的频率间隔;T为符号周期;cn，k表示OFDM信号第n个符号周期内第k个子载波的符号序列。

针对信号在多径信道下传输，由于多径信道有两个特点:一是给在该信道上传输的信号引入了时延扩展;另一个是它具有时变性。由于存在时延不同的传输路径，使得信号在通过多径信道后在接收端产生衰落。信号经过多径信道的离散等效模型可表示为［4］

式中:h0，θ0分别表示主径的幅度增益和相移因子;hl，θl分别表示第l条路径的幅度增益和相移因子;L表示多径信道的路径数目。在接收机已实现精确的自动增益控制和载波相位同步时，通常取h0=1，θ0=0。

在实际的信道模型中，多径幅度以指数率衰减，即hl=αl(α ≤1，l=0，1，…，∞)，α 为多径衰减参数，多径的相移因子θl在［0，2π］之间随机独立选取。

信号经过多径信道后，接收到的信号可表示为

2 小波分解原理及细节特征提取

小波分解主要基于小波变换的多分辨分析特性，对待识别的调制信号进行多层小波分解，提取信号在各个频率段的特征向量［4］。本文采用多分辨分析的Mallat塔式算法，将信号分解成低频A1和高频D1两部分，然而在下一层分解中，对高频部分暂不予以考虑，只对上一层的低频部分A1做进一步分解，分解成低频A2和高频D2两部分，以下再分解依此类推。一个3层小波分解的结构图如图1所示。

图1 3层小波分解的结构图

根据图1，信号s可以表示为

30例症状性颈动脉狭窄患者的手术均成功实施，术后无再狭窄，无并发症发生。术后1个月无一过性脑缺血发作。术后狭窄率与收缩期峰值流速与术前相比，差异具有统计学意义，P<0.05。见表1及图1、2。

根据小波分解的层数不同，可以得到信号在不同频率通道下的逼近信息和细节信息，各层的细节信息和逼近信息是原始时间序列在相邻的不同频率段的成分［4］。由于多层分解只对低频信息作进一步的分解，因此随着小波分解层数的增加，频率的分辨率也变得越来越高，不同调制类型信号的细节特征在同一分解水平下差异也越来越明显，因此当信号具有不同的频率成分时，可以通过多层小波分解提取识别信号的有效分类特征。而且随着分解层次的增加，在每次分解时信号的长度也随之减半，大大减少了在实际应用中小波变换的复杂度。

根据多分辨分析理论，对调制信号进行小波分解可以得到信号在不同水平下的细节信息。然而，对于长度L的接收信号序列s={sn|n=0，1，…，L-1}，其小波分解为

本文选择Daubechies3小波对待识别信号进行小波分解，Daubechies小波是一种紧支集小波，其局部特性较好。其中{h0，h1，…，hN}，N=5 为 Daubechies3 小波的低通滤波器系数;sm，dm分别为在分解水平m层下的逼近信息和细节信息。D1表示最高频率区域的细节信息，D2次之。随着小波分解水平m层的不断增加，频率分辨率划分的越来越高［5］。本文根据多分辨率分析理论，应用小波技术分解信号，以获得单载波信号和OFDM信号的各层细节信息，如图2所示。

图2a～2d中最上面一层是不同调制方式的信号经小波3层分解后得到的逼近信息系数，即对信号概貌轮廓的描述，第2层至第4层分别表示各个信号经过小波分解后得到的细节分量D1，D2，D3，即信号的细节，是对信号变化的描述，D值大，说明信号变化大，D值小，则说明信号变化小。从图2a～2d中可以看出，单载波信号随着分解层数的增多，细节分量Dm的幅度值呈逐渐减小的趋势，曲线趋于平滑，说明单载波信号变化小;而OFDM信号却不同，从图2e，2f中可以看出，随着分解层数的增加，细节分量Dm的幅度值呈现逐渐上升的趋势，并且随着子载波个数的增多，D值的变化范围也变大。这是由于OFDM信号有若干个子载波叠加而成，并且各个子载波上码元信息互不相关，由中心极限定理可知，随着子载波个数的增加，OFDM信号包络在时域趋近于高斯分布的性质越强，且子载波个数越多，高斯性越强，并与各个子载波调制方式无关［6］，而单载波信号不具有这种性质。利用不同调制方式信号的细节分量Dm在同一分解水平下存在差异这一特点，可以构造特征参数作为识别单载波信号和OFDM信号的分类特征。

图2 OFDM和单载波信号的小波分解

本文利用Daubechies3小波对信号进行小波分解及细节特征提取，Dm(m=1，2，…，M)为第m层的细节分量，本文构造的特征参数为

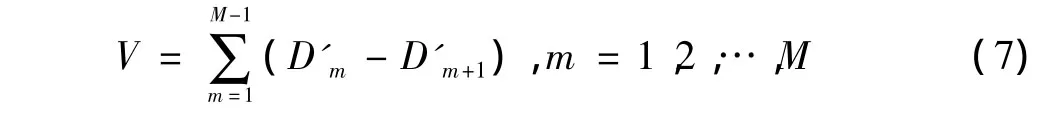
3 仿真分析

本文采用单载波信号包含{MASK，MPSK，MFSK，MQAM(M=2，4)}和 OFDM 信号(子载波数为32，64，128，256)，对特征参数V在理想高斯信道、多径信道下分别进行了MATLAB仿真，并在每个信噪比点做100次蒙特卡洛实验，每组实验数据2048点，然后求取均值，得到在理想高斯信道、多径信道下各信号特征参数V的曲线变化如图3、图4所示。

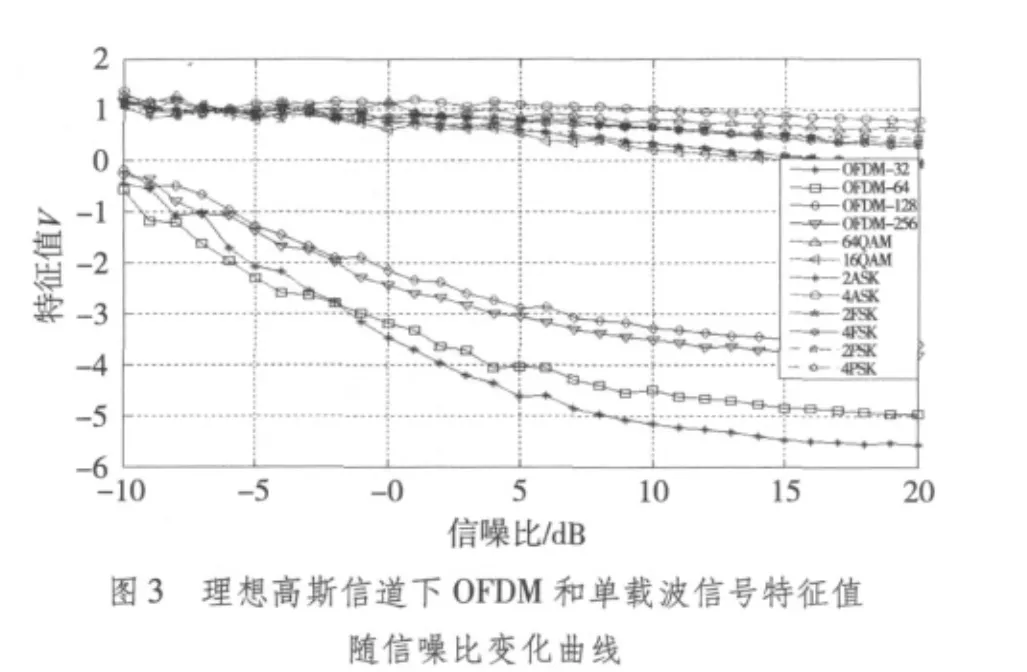
通过比较图3、图4可以看出，在多径信道下，由于受到多径时延、衰减因子、多普勒频移等因素的影响，信号的特征参数V与在理想高斯信道下稍有偏差，但并不影响对OFDM信号的识别，证明该特征参数V在多径信道中具有较好的抗多径衰落能力。

针对特征参数V对OFDM信号与单载波信号的识别效果，采用最近邻法进行分类，最近邻法在原理上属于模板匹配，是用距离远近表示相似程度。它将训练集合中的每个样本作为模板，用待识别样本与每个模板作比较，看与哪个模板最相似(即为近邻)，就按最近似的模板的类别作为待识别样本的类别［7］。虽然它是次优的，但其直观解释相当简单，是实践中广泛使用的一种分类方法。

设置类别数c=2，即ω1，ω2;假定ω1为OFDM信号，该类别包含样本(VOFDM-32，VOFDM-64，VOFDM-128，VOFDM-256);ω2为单载波信号，该类别包含样本(VMASK，VMFSK，VMPSK，VMQAM)。其 中，VOFDM-32，VOFDM-64，VOFDM-128，VOFDM-256，VMASK，VMFSK，VMPSK，VMQAM为不同调制类型信号的理论值。从图4可以看出，单载波信号和含有不同子载波数的OFDM信号的特征值V都集中在两个不同的区域，因此为了减少复杂度，选择单载波信号中V值的最小值、OFDM信号中V值的最大值，即

首先计算待识别信号的V值，比较未知类别样本与所有已知类别样本VSC，VOFDM间的欧氏距离，并判决待识别信号与哪点距离最近就属于哪类。

为了测试所提出的特征参数V对OFDM信号的识别效果，仿真信道采用前面所描述的多径信道模型，6条多径信道幅度参数为 h=［1.000，0.631，0.398，0.251，0.159，0.100］，多径相位因子随机选取，100 Hz多普勒频移，进行MATLAB仿真。信号参数设置:载波频率为3 kHz，符号速率为1000 Baud/s，采样频率为10 kHz，OFDM信号采样32路子载波。信噪比的变化范围为-10～+20 dB，步长为5 dB，进行1000次蒙特卡罗仿真，从而得到在不同信噪比下OFDM信号的正确识别率如表1所示。

表1 不同信噪比下正确识别率 %

从表1可以看出，基于小波分解提取细节特征的方法用于识别单载波和OFDM信号实现了较高的识别率。在-10 dB的情况下均达到90%以上的识别率，仿真中除对含有32路子载波的OFDM信号进行测试，还对含有64路、128路、256路子载波的OFDM信号进行识别率验证，实验结果证明同样具有较高的识别率。

4 结论

本文基于小波分解的多分辨率分析特性，将调制信号进行逐层分解，获取信号的各层细节信息，这些细节信息包含几乎全部的信号变化情况，同时也消除了绝大部分的干扰噪声。另外该参数不受多径时延、衰减因子、多普勒频移等因素的影响。之前的研究都在较高信噪比下进行调制识别，该方法在-10 dB的情况下均能达到90%以上的识别率，证明了该方法在较低信噪比下的可行性。对于不同调制类型的信号具有不同的细节特征以及最近邻法判决规则直观简单，再加上Daubechies3小波良好的正交性，都促使该识别方法在较低的信噪比下同样得到较高的识别效率。

［1］吕挺岑，李兵兵，董刚.一种多径信道下的OFDM信号盲识别算法［J］. 现代电子技术，2007，30(11):13-16.

［2］张传忠，段田东，刘世刚，等.基于小波脊线的OFDM与单载波信号识别［J］. 信号处理，2011，27(7):1100-1105.

［3］刘薇.基于小波的OFDM信号与单载波信号识别技术［D］.哈尔滨:哈尔滨工程大学，2008.

［4］王玉娥，张天骐，白娟，等.基于循环自相关的OFDM调制识别方法［J］. 电视技术，2012，36(5):44-48.

［5］陈健，阔永红，李建东，等.基于小波变换的数字调制信号识别方法的研究［J］. 电子与信息学报，2006，28(11):2026-2029.

［6］张晶晶.基于小波变换的OFDM信号识别技术研究［D］.西安:西安电子科技大学，2009.

［7］赵莹，高隽，汪荣贵，等.一种新的广义最邻近方法研究［J］.电子学报，2004，32(S1):196-198.

［8］LI H，BAR-NESS Y，ABDI A，et al.OFDM modulation classification and parameters extraction［C］//Proc.1st International Conference on Cognitive Radio Oriented Wireless Networks and Communications.Piscataway，USA:IEEE Press，2006:1-6.