基于最大化网络吞吐量的WMN信道分配算法
郑鹏宇,何世彪,戴昊峰,张 晖
(重庆通信学院,重庆 400035)
无线Mesh网络(Wireless Mesh Networks,WMN)是一种新型的Internet无线接入解决方案,被认为是一种很有前途的技术,是一种多跳、具有自组织和自愈特点的宽带无线网络结构,即高容量、高速率的分布式网络[1]。它融合了无线局域网(WLAN)和Ad Hoc网络的优势,支持用户节点和无线接入点(AP)之间的多跳通信,即在WMN中,任何用户节点都可以收发自己的数据分组。WMN作为最后一英里宽带接入的解决方案,有效解决了传统WLAN中存在的可伸缩性差和健壮性差等问题。
而多天线多信道(Multi-Radio Multi-Channel,MRMC)WMN是当前的研究热点,一个多天线多信道WMN[2]是指一个WMN网络中的若干节点配置了多个IEEE802.11标准天线[3-5],因此这些节点可以同时和其邻居节点发送、接收数据。在WMN中,影响网络吞吐量的主要因素是链路间同信道干扰,这种干扰是因为相邻节点在同一时刻使用相同信道而产生的。信道分配的目的就是将可用的正交信道分配给每条链路,以减小链路间的干扰。由此可见信道分配对于提高网络吞吐量起到关键作用。
目前,对于无线Mesh网络的信道分配机制主要分为集中式和分布式分两种,本文主要研究了分布式的信道分配机制。文献[6]采用对每个节点分配同样信道集合的方式来进行信道分配,这种方式虽然易于实现且也能保证网络连通性,但是对于复杂网络的适应性不够;在文献[7]中提出基于负载感知的信道分配策略,但其依附于路由协议联合设计,信道分配前只基于虚链路容量进行评估,考虑相对简单;在文献[8-9]中提出了一种基于CHYA的准静态信道分配方案,但是该方案没有考虑信道干扰,增加了Mesh网络自身的竞争性;文献[10]提出了基于干扰冲突的贪婪信道分配策略,但链路评估时没有考虑网络负载,降低了网络性能。文献[11]提出的SICA分配机制是一种基于干扰感知的分布式分配算法,采用一种在线学习算法,且各节点不需要完备的策略信息。其不足在于算法执行到稳定状态所耗费的时间较长,以及在网络负载较大时需要频繁切换信道来传输数据流的数据包,增加了端到端延时。
针对以上算法中的不足,本文提出了一种基于博弈论的信道分配算法(Game Based Channel Assignment,GBCA),GBCA算法采用联合博弈,能以更快的速度达到收敛状态。通过仿真分析,证明GBCA算法能够很好地避免无线Mesh网络中节点之间和链路之间的干扰,可以较好地改善系统性能(如系统吞吐量、收敛性、丢包率等)。
1 系统模型构建
1.1 网络模型
GBCA算法的目标是最大化网络的吞吐量,系统的吞吐量和系统中的干扰有密切的关系。把WMN模型简化为一个有向图G(V,E),其中V是节点集合,E是网络中的链路集合。节点的通信半径记为rc,侦听半径(干扰半径)记为ri,其中ri=q×rc(q>1)。则当且仅当节点i,j在彼此的通信范围内才存在链路(i,j)。当且仅当两条链路使用同一条信道,且至少有一条链路的一个端点在另一条链路的一个或两个端点的干扰范围内时,两条链路彼此干扰。如图1所示,链路(A,B)使用信道c通信时如果链路(C,D)也同时使用信道c通信,则两条链路彼此之间存在干扰。

图1 WMN网络干扰模型
WMN中的每个节点都有N个无线收发天线,每个天线都可以被调至某个正交信道上用于接收发送数据,可用正交信道数为M。在传输和接收数据时,每个天线都必须分配一个唯一的正交信道,即一个节点的不同天线必须分配不同的信道,所以N<M。
1.2 算法模型
从式(1)所示的香农公式可得,信道容量与带宽和信噪比有关,当带宽一定时,信噪比越大则信道容量越大。所以利用这个特性,可以构建出最大化网络吞吐量的资源分配算法。

对于网络中的一个节点i而言,其传输时是否受到干扰取决于在其传输数据时干扰范围内有无其他节点同时使用相同信道进行数据传输。如果有,节点i的传输就不会成功。假设Ii为节点i干扰范围内的节点集合,=n为集合中结点的个数。令C为可用正交信道的集合,则=M。
通过为每条链路分配合理的流量和信道来最大化网络的吞吐量,也即传输成功的总流量。而成功传输的概率与网络中的干扰有关。对于一条链路(i,j)而言,网络对其造成的干扰主要由接收端j所受到的干扰引起,即Ij中存在与链路(i,j)使用相同信道的节点。如图1所示,对与链路(A,B)使用信道c通信,如果节点A的干扰范围内的节点(节点C,E,F,G,H)有使用信道c通信则会对A造成干扰,同理接收端同样可能收到其干扰范围内节点的干扰。
那么数据成功传输的概率则与信噪比(SNR)有着密切的关系,SNR的表达式为

式中:Gij为链路增益;Δ 为背景噪声[12];f(k,j)是指节点k是否使用和节点j相同的信道,其定义为

对于发送节点i,首先查看其有无到达目的节点的路径,如果有则通过公共信道与下一跳节点通信以确定链路的信道分配;如果没有,则将感知到的各节点在每条信道上的干扰值Δk(c)利用文献[13]中的CMAODV路由协议进行路由发现。

从而可以看出,一条链路成功传输的概率不仅依靠接收端,同样也会受到发送端路径选择的影响。但从式(4)可以看出一条链路成功传输的比特概率与接收端的SNR有关,所以定义链路(i,j)的成功传输概率为

从式(2)~式(5)中可知,链路是否能够成功传输依赖于信道的分配。定义一个链路流量需求矩阵,记为F,其中包含了WMN网络中各条数据流从其源节点到目的节点所经过链路的流量需求,如fab(fab∈F)为一条链路的流量需求,则表示从节点a到节点b的链路的流量需求。令pathab为节点a到节点b的路径,则对于所需要构建的效用函数而言,效用函数的策略集S就是网络的可用正交信道,那么效用函数U(s)的物理意义则可以定义为:在给定流量需求矩阵F的情况下,能成功传输的流量。其表达式为
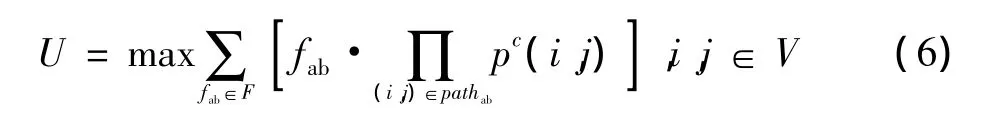
效用函数的目标就是最大化WMN网络的吞吐量。
1.3 收敛性
定义1(纳什均衡)[14]:如果策略s∈S是一个纳什均衡点,当且仅当对于每一个博弈者i,∀si(δ)∈i的策略空间,都满足

GBCA的纳什均衡意味着网络中没有弈者可以通过单独改变自身的策略使得效用函数U(s)得到改进。
定理1(纳什定理)[14]:每一个有限策略式博弈有一个混合策略或纯策略纳什均衡点。
具体证明请参照文献[14]中的证明。从定理1可以看出,GBCA算法至少存在一个纳什均衡点,在下一部分将会进行具体证明。
1.4 算法执行过程
为了使得网络中的吞吐量最大化,采用GBCA算法的WMN网络中的每一个节点都试图最小化网络的总干扰。这样每一个节点的信道分配问题就可以被视为一个联合博弈。弈者为每个节点,而信道则是每个弈者的可选策略。在GBCA中,每个弈者都存有一个如表1所示的状态表。表中的αi为数据流的目的节点,βi为数据流的下一跳节点(如果没有则进行路由发现),ci为所分配的信道。

表1 节点状态信息表
在GBCA中,每个弈者都使用整个网络的效用函数作为自己的效用,这是一种协同博弈,由于弈者的目标相同,所以GBCA算法的收敛速度要快于传统的博弈信道分配算法。可以看出,GBCA是一个重复博弈,在每次循环中弈者通过s-i来选择自身的策略以达到改善U(s)的目的。但是为了防止网络中的震荡,每个循环中只有一个弈者可以做出改变。因此,每个节点还包含有一个二进制表,此表标示出了该节点的行动次序。此外,还包含一个用于计数的标志K,标示还有几个节点可以通过改变自身策略以改善效用函数。在开始阶段,由于每个弈者都是随机采用的策略,所以可以改变策略使得效用函数得以改善,所以K=N。
GBCA的执行过程可以分为以下几个阶段:
1)起始阶段:各个节点随机分配信道,并形成状态表,此时的策略记为s0。
2)改进阶段:各个节点依照自己在二进制顺序表中的顺序,依次改变自己的策略。如当轮到节点i选择策略时,首先感知邻近节点在各信道上对自身造成的干扰,然后通过公共信道发送干扰值到下一跳节点,下一跳节点通过感知干扰值以及发送端所测量得到的干扰值来计算概率。如果存在一个策略si(δ)使得U(s)得到改善,则令sk+1=si(δ),同时保持K,广播K值,进入下一轮循环;如果没有策略使得U(s)得到改善,则令K=K-1,并将K进行广播,停留在这一轮循环,让下一个节点选择策略。
3)结束阶段:当K的值减小到0时,则整个网络进入到收敛状态,也即最佳状态,各节点将保持自身的策略。
从GBCA算法的3阶段可以得到定理2和定理3。
定理2:GBCA算法至少存在一个可达到的纳什均衡点。
证明:假设K不能够在有限的循环次数中减小到0,那就意味着总是存在至少一个节点和一个策略si(δ)使得效用函数得到改善,从而使得效用函数无U(s)一直增加。但是由于可用策略是有限的,那么U(s)必然不会无限制地增加,因此假设不成立。
定理3:GBCA算法可以收敛至一个纳什均衡点。
证明:整个算法中K递减至0的过程就是GBCA的收敛过程,当K=0时,算法即收敛至博弈中的一个纳什均衡点。
2 仿真与分析
在仿真中评估了GBCA算法和文献[7]中的SICA算法的性能。20~50个网状节点随机分布在一个1000 m×1000 m范围内,其中有1~3个节点作为网关节点,无线网状网在设置中配置3条天线,且节点的传输半径为200 m,干扰半径为400 m。场景中有8条可用正交信道,其中一条信道设为公共信道用于传输公共数据包。随机将2~10条CBR数据流随机分配给网络中的节点,使用NS2.34作为仿真工具。
首先比较GBCA算法和SICA算法的收敛速度。图2展示的是在网络节点数为20个时,以丢包率来衡量的收敛性。从图2中可以看出GBCA算法的收敛速度要比SICA算法的收敛速度快,GBCA算法在循环了40次以后进入收敛状态,而SICA算法则是要执行69次循环后才进入收敛状态。这是因为GBCA算法的效用函数是针对全局最优的,而不是局部优化的。
图3显示了当网络节点数量为20时,不同数据流情况下GBCA算法和SICA算法的丢包率比较,可以看出GBCA算法的传输性能要高于SICA算法。因为在SICA算法中只有1个发送天线和1个接收天线,在传输时需要不停地切换信道来实现多条数据流的传输,一部分数据因信道切换时造成的扰动而丢失,并随着数据流的增加而不断增大。GBCA算法中存在多个天线,无需频繁切换信道,且能够将干扰小的信道分配给链路,以保证数据流的成功传输。


图4展示了网络中有7条数据流时丢包率和网络中节点数的关系,从图中可以看到GBCA算法的丢包率明显低于SICA算法的丢包率。同样是因为SICA算法只有两个天线随着节点数目的增多,需要切换信道的次数也随之增大,并且其算法中并没有重点优化网络数据流间的干扰,所以导致丢包率较高。

图4 不同Mesh节点数对丢包率的影响
图5和图6分别对两种算法在不同条件下的平均端到端时延进行了仿真分析。图5是从不同Mesh节点数目的情况下对两种算法的时延进行了分析,而图6则是对不同数据流的流量进行了分析。图5所示的仿真实验的设置为:网络中随机分配了7条数据流,数据流量为500 kbit/s。由图5可以看出SICA算法的端到端时延要略微低于GBCA算法,造成这种结果的原因是在于SICA算法不需要一条公共信道来进行公共信令的传输,从而省去了信令交换的时间。图6的仿真设置为网络中有20个节点,随机分配了7条数据流。图6表示在数据流流量较小时SICA算法的信道切换频率较低,切换所造成的时延也较小。但是随着数据流流量的增大,SICA算法的信道切换频率也随之增加,则造成了较高的切换时延。


图7所代表的仿真设置是当网络中有20个节点,其中有一个作为网关节点,并且有2~10条随机分布流量为1000 kbit/s的数据流。图7中给出了两种算法的吞吐量随着网络负载变化的情况,可以看出当负载较低时两种算法的网络吞吐相差不大。但是随着网络负载的增加,GBCA算法的网络吞吐量逐渐优于SICA算法,这是因为GBCA算法是采用全局最优的方法,使得整个网络的吞吐量最大化。

3 总结
众所周知,WMN网络中的信道分配问题一直是一个NP难的问题,本文根据无线Mesh网络分布式的特点,引入博弈论方法来解决这个问题,将问题模型化为整个网络的联合博弈。并提出了GBCA算法,算法执行过程中通过公共信道传输公共信令包,使得收发节点协同选择出使得效用函数最大的策略,最终达到最大化网络吞吐量的目标。
在文中给出了GBCA算法的具体实现,并且证明了算法的收敛性。本文通过NS2仿真工具,将GBCA算法和SICA算法进行了比较,结果表明GBCA算法有更快的收敛速度、较低的丢包率、较低的端到端时延以及比较大的网络吞吐量等特点。
[1]方旭明.下一代无线英特网技术:无线Mesh网络[M].北京:人民邮电出版社,2006.
[2]AKYILDIZ I,WANG X.A survey on wireless mesh networks[J].IEEE Communications Magazine,2005,43(9):23-30.
[3]KODIALAM M,NANDAGOPAI T.The effect of interference on the capacity of multi-hop wireless networks[C]//Proc.IEEE Symposium on Information Theory.Chicago,USA:IEEE Press,2004:470-479.
[4]BRUNO R,CONTI M,GREGORI E.Mesh networks:commodity multihop ad hoc networks[J].IEEE Communications Magazine,2005,43(3):123-131.
[5]陈美飞,赵新建.无线Mesh网络安全路由算法研究[J].电视技术,2009,33(S1):116-118.
[6]DRAVES R,PADHYE J,ZILL B.Routing in multi-radio,multi-hop wireless mesh network[C]//Proc.ACM l0th Annual International Conference10th Mobile Computing and Networking.Pennsylvania,USA:ACM Press,2004:114-128.
[7]RANIWALA A,GOPALAN K,CHIUEH T.Centralized channel assignment and routing algorithms for multi-channel wireless mesh networks[J].ACM SIGMOBILE Mobile Computing and Communications Reviews,2004,8(2):50-65.
[8]REN J,QIU Z D.Centralized quasi-static channel assignment in multi-radio wireless mesh networks[C]//Proc.IEEE International Conference on Communications Systems.Guangzhou,China:IEEE Press,2008:1149-1154.
[9]REN J,QIU Z D.Centralized quasi-static channel assignment for multiradio wireless mesh networks[J].Wireless Sensor Network,2009(2):104-111.
[10]SUBRAMANIAN A P,GUPTA H,DAS S R.Minimum-interference channel assignment in multi-radio wireless mesh networks[C]//Proc.4th Annual IEEE Communications Society Conference on Sensor mesh and Ad Hoc Communications and Networks.California,USA:IEEE Press,2007:481-490.
[11]MARYAM A N,LLORENC C A.Adaptive channel assignment for wireless Mesh networks using game theory[C]//Proc.8th IEEE International Conference on Mobile Ad-Hoc and Sensor Systems.[S.l.]:IEEE Press,2011:746-751.
[12]BLOUGH D,RESTA G,SANTI P.Approximation algorithms for wireless link scheduling with SINR-based interference[J].IEEE/ACM Trans.Networking,2010,18(6):1701-1712.
[13]吴涛.基于跨层设计的无线Mesh网络资源分配与QoS优化研究[D].重庆:重庆邮电大学,2011.
[14]MACKENZIE A B,DASILVA L A.Game theory for wireless engineers[M].New York:Morgan and Claypool,2006.

