道路交通事故预测模型的研究

姬利娜 宋清华

(安阳工学院，河南 安阳 455000)

道路交通事故几乎每天都会发生，由于其危害性极大，备受人们关注。交通事故预测可以根据以往发生事故的变化规律，对未来的不确定的事故作出推理，从而为制定交通安全对策提供理论依据。

1 交通事故预测模型的分析构建

1.1 线性回归预测模型

在许多实际问题中，影响城市道路交通事故的因素往往不只一个而常常是多个，称此类回归问题为多元回归。线性回归预测多数是利用多元线性回归方程，通过寻找与因变量具有较强关联关系的因素作为自变量，计算回归系数，并经过相关分析和显著性检验后，最终确定回归预测方程。其一般形式如下:

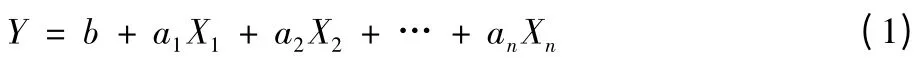
式中:b，a1，a2，an为回归系数。目前较典型的线性回归预测模型有两种:伊·阿拉加尔模型和北京模型。

1.2 非线性回归预测模型

驾驶员的人为失误可能导致交通事故，为便于定量描述人为失误对交通事故的影响，采用人为失误率预计法［1］(THERP 法)，得出驾驶员总的操作失误率P总、人为失误率P与事故发生总量Y 之间的关系。参照Logistic 的建模思想，建立模型为y = k/(1 + ae-bp)(k，a，b 为待识别参数，且均大于0)。通过公式转换，可得:

1.3 灰色预测模型

GM(1，1)模型是最常用的一种灰色模型，其一般形式为:x(0)(k)+x(1)(k)= μ，参数辨识过程如下:

(1)构造数据矩阵B

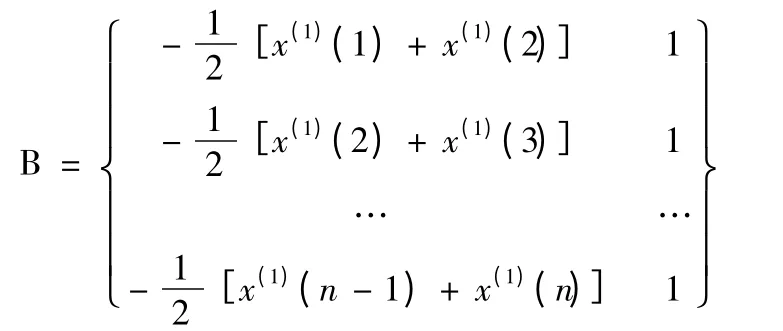
(2)构造数阵向量yn=［x(0)(2)，x(0)(3)，…，x(0)(n)］T

通过还原处理得到预测值后，还需对预测模型进行检验。本文介绍GM(1，1)模型精度检验常用的两种方法:残差检验和后验差检验。

①残差大小检验。残差E(t)= R(1)(t)-(1)(t)，相对残差

②后验差检验。设原始数列R 与残差数列E 的平均值分别为和。

记原始数列和残差数列的均方差分别为S1和S2，然后定义后验差比值，小误差频率P = P{︱E(t)-︱ ＜0.6745 S1}

按P与C的大小，可将预测精度分为好、合格、勉强、不合格四类，详见表1。

表1 P、C 值预测精度

2 道路交通事故灰色预测实例应用

本文选择云南省某市2000～2005年道路交通事故次数和死亡人数进行灰色预测。表2 反映了该市道路交通事故次数(R)和死亡人数(S)的原始数据情况，这里以R 为例演示灰色预测方法的运用，据此预测2013～2015年的交通事故发生情况。

表2 交通事故次数和死亡人数统计表

(1)交通事故次数原始数据

(2)原始数据一次累加生成

(3)参数向量计算

(4)预测模型建立

(5)模型精度检验

a.残差检验

进行残差检验后，模型的相对误差(见表3)不是很大，模型的精度也较好。

表3 事故次数R 预测值的残差E(t)及相对残差e(t)

b.后验差检验

经计算得后验误差比值C =0.2958，小误差频率P =1。根据灰色预测精度等级判断标准(见表1)知，所建立的道路交通事故灰色预测模型精度较好，可以用于事故预测。

(6)事故预测

运用所建立的灰色预测模型预测2013～2015 事故次数分别为:2044，2998，3568。同样可以按照上述分析流程对该市的交通事故死亡人数进行预测，预测结果见表4。

表4 GM(1，1)预测模型计算结果一览表

3 结束语

通过对建立的灰色预测GM(1，1)模型进行精度检验，可见，运用灰色理论进行道路交通事故预测是可靠的。以上三种模型对交通事故预测侧重于不同方面，灰色预测能在原始数据分布波动大、样本少时，能相对较准确地预测未来交通事故的发展趋势，以达到减少交通事故的目的。

［1］刘建齐.道路交通事故预测中的灰色预测模型［J］.广西交通科技，2003，28(4):100—109.

［2］过秀成.道路交通安全学［M］.南京:东南大学出版社，2001.

［3］成卫，张瑾，李学敏著.城市道路交通安全理论模型与方法.云南人民科技出版社:2005.

［4］郑建湖，黄明芳，陈慧.福州市道路交通事故灰色预测模型的构建与实现［J］.武汉理工大学学报(交通科学与工程版)，2011，(03)