映射变换方法在数学分析中的应用

高婷婷，张明会

（陇南师范高等专科学校 数学系，成县742500）

1 数学变换方法的特征概述

所谓数学变换方法，概括地讲，就是在解决数学问题时，采用迂回的方式和“改头换面”的手段来达到目的的一种方法.具体地讲，就是在研究或解答数学问题时，将复杂的问题通过适当的变换转化成简单的问题，将繁难的问题通过适当的变换转换成容易的问题，从而达到解决问题的目的.

从思维特征看：数学变换方法不是“守株待兔”，而是主张在运动、变化中去寻求问题的答案.这就是所谓的动态思维.

从方法的特征看：数学变换方法的主要特征是灵活、多样，即对同一个数学结构，其变形方式并非唯一，而是多方位的，可以通过各种可能的途径去求得问题的解决.正因为这种多样性，就给人们解决问题提供了很大的自由度.

从数学结构的内在规律性看：数学结构组成元素之间的互相依存和联结的形式具有可变性，人们正是利用了这种可变性的特征，来强化自身在解决数学问题时的应变能力，而不断地提高自己解决数学问题的技能和技巧.

虽然用变换的方法解决数学问题形式多样、方法灵活，但已解决问题过程的整体逻辑结构框架来看，却有其相同和相似之处.因此，在介绍用变换方法解决具体问题之前，有必要指出它们的共性，即变换方法应用中都具有如下相同的思路结构框架：

从以上变换方法的逻辑结构框架可以看出，要用变换方法解决数学问题，关键在于寻找变换T与其逆变换T－1的表达式，这就为人们提出了两个尚待探讨的问题：一是对每一个数学问题都能通过某种变换方法得到解决.这就表明，变换方法尽管灵活且应用广泛，但并非万能.二是如果这样的变换存在，如何具体地找出来？一般地讲，这既非变换方法本身所能解决，也非全靠逻辑思维所能办到，主要靠高度的想象力和洞察力去进行探索性的发现.

2 映射变换

用集合与对应的观点看，映射就是在两个集合元素之间建立的一种特殊的对应关系.映射变换的主要特点是：灵活性强，覆盖面广.利用映射变换解决问题的思路结构框架是：

从现代数学的观点看，数学分析中的函数关系，就是由实数集到实数集的特殊映射.下面举例说明映射变换方法在数学分析中的一些具体应用.

例1 定积分的换元公式

设f在区间（a，b）上连续，函数x＝φ（t）足条件：

①将区间（α，β）变为区间（a，b），且φ（α）＝a，φ（β）＝b；

②在（α，β）上有连续导数φ′（t）；则

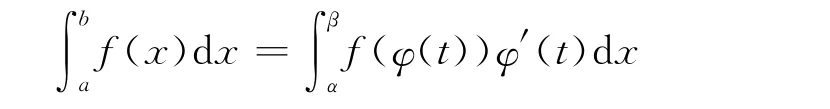
例2 在二重积分的计算中，极坐标变换为

其逆变换为：

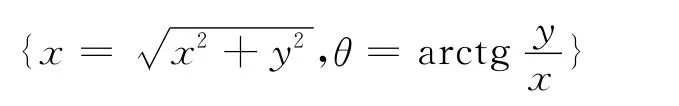
此变换极为有用，二重积分极坐标变换公式为：

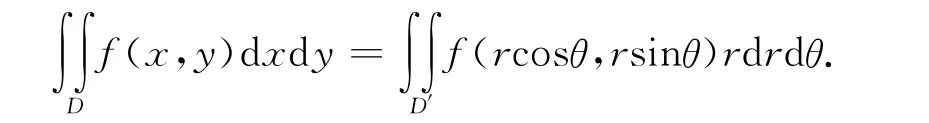
在三重积分的计算中，柱坐标与球坐标变换经常使用，点P 的直角坐标（x，y，z）与柱坐标（r，θ，z）有变换式；

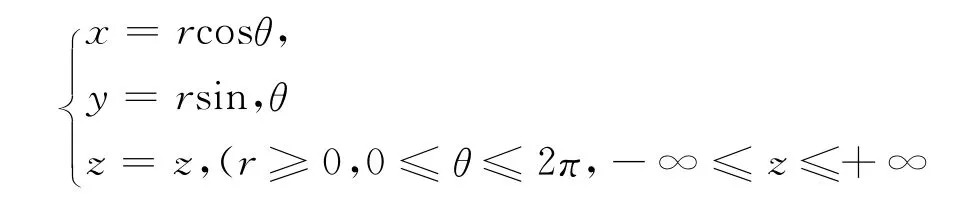
三重积分的柱坐标变换公式是：

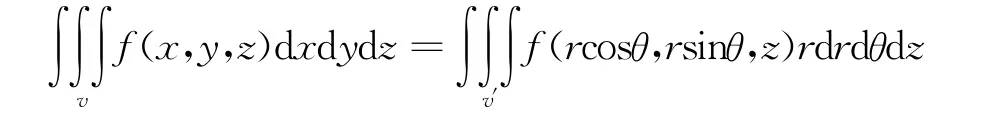
点P的直角坐标 （x，y，x）与球坐标（ρ，φ，θ）的变换式为

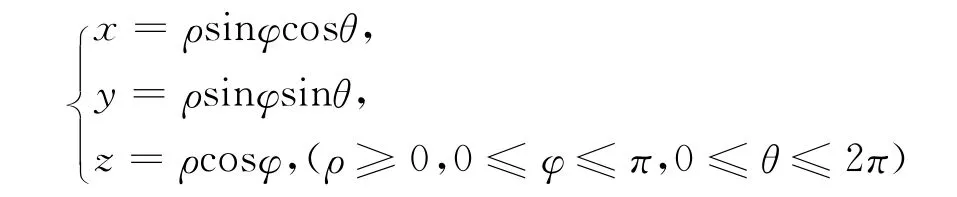
三重积分的球坐标变换式为：

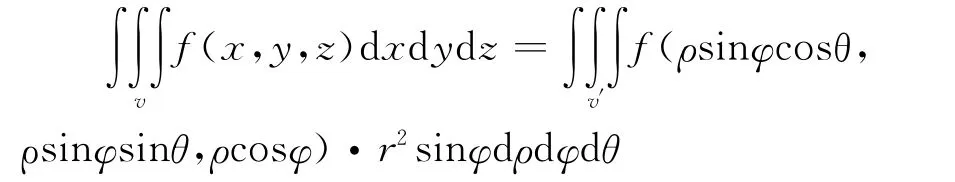
例3 在求某些幂级数的和函数时，采用映射变换的方法往往很有效，例如

10求幂级数

的和函数

解 设和函数为f（x），取微分算子D作为映射，即

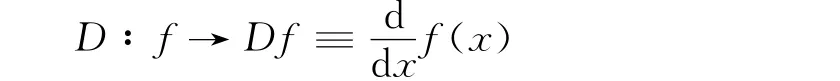
于是有

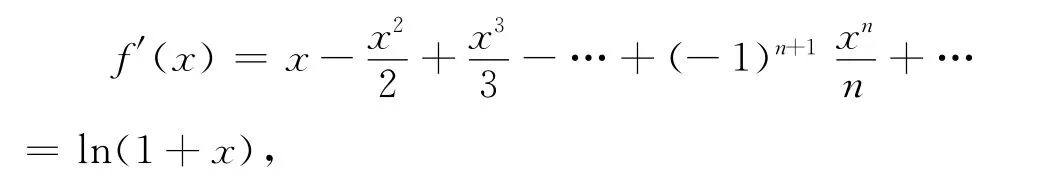
对上式两边积分得

从而有

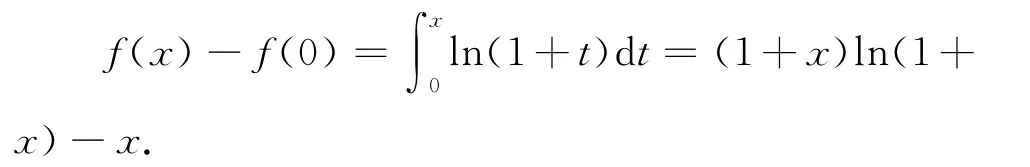
又因f（0）＝0，故有

f（x）＝ （1＋x）ln（1＋x）－x 20求冥级数

1·2＋2·3x＋3·4x2＋…＋（n＋1）（n＋2）xn＋…的和函数

解 取积分算子∫作为映射，即

于是有

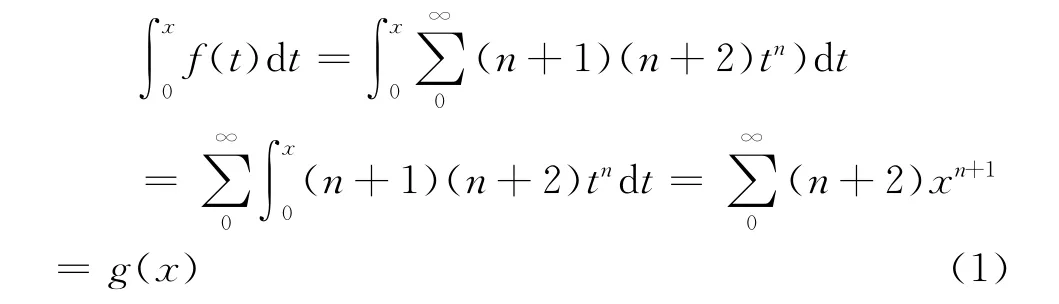
再对g（x）作一次积分映射，即

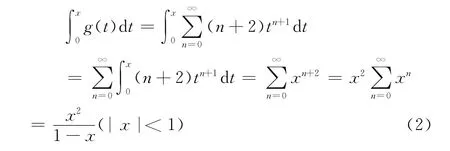
对（2）式两边求导，得

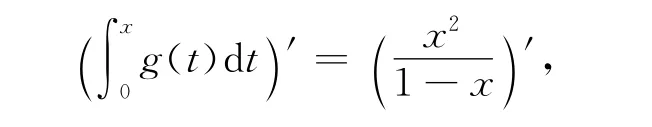
从而有

将（3）式代入（1）式有

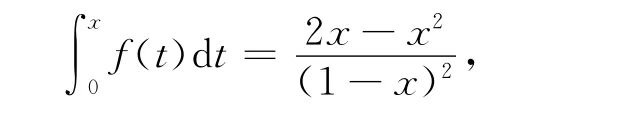
对上式再两边求导，即得原级数的表达式.

［1］ 华东师范大学数学系.数学分析（第三版）［M］.北京：高等教育出版社，2001.

［2］ 马振华.离散数学导引［M］.北京：清华大学出版社，2006.

［3］ 裴礼文.数学分析中的典型问题与方法［M］.北京：高等教育出版社，2002.

［4］ 马振民，吕克璞.微积分习题类型分析［M］.兰州大学出版社，1999.

［5］ 张明会.恒等变换方法在数学分析中的应用［J］.湖南工程学院学报，2011（2）.