钢筋混凝土梁的弯曲性能尺寸效应试验研究
车 轶,陈志鑫,2,宋玉普,黄治宇,3
(1.大连理工大学 建设工程学部,辽宁 大连116024;2.大连城建设计研究院有限公司,辽宁 大连116021;3.大连民族学院 土木建筑工程学院,辽宁 大连116600)
研究表明,混凝土作为一种准脆性材料的力学性能存在尺寸效应,相应地混凝土构件的一些力学和变形性能也存在尺寸效应,因此在某些特定的情况下根据小尺寸试件试验结果建立的构件性能计算方法应用到大尺寸构件设计时,往往不够准确也不科学[1-4]。近年来,各国学者对无腹筋和配置少量箍筋混凝土梁,以及厚板等构件的受剪承载力尺寸效应进行了较深入的研究,并取得了较大进展[5-8]。相比之下,人们对钢筋混凝土构件受弯性能尺寸效应研究相对较少,并且得出的结论尚不统一。
对于受弯承载力,多数研究认为不存在明显的尺寸效应[9-11],但少数研究者[12-13]认为存在尺寸效应;而对于位移延性和塑性铰区转动能力,大部分研究表明试件的尺寸效应很明显[14-17],但 Alca等[9]的研究认为无明显尺寸效应。车轶等[18]采用中间带有短柱的梁式试件模拟框架梁梁端的受力特征,进行了梁高250~1 000mm的高强混凝土(C70)梁的弯曲性能试验。试验研究结果表明,截面高度对构件的名义开裂弯矩、名义屈服弯矩和名义极限弯矩没有明显影响,而构件的位移延性系数和塑性铰的塑性转角则存在明显的尺寸效应。
文章在文献[18]研究基础上,进一步开展了普通混凝土梁的弯曲性能尺寸效应试验研究。根据本文和文献[18]的试验结果,分析了截面高度对钢筋混凝土构件的受弯力学特性(开裂弯矩、屈服弯矩、极限弯矩)和变形能力(位移延性、塑性转动能力)的影响。
1 试验概况
除混凝土强度外,试件形式与参数与文献[18]相同。试件形式和具体几何参数分别见图1和表1,其中b、h分别为截面宽度和高度,h0为截面有效高度,a为计算长度,ρs、ρ′s和ρsv分别为受拉、受压纵筋和箍筋的配筋率。试件截面尺寸分别为1 0 0mm×2 5 0mm、2 0 0mm×5 0 0mm,3 0 0mm×750mm和400mm×1 000mm,截面高宽比和剪跨比分别为b/h=1∶2.5和a/h0=3.5。所有试件的受拉纵筋配筋率均为1.08%,在混凝土设计规范[19]规定的适筋梁范围内,配箍率为0.52%,受压纵筋配筋率分为两种,分别为1.08%和0.69%。
采用C40普通商品混凝土浇筑试件,同时每个试件预留3个混凝土标准试块,与试件同条件养护,试件试验前进行立方体试件强度试验,确定试件混凝土强度fcu。纵筋采用HRB400级钢筋,箍筋采用HPB235级钢筋。混凝土组分用量及钢筋力学性能分别见表2和表3。试件配筋及混凝土强度实测值见表1。

表1 试件参数

表2 混凝土各组分用量
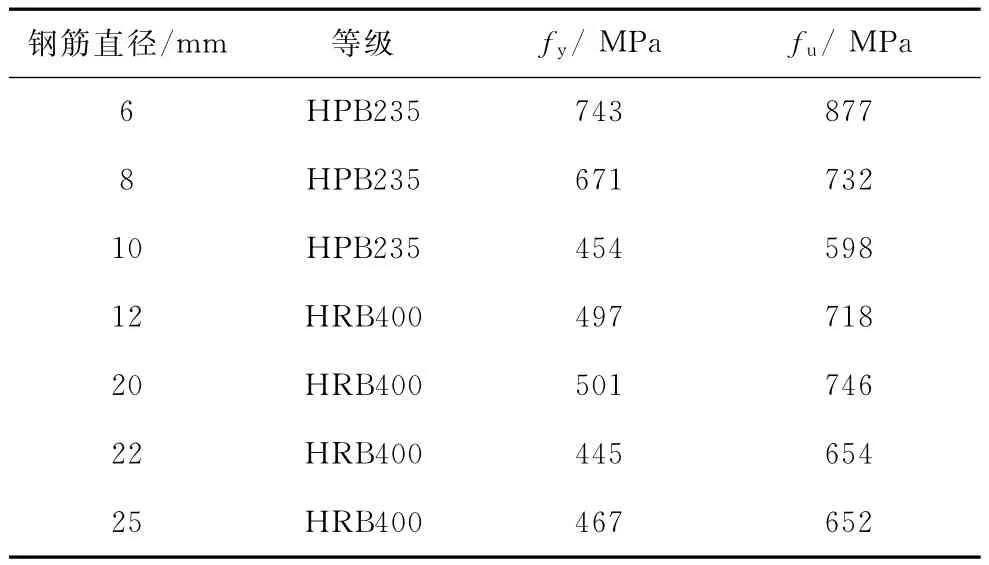
表3 钢筋力学性能
试验加载装置如图2所示。千斤顶作用于试件中部短柱处施加竖向荷载,并用荷载传感器测量荷载值。在梁端和支座处布置电子位移计和LVDT测量试件的挠度,纵筋和箍筋主要位置处布置电阻应变片测量钢筋应变,梁端顶部布置混凝土应变片以测量混凝土压应变。试验加载程序参照《混凝土结构试验方法标准》[20]进行。

图2 加载装置
2 试验现象与试验结果
2.1 试验现象与荷载 挠度曲线
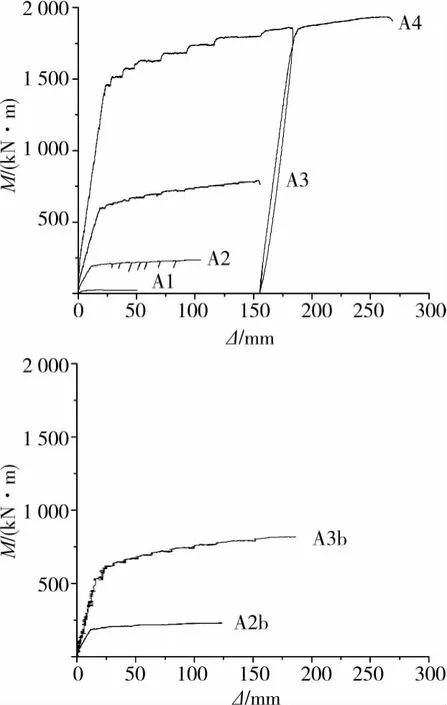
图3 试件的弯矩 挠度曲线
图3为各试件的弯矩 挠度曲线。各试件由加载至最终破坏的过程大体相近。在开裂之前,曲线为直线,试件处于线弹性阶段;开裂之后,构件刚度有所下降,曲线斜率增大;当达到屈服荷载时,曲线出现明显的拐点,挠度增加较快;当受压区混凝土出现明显的压碎现象时,荷载迅速下降,试件破坏。以试件A4为例,加载至122.2kN时,短柱左右两侧梁端出现竖向弯曲裂缝,两侧裂缝位置和高度基本对称。加载至909.1kN时,受拉纵筋屈服,弯矩 挠度曲线出现明显拐点,此时短柱左侧梁的主要裂缝发展至距梁顶约150mm处,右侧发展至约200mm处,此外在主裂缝附近还出现许多短斜裂缝,最大裂缝宽度为0.34mm。在这一级荷载阶段,短柱左侧梁端压区保护层混凝土出现水平裂缝,加载至945.9kN·m时,短柱右侧梁也出现水平裂缝。加载至1 166.8kN时,靠近梁端的主要裂缝斜向延伸至梁端顶部,最大裂缝宽度大于3mm,梁顶混凝土出现明显的压碎迹象,试件破坏。各试件的破坏形态和裂缝分布图4,破坏时各试件短柱两侧在的裂缝形态基本对称。
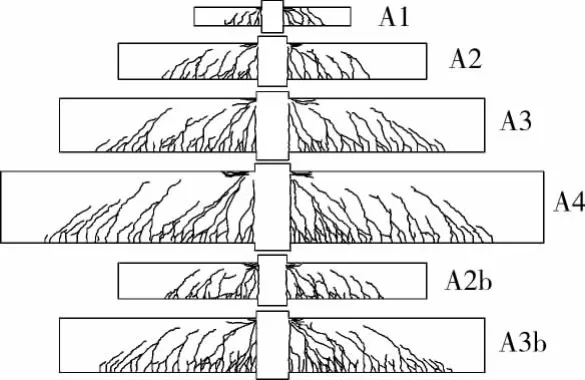
图4 各试件裂缝形态
2.2 试验结果
各试件的开裂、屈服和极限弯矩,以及相应的位移试验结果见表4。混凝土受拉区内出现第一条弯曲裂缝时的弯矩为开裂弯矩;最大弯矩截面纵向受拉钢筋应变达到屈服应变时的弯矩为构件的屈服弯矩;当梁顶受压区混凝土出现破碎时,认为试件发生最终破坏,此时的弯矩为极限弯矩。
各试件的塑性铰区长度可根据受拉纵筋上的应变测量结果确定。表5给出各试件梁端塑性铰区长度lp试验结果。由结果可得,塑性铰区长度lp约为1倍的截面有效高度。文献[18]的试验结果表明,高强混凝土梁的塑性铰区长度为0.95~1.15h0,与文章结论十分接近,由此可见混凝土强度对梁的塑性铰区长度没有明显影响。

表4 试件试验结果
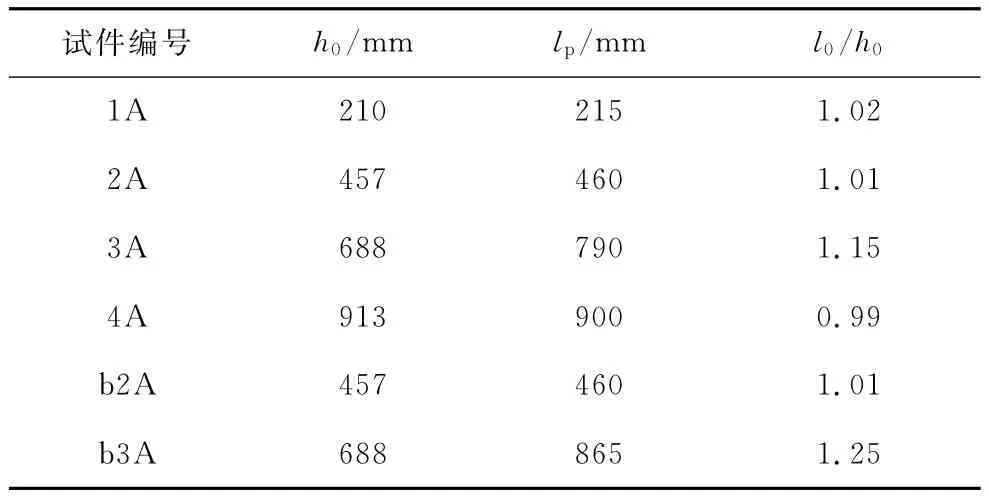
表5 梁端塑性铰区长度实测结果
3 截面高度对弯曲性能影响
3.1 名义受弯承载力
为了考察试件截面高度对受弯承载力的影响,试件的开裂弯矩Mcr、屈服弯矩My和极限弯矩Mu分别用名义弯矩Mcr/bh02、My/bh02和 Mu/bh02表示,并绘于图5。图中还同时给出了文献[18]的试验结果,以便比较混凝土强度的影响。可以看出,文中试件与文献[18]试件的开裂弯矩、屈服弯矩和极限弯矩均未表现出明显的尺寸效应。
相同尺寸和配筋条件下,文中试件的开裂弯矩明显小于文献[18]中高强混凝土试件的开裂弯矩,而相应的屈服弯矩和极限弯矩则相差不大。原因是开裂弯矩主要由混凝土抗拉强度控制,屈服和极限弯矩则主要与纵向钢筋强度有关,文献[18]中高强混凝土试件的混凝土强度为72.1~72.4MPa,明显高于文中试件,而纵向钢筋的屈服强度相差不大。
3.2 位移延性
构件的变形能力可用位移延性系数μ来描述,由下式计算:
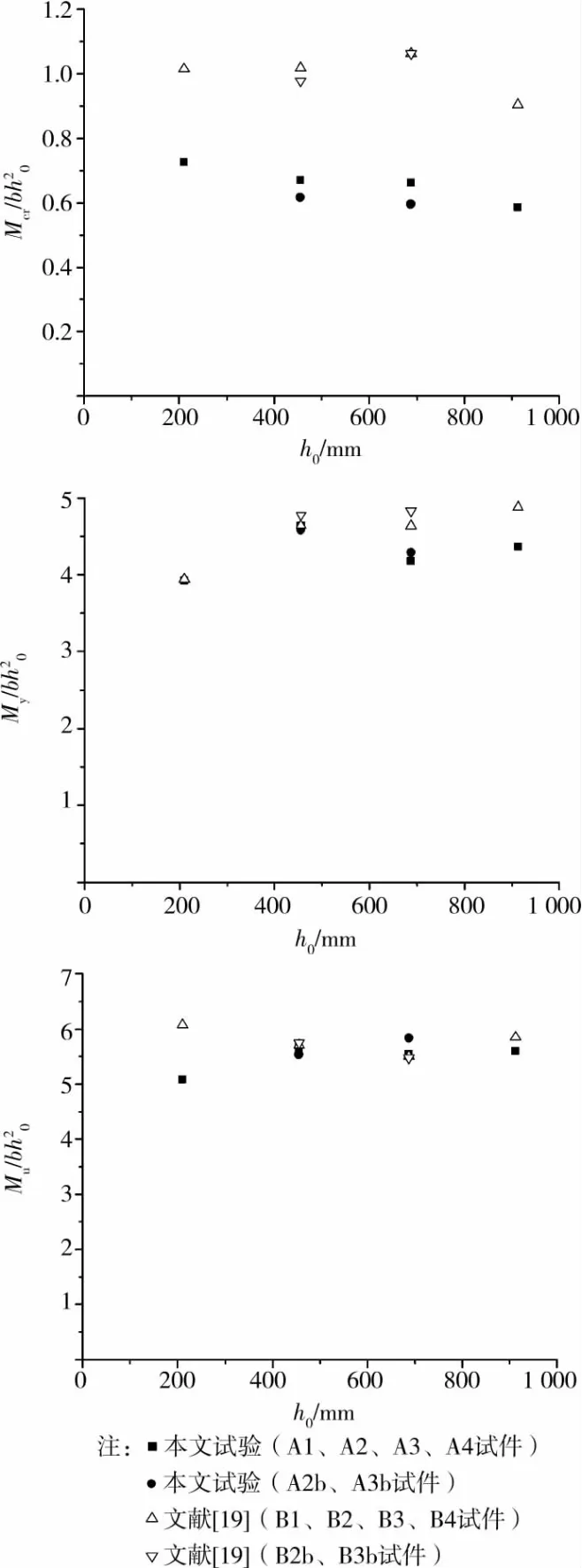
图5 梁高对试件名义弯矩随梁高的影响

式中:Δu、Δy分别为极限荷载和屈服荷载下的竖向极限位移和屈服位移。
图6同时给出了本文和文献[18]中各试件的位移延性系数结果随梁高变化情况。由图可见,本文和文献[18]各试件的位移延性系数均随试件高度增加有明显下降趋势,并且二者下降规律相近。因此可以认为钢筋混凝土适筋梁的位移延性系数存在明显的尺寸效应,随梁高的增加而减小,并且这种减小规律不受混凝土强度影响。
对比文献[18]的试验结果可以发现,其他参数相同的情况下,混凝土强度低的试件位移延性系数较高,主要原因是尽管文中试件与文献[18]试件配筋相同,但文中试件的箍筋屈服强度实测值要明显高于文献[18]试件,临近构件破坏时对梁端受压区混凝土的约束能力更强,有利于提高构件的延性。此外,由文章的试验结果还可以发现,纵向受压钢筋配筋率较低的试件A2b和A3b的延性系数分别为试件A2和A3的93%和92%,说明增加受压钢筋配筋率可提高构件的延性。
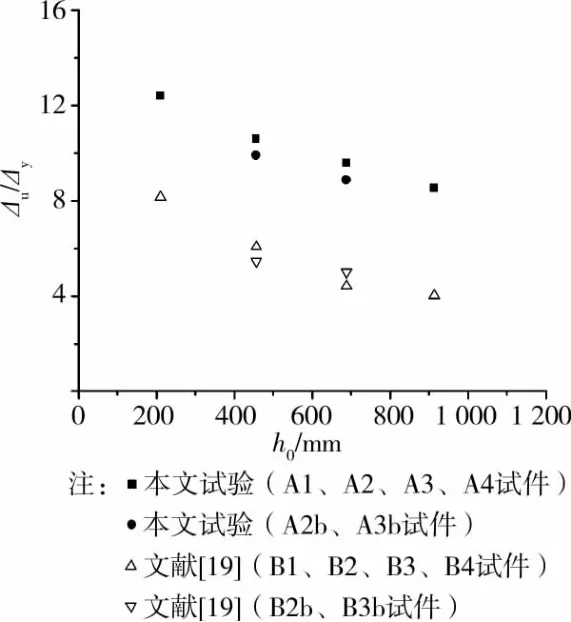
图6 梁高对试件延性系数随梁高的影响
3.3 塑性铰转角
塑性铰区的塑性转动能力是描述钢筋混凝土构件弹塑性变形能力的重要参数。由于试验中直接测量塑性铰区的转动能力难度较大,文章利用挠度测量结果间接确定试件的塑性铰区塑性转角。由于纵向受拉钢筋屈服后,试件的竖向变形主要集中在塑性铰区,塑性铰区以外区域的变形相对较小,因此,可以利用试件挠度试验结果计算塑性铰区的塑性转角:

式中:θu、θy分别为极限荷载和屈服荷载时的塑性铰区两端截面的相对转角;Δu、Δy分别为极限荷载和屈服荷载时的梁端极限位移和屈服位移;a为梁端到支座处距离。
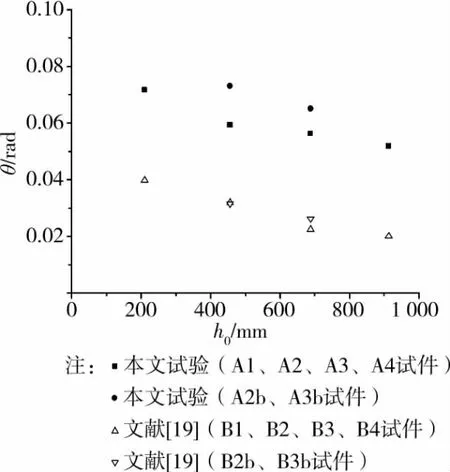
图7 梁高对塑性铰转动能力的影响
图7为此文和文献[18]试件的试验结果。可以看出,文中的普通混凝土试件和文献[18]的高强混凝土试件的塑性铰转角均表现出明显的尺寸效应,塑性转角随梁高的增大而减小,并且相同条件下普通混凝土和高强混凝土试件的塑性转动能力随截面高度的下降趋势大体相同。
4 结 论
文章进行了强度为46.5~50.6MPa的混凝土试件弯曲性能尺寸效应试验研究,并与文献[18]中相同尺寸和配筋的高强混凝土试件的试验结果进行了对比分析,得出结论如下:
1)对于混凝土试件的弯曲性能是否存在尺寸效应问题,文章试验结论与高强混凝土试验结论一致,即试件的名义开裂弯矩、屈服弯矩和极限弯矩不存在明显的尺寸效应,即不受截面高度影响;试件的变形指标,如位移延性系数和塑性铰区的塑性转动能力则存在明显尺寸效应,随截面高度的增加而减小,并且普通混凝土和高强混凝土试件的位移延性系数和强度尺寸效应规律大致相同。
2)其他参数相同的情况下,混凝土强度低的试件位移延性系数较高,原因是文中试件的箍筋屈服强度实测值要明显高于文献[18]试件,对梁端受压区混凝土的约束更强,有利于提高构件的延性。
3)文章和文献[18]的试验结果均表明,混凝土试件的塑性铰区长度约为1倍的截面有效高度。
[1]Bazant Z P,Ozbolt J,Eligehausen R.Fracture size effect:Review of evidence for concrete structures [J].Journal of Structural Engineering,1994,120(8):2377-2398.
[2]Bazant Z P,Gettu R,Jirasek M,et al.Quasibrittle fracture scaling and size effect-Final report [J].Materials and Structures,2004,37:547-568.
[3]Viso J R D,Carmona J R,Ruiz G.Shape and size effects on the compressive strength of high-strength concrete[J].Cement and Concrete Research,2008,38:386-395.
[4]杜修力,张建伟,符佳,等.钢筋混凝土构件的尺寸效应研究进展及展望[J].建筑科学与工程学报,2009,26(3):14-18.Du X L,Zhang J W,Fu J,et al.Research progress and prospect of size effect on reinforced concrete members [J].Journal of Architecture and Civil Engineering,2009,26(3):14-18.
[5]Shioya T,Iguro M,Nojiri Y,et a1.Shear strength of large reinforced concrete beams[C]//Livc,Bazant Z P.Fracture Mechanics:Applications to Concrete.Detroit:ACI,1989:259-279.
[6]Che Y,Yu L,Song Y P.Shear strength of reinforced concrete beams without web reinforcement[C]//Advances and Trends in Structural Engineering,Mechanics and Computation.London,UK:CRC Press,2010:195.
[7]Collins M P,Kuchma D.How safe are our large,lightly reinforced concrete beams,slabs,and footings?[J].ACI Structural Journal,1999,96(4):482-490.
[8]Yu Q,Bazant Z P.Can stirrups suppress size effect on shear strength of RC beams?[J].Journal of Structural Engineering,2011,137(5):607-617.
[9]Alca N,Alexander S D B,Macgregor J G.Effect of size on flexural behavior of high-strength concrete beams [J].ACI Structural Journal,1997,94(1):59-67.
[10]Ozbolt J,Mestrovic D,Li Y J,et al.Compression failure of beams made of different concrete types and sizes[J].Journal of Structural Engineering,2000,126(2):200-209.
[11]Corley G W.Rotational capacity of reinforced concrete beams[J].Journal of the Structural Division,ASCE,1966,92(5):121-146.
[12]Appa R G,Vijayanand I,Eligehausen R.Studies on ductility and evaluation of minimum flexural reinforcement in RC beams[J].Materials and Structures 2008,41(4):759-771.
[13]Belgin C M,Sener S.Size effect on failure of over reinforced concrete beams[J].Engineering Fracture Mechanics,2008,75:2308-2319.
[14]Carpinteri A,Corrado M,Paggi M,et al.New model for the analysis of size-scale effects on the ductility of reinforced concrete elements in bending [J].Journal of Engineering Mechanics,2009,135(3):221-229.
[15]Hillerborg A.Rotational capacity of reinforced concrete beams[J].Norwegian Concrete Research,1988,7:121-134.
[16]Bigaj A J,Walraven J C.Size effect on rotational capacity of plastic hinges in reinforced concrete beams [J].CEB Bulletin d'Information,1993,218:7-23.
[17]Bigaj A J,Walraven J C.Size effects in plastic hinges of reinforced concrete members[J].Heron,2002,47(1):53-75.
[18]车轶,郑新丰,王金金,等.单调荷载作用下高强混凝土梁弯曲性能尺寸效应研究[J].建筑结构学报,2012,33(6):96-102.Che Y,Zheng X F,Wang J J,et al.Size effect on flexural behavior of reinforced high-strength concrete beams subjected to monotonic loading[J].Journal of Building Structures,2012,33(6):96-102.
[19]GB 50010-2010混凝土结构设计规范[S].北京:中国建筑工业出版社,2010.
[20]GB 50152-92混凝土结构试验方法标准[S].北京:中国建筑工业出版社,1992.

