Principal Quasi-Baerness of Rings of Skew Generalized Power Series

ZHANG WAN-RU

(Department of Mathematics,Hexi University,Zhangye,Gansu,734000)

Communicated by Du Xian-kun

Principal Quasi-Baerness of Rings of Skew Generalized Power Series

ZHANG WAN-RU

(Department of Mathematics,Hexi University,Zhangye,Gansu,734000)

Communicated by Du Xian-kun

Let R be a ring and(S,≤)be a strictly totally ordered monoid satisfying that 0≤s for all s∈S.It is shown that if λ is a weakly rigid homomorphism,then the skew generalized power series ring[[RS,≤,λ]]is right p.q.-Baer if and only if R is right p.q.-Baer and any S-indexed subset of Sr(R)has a generalized join in Sr(R). Several known results follow as consequences of our results.

rings of skew generalized power series,right p.q.-Baer ring,weakly rigid endomorphism

1 Introduction

Throughout this paper,R denotes an associative ring with unity.Recall that R is(quasi-) Baer if the right annihilator of every nonempty subset(every right ideal)of R is generated by an idempotent.In[1]Kaplansky introduced Baer rings to abstract various properties of AW*-algebras and Von Neumann algebras.Clark defined quasi-Baer rings in[2]and used them to characterize when a finite dimensional algebra with unity over an algebraically closed field is isomorphic to a twisted matrix units semigroup algebra.Further work on Baer and quasi-Baer rings appears in[3–6].As a generalization of quasi-Baer rings,Birkenmeier, Kim and Park in[7]introduced the concept of principally quasi-Baer rings.A ring R is called right principally quasi-Baer(or simply right p.q.-Baer)if the right annihilator of every principal right ideal of R is generated by an idempotent.Similarly,left p.q.-Baer rings can be defined.A ring is called p.q.-Baer if it is both right and left p.q.-Baer.For more details and examples of right p.q.-Baer rings,see[8–13].

It was proved that a ring R is quasi-Baer if and only if R[X]is quasi-Baer if and onlyif R[[X]]is quasi-Baer,where X is an arbitrary nonempty set of not necessarily commuting indeterminates(see[3],Theorem 1.8).Birkenmeier et al.[8]showed that R is right p.q.-Baer if and only if R[x]is right p.q.-Baer(see[8],Theorem 2.1),and an example([8],Example 2.6)was given to show that the result is not true for R[[x]].In[10],a necessary and sufficient condition was given for some rings under which the ring R[[x]]is right p.q.-Baer (see[10],Theorem 3).It is shown that for a ring R with Sℓ(R)⊆C(R),R[[x]]is right p.q.-Baer if and only if R is right p.q.-Baer and any countable family of idempotents in R has a generalized join in I(R),where I(R)is the set of all idempotents of R.In[11,12],the author generalized the result to skew power series ring R[[x;α]]and generalized power series ring [[RS,≤]].Cheng and Huang pointed out(see[9],Theorem 5)that the condition requiring all left semicentral idempotents being central is redundant in Theorem 3 of[10].It is shown that R[[x]]is right p.q.-Baer if and only if R is right p.q.-Baer and any countable subset of right semicentral idempotents has a generalized countable join.This properly generalized the result in[10],Theorem 3.Inspired by the results above,in this paper we investigate the principal quasi-Baerness of skew generalized power series rings.Let R be a ring,(S,≤) be a strictly totally ordered monoid such that 0≤s for all s∈S.It is shown that if λ is a weakly rigid homomorphism,then the skew generalized power series ring[[RS,≤,λ]]is right p.q.-Baer if and only if R is right p.q.-Baer and any S-indexed subset of Sr(R)has a generalized join in Sr(R).This generalize the results such as Theorem 5 in[11],Theorem 2.1 in[12],Theorem 5 in[9]and Theorem 4 in[13].

For a nonempty subset Y of R,rR(Y)denotes the right annihilator of Y in R.Let C(R) be the set of all central elements of R.

Let(S,≤)be an ordered set.Recall that(S,≤)is artinian if every strictly decreasing sequence of elements of S is finite,and that(S,≤)is narrow if every subset of pairwise order-incomparable elements of S is finite.Let S be a commutative monoid.Unless stated otherwise,the operation of S is denoted additively,and the neutral element is denoted by 0.The following Definition is due to[14,15].

Let(S,≤)be a strictly ordered monoid(that is,(S,≤)is an ordered monoid satisfying the condition that,if s,s′,t∈S and s＜s′,then s+t＜s′+t),and R a ring.Let[[RS,≤]] be the set of all maps f:S→R such that supp(f)={s∈S|f(s)/=0}is artinian and narrow.With pointwise addition,[[RS,≤]]is an abelian additive group.For every s∈S and f,g∈[[RS,≤]],let

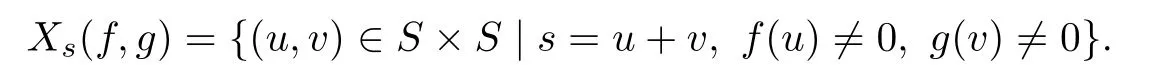
It follows from[16]that Xs(f,g)is finite.Denote by End(R)the set of all ring homomorphisms from R to R.Let λ:S→End(R)be a map satisfying the following condition:

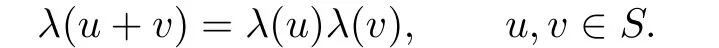
For any s∈S and f,g∈[[RS,≤]],define fg:S→R via

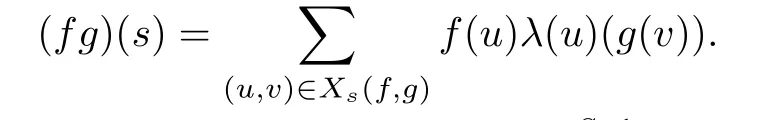
With the addition and the multiplication as above,([[RS,≤]],+,·)becomes a ring,which we denote by[[RS,≤,λ]],and call it the skew generalized power series ring related to λ.Theelements of[[RS,≤,λ]]are called generalized power series with coefficient in R and exponents in S.If λ(s)=1 for any s∈S,then[[RS,≤,λ]]=[[RS,≤]]is the ring of generalized power series.For more details and examples of generalized power series rings,see[17–21].

For example,let α be a ring endomorphism of R,and S=N∪{0}be endowed with the usual order.Def i ne λ:S→End(R)via λ(0)=1,and λ(k)=αkfor any k∈N.Then [[RS,≤,λ]]=R[[x;α]],the usual skew power series rings.Let α be a ring automorphism of R,and S=Z be endowed with the usual order.Define λ(k)=αkfor any k∈Z. Then[[RS,≤,λ]]=R[[x,x-1;α]],the usual skew Laurent series rings.Further example is Example 2.2 of[14].

Let r∈R.Define a mapping cr∈[[RS,≤,λ]]as follows:

For every 0/=f∈[[RS,≤,λ]],denote by π(f)the set of minimal elements of supp(f). Then π(f)is a nonempty finite set,consisting of pairwise order incomparable elements.If π(f)consists only of one element s,we write π(f)=s.

2 Main Results

Let α be a ring endomorphism of R.According to[6],α is called a rigid endomorphism if rα(r)=0 implies r=0 for r∈R.A ring R is called to be α-rigid if there exists a rigid endomorphism α of R.Generalizing these concepts,Liu[11]introduced the weakly rigid endomorphism(see[11],Definition 1).Let α be a ring endomorphism of R.Then α is called a weakly rigid endomorphism if α is a monomorphism,and if a,b∈R are such that ab=0 then aα(b)=α(a)b=0.Any rigid endomorphism is weakly rigid.But the converse is not true.Let α be a weakly rigid endomorphism of R.It is easy to check that if aα(b)=0 or α(a)b=0,then ab=0 for any a,b∈R.We say that λ:S→End(R)is a weakly rigid homomorphism if for any s∈S,λ(s)is a weakly rigid endomorphism of R.The following result appeared in[14].

Lemma 2.1[14]Let λ be a weakly rigid homomorphism.Then

(1)λ(0)=1;

(2)for any s∈S and e2=e∈R,λ(s)(e)=e.

Recall from[3]that an idempotent e∈R is left(resp.right)semicentral in R if ere=re (resp.ere=er)for all r∈R.Equivalently,e2=e∈R is left(resp.right)semicentral if eR (resp.Re)is an ideal of R.Since the right annihilator of a right ideal is an ideal,we see that the right annihilator of a principal right ideal is generated by a left semicentral idempotent in a right p.q.-Baer ring.The set of all left(resp.right)semicentral idempotents of R is denoted by Sℓ(R)(resp.Sr(R)).

Lemma 2.2[7]Let e∈R be an idempotent.Then the following conditions are equivalent:

(1)e∈Sℓ(R);

(2)1-e∈Sr(R);

(3)(1-e)Re=0;

(4)eR is an ideal of R;

(5)R(1-e)is an ideal of R.

Lemma 2.3[14]Let R be a ring,(S,≤)be a strictly totally ordered monoid satisfying that 0≤s for all s∈S,and λ:S→End(R)be a weakly rigid homomorphism.If φ∈[[RS,≤,λ]] is a left semicentral idempotent,then φ(0)∈Sℓ(R)and φ[[RS,≤,λ]]=cφ(0)[[RS,≤,λ]].

Let C⊆Sr(R).We say that C is S-indexed if there exists an artinian and narrow subset I of S such that C is indexed by I.

Definition 2.1Let G be an S-indexed subset of Sr(R).We say that G has a generalized join in Sr(R)if there exists e∈Sr(R)such that

(1)eie=eifor any ei∈G;

(2)for any a∈R and ei∈G,if eia=ei,then ea=e.

Let I(R)be the set of all idempotents of R,and G be an S-indexed subset of I(R).Liu[12]defined the generalized join of G in I(R),and showed that if R is a ring with Sℓ(R)⊆C(R), and(S,≤)is a strictly totally ordered monoid satisfying that 0≤s for all s∈S,then the generalized power series ring[[RS,≤]]is right p.q.-Baer if and only if R is right p.q.-Baer and any S-indexed subset of I(R)has a generalized join in I(R).From[9]we know that if G⊆Sr(R),then the generalized join defined in[10]is equivalent to the generalized join we defined as above.For the skew generalized power series ring,we have the following result, which is a generalization of Theorem 2.1 in[12].

Theorem 2.1Let R be a ring,(S,≤)be a strictly totally ordered monoid,and λ:S→End(R)be a weakly rigid homomorphism.If R is right p.q.-Baer and any S-indexed subset of Sr(R)has a generalized join in Sr(R),then[[RS,≤,λ]]is right p.q.-Baer.

Proof.Suppose that φ∈[[RS,≤,λ]].Then for any t∈supp(φ),there exists a left semicentral idempotent et∈R such that

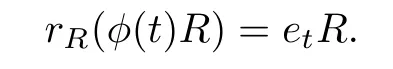
Since supp(φ)is artinian and narrow,by Lemma 2.2,{1-et|t∈supp(φ)}is an S-indexed subset of Sr(R).By the hypothesis,{1-et|t∈supp(φ)}has a generalized join f in Sr(R). Thus

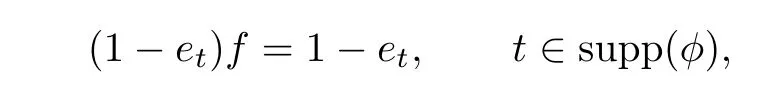
and so

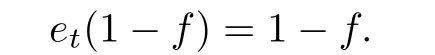
For any α∈[[RS,≤,λ]]and any s∈S,noting that λ is weakly rigid,by Lemma 2.1,we have

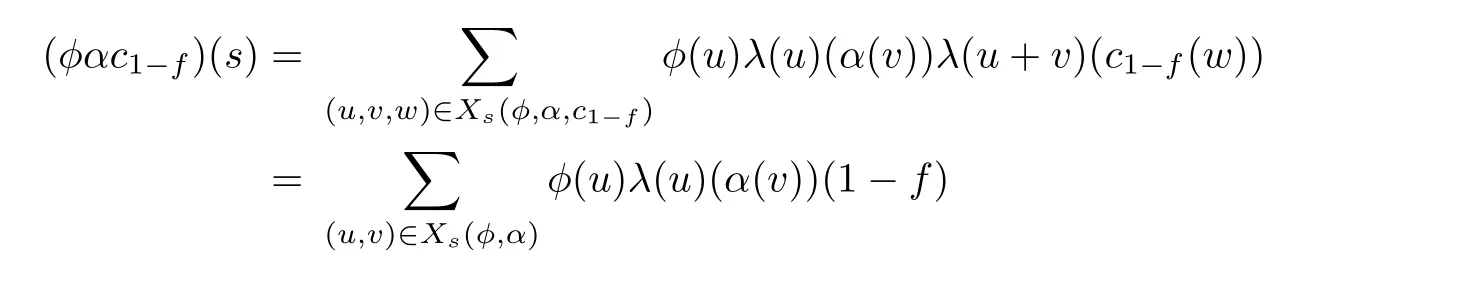
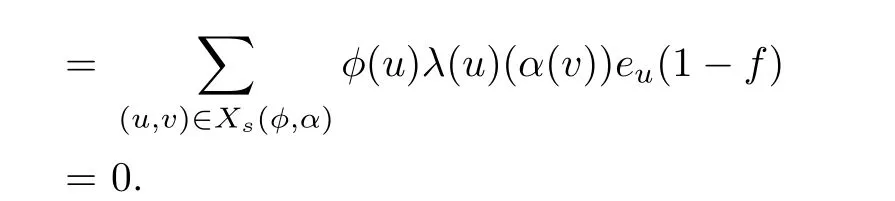
Thus

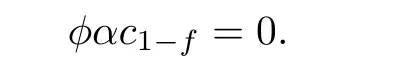
This means that

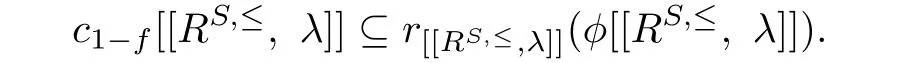
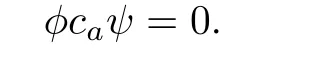
Denote

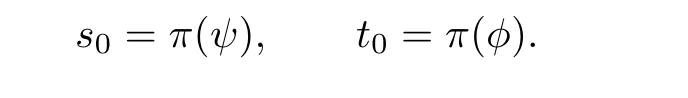
Clearly,

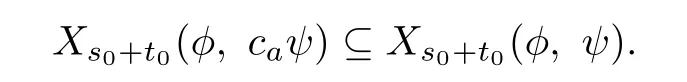
Denote

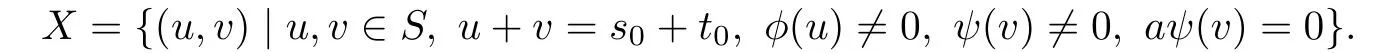
Then

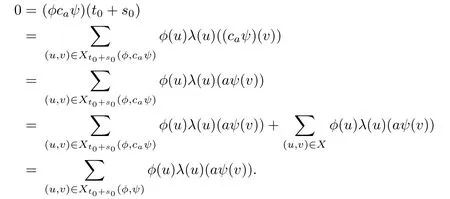
Clearly,

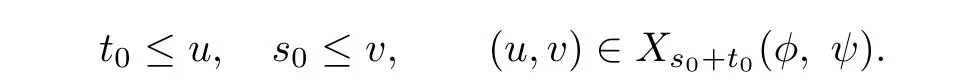
If t0＜u,noting that the order≤is strict,we have

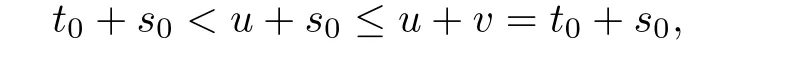
a contradiction.Hence

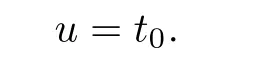
Similarly,

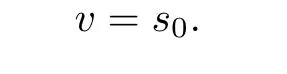
Thus

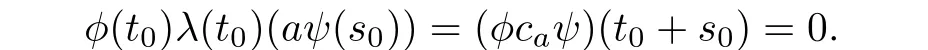
Since λ(t0)is weakly rigid,we have

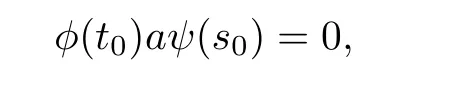
and so

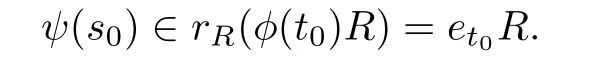
Hence

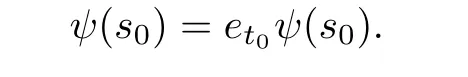
Now let w∈S with s0+t0≤w.Suppose that for any s∈supp(ψ)and any t∈supp(φ), if s+t＜w,then ψ(s)=etψ(s).We show that if s∈supp(ψ)and t∈supp(φ)are such that s+t=w,then

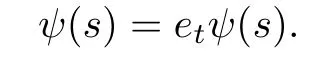
By analogy with the above proof,for any a∈R,we have

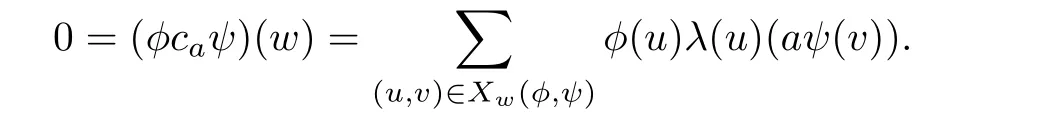
If there are not s∈supp(ψ)and t∈supp(φ)such that s+t=w,then the conclusion holds.Now suppose that s∈supp(ψ)and t∈supp(φ)are such that s+t=w.Then (t,s)∈Xw(φ,ψ).For convenience we write

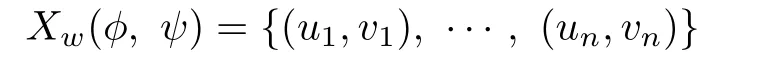
with

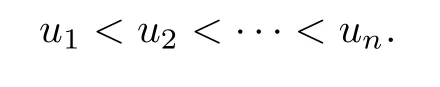
Then

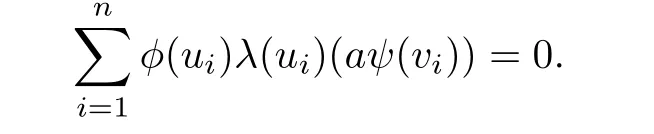
Since a is arbitrary,we may replace a byfor arbitrary a′∈R into the equation above. Note that λ is weakly rigid,by Lemma 2.1,we have

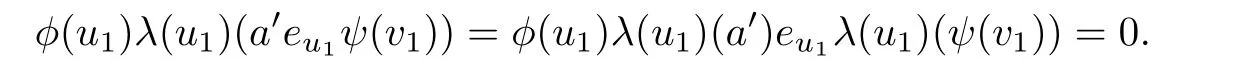
Thus

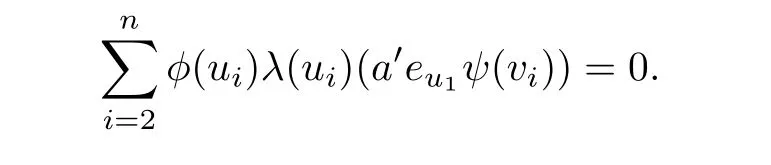
Note that

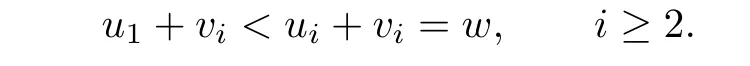
By hypothesis,we have

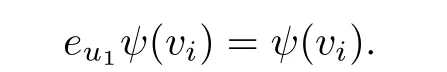
Hence

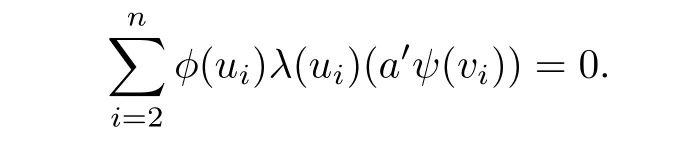
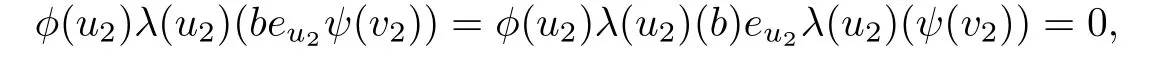
we have

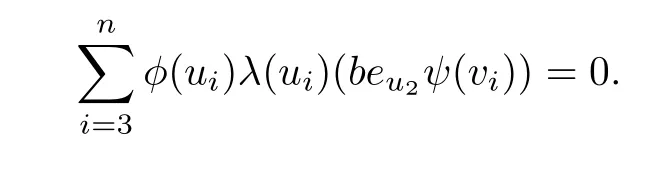
Notice that

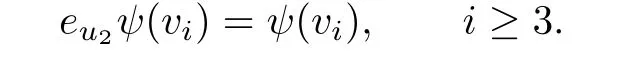
Then

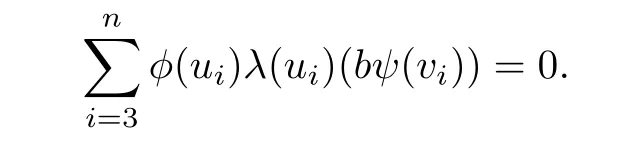
Continuing in this manner,we have

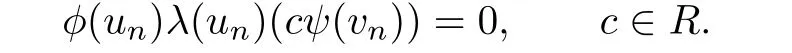
Thus

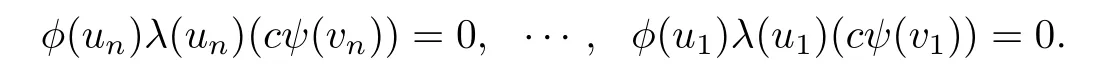
Since λ is weakly rigid,we have

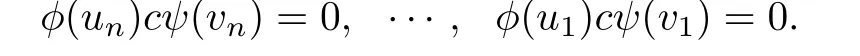
Thus

Then

Therefore,by transfinite induction,we have shown that for any s∈supp(ψ)and any t∈supp(φ),

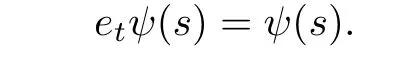
Thus

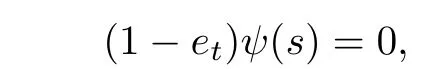
and then

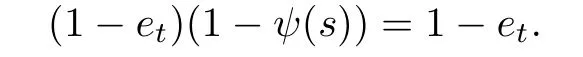
Since f is the generalized join of{1-et|t∈supp(φ)},we have

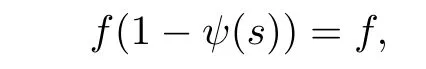
and so

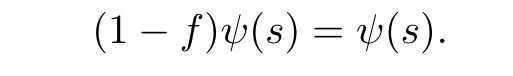
Clearly,

Thus

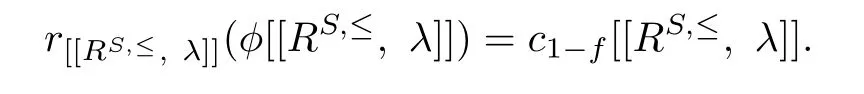
Hence[[RS,≤,λ]]is right p.q.-Baer.The proof is completed.

Theorem 2.2Let R be a ring,(S,≤)be a strictly totally ordered monoid satisfying that 0≤s for all s∈S,and λ:S→End(R)be a weakly rigid homomorphism.If[[RS,≤,λ]]is right p.q.-Baer,then R is right p.q.-Baer and any S-indexed subset of Sr(R)has a generalized join in Sr(R).

Proof.Let a∈R.Since[[RS,≤,λ]]is right p.q.-Baer,there exists a left semicentral idempotent h∈[[RS,≤,λ]]such that

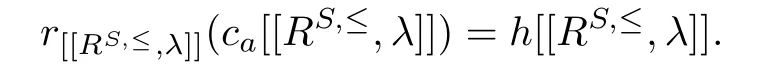
By Lemma 2.3,h(0)∈Sℓ(R)and

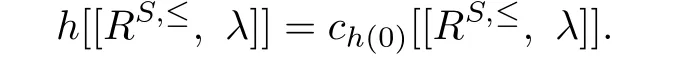
Thus for any r∈R,

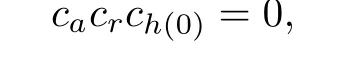
which implies that

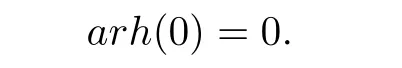
Hence h(0)∈rR(aR).Conversely,suppose that b∈rR(aR).Note that λ is weakly rigid. So for any ψ∈[[RS,≤,λ]]and any x∈S,we have

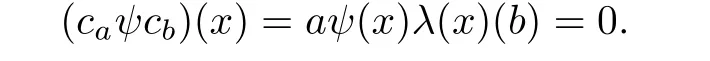
This implies that

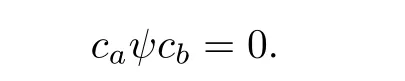
Hence

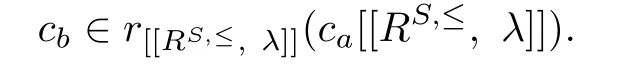
Then

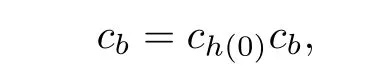
and so

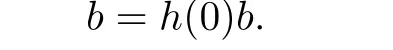
This implies that

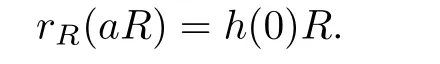
Hence R is right p.q.-Baer.

Suppose that G is an S-indexed subset of Sr(R).Then there exists an artinian and narrow subset I of S such thatDefine φ∈[[RS,≤,λ]]via

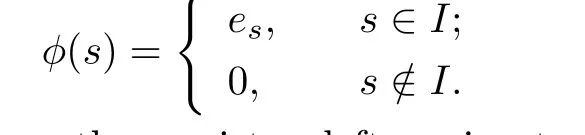
Since[[RS,≤,λ]]is right p.q.-Baer,there exists a left semicentral idempotent h∈[[RS,≤,λ]] such that

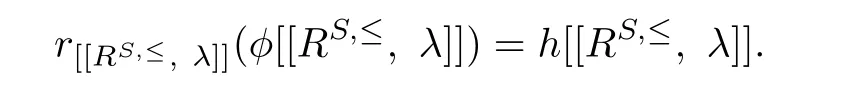
By Lemma 2.3,h(0)∈Sℓ(R)and

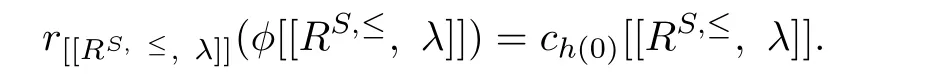
Let

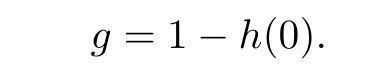
By Lemma 2.2,g∈Sr(R).We show that g is the generalized join of G in Sr(R). Since

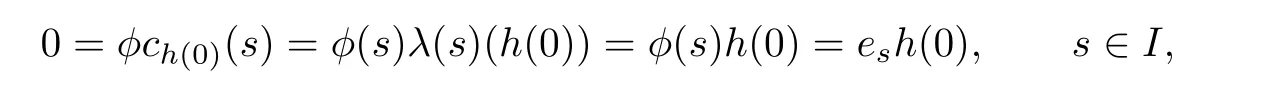
we have

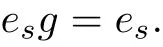
Now let a∈R be such that

Then

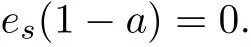
Since es∈Sr(R),it follows that

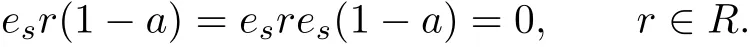
Since λ is weakly rigid,we have

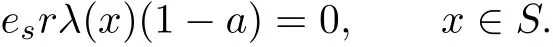
Then for any ψ∈[[RS,≤,λ]]and any s∈S,we have

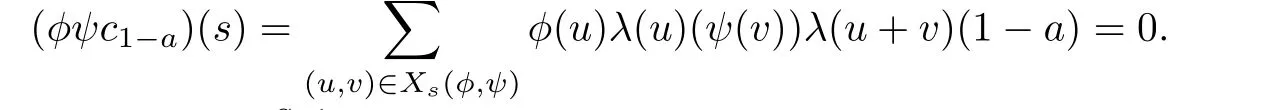
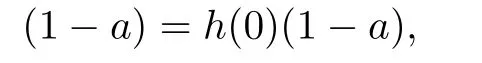
and then

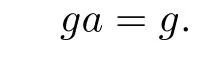
Hence g is the generalized join of G in Sr(R).The proof is completed.

Corollary 2.1Let R be a ring,(S,≤)be a strictly totally ordered monoid satisfying that 0≤s for all s∈S,and λ:S→End(R)be a weakly rigid homomorphism.Then the following conditions are equivalent:

(1)[[RS,≤,λ]]is right p.q.-Baer;

(2)R is right p.q.-Baer and any S-indexed subset of Sr(R)has a generalized join in Sr(R).

Corollary 2.2Let R be a ring,(S1,≤1),···,(Sn,≤n)be strictly totally ordered monoids, and λ:S1×···×Sn→End(R)be a weakly rigid homomorphism.Denote by(lex≤)and (revlex≤)the lexicographic order and the reverse lexicographic order,respectively,on the monoid S1×···×Sn.

(1)If R is right p.q.-Baer and any(S1×···×Sn,(lex≤))-indexed subset of Sr(R)has a generalized join in Sr(R),thenis right p.q.-Baer.

(2)If(Si,≤i),i=1,2,···,n,also satisfy the condition that 0≤is for all s∈Si, thenis right p.q.-Baer if and only if R is right p.q.-Baer and any (S1×···×Sn,(lex≤))-indexed subset of Sr(R)has a generalized join in Sr(R).

Proof.It is easy to verify that(S1×···×Sn,(lex≤))is a strictly totally ordered monoid, and(0,···,0)(lex≤)(s1,···,sn)for any(s1,···,sn)∈S1×···×Sn.Thus the results follow from Theorems 2.1 and 2.2.

Corollary 2.3Let α be a weakly rigid endomorphism of R.Then the following conditions are equivalent:

(1)R[[x;α]]is right p.q.-Baer;

(2)R is right p.q.-Baer and any countable subset of Sr(R)has a generalized join in Sr(R).

[1]Kaplansky I.Rings of Operators.New York:Benjamin,1968.

[2]Clark W E.Twisted matrix units semigroup algebras.Duke Math.J.,1967,34:417–424.

[3]Birkenmeier G F,Kim J Y,Park J K.Polynomial extensions of Baer and quasi-Baer rings.J. Pure Appl.Algebra,2001,159:25–42.

[4]Birkenmeier G F,Kim J Y,Park J K.On quasi-Baer rings.Contemp.Math.,2000,259:67–92.

[5]Birkenmeier G F,Kim J Y,Park J K.Quasi-Baer ring extensions and biregular rings.Bull. Austral.Math.Soc.,2000,61:39–52.

[6]Hong C Y,Kim N K,Kwak T K.Ore extensions of Baer and p.p.-rings.J.Pure Appl.Algebra, 2000,151(3):215–226.

[7]Birkenmeier G F,Kim J Y,Park J K.Principally quasi-Baer rings.Comm.Algebra,2001,29: 639–660.

[8]Birkenmeier G F,Kim J Y,Park J K.On polynomial extensions of principally quasi-baer rings.Kyungpook Math.J.,2000,40:247–254.

[9]Cheng Y W,Huang F K.A note on extensions of principal quasi-Baer rings.Taiwanese.J. Math,2008,12:1721–1731.

[10]Liu Z K.A note on principal quasi-Baer rings.Comm.Algebra,2002,30:3885–3890.

[11]Liu Z K.Principal quasi-Baerness of skew power series rings.J.Math.Res.Exposition,2005, 25:197–203.

[12]Liu Z K.Principal quasi-Baerness of rings of generalized power series.Northeast.Math.J., 2007,23:283–292.

[13]Liu Z K.Principal quasi-Baerness of Laurent series rings.Acta Math.Sin.,Chinese Ser.,2002, 45:1107–1112.

[14]Liu Z K.Triangular matrix representations of rings of generalized power series.Acta Math. Sinica,Engl.Ser.,2006,22:989–998.

[15]Mazurek R,Ziembowski M.On von Neumann regular rings of skew generalized power series. Comm.Algebra,2008,36:1855–1868.

[16]Ribenboim P.Semisimple rings and von Neumann regular rings of generalized power series.J. Algebra,1997,198:327–338.

[17]Liu Z K.Morita duality for the rings of generalized power series.Acta Math.Sinica,Engl. Ser.,2002,18:245–252.

[18]Liu Z K.Special properties of rings of generalized power series.Comm.Algebra,2004,32: 3215–3226.

[19]Ribenboim P.Noetherian rings of generalized power series.J.Pure Appl.Algebra,1992,79: 293–312.

[20]Varadarajan K.Generalized power series modules.Comm.Algebra,2001,29:1281–1294.

[21]Varadarajan K.Noetherian generalized power series rings and modules.Comm.Algebra,2001, 29:245–251.

16W60,16S50

A

1674-5647(2013)04-0335-10

Received date:Jan.10,2011.

The Youth Foundation(QN2012-14)of Hexi University.

E-mail address:zhangwru@163.com(Zhang W R).