Invariants for Automorphisms of the Underlying Algebras Relative to Lie Algebras of Cartan Type

SUN XIU-MEI,WANG JING-GUO AND LIU WEN-DE

(School of Mathematical Sciences,Harbin Normal University,Harbin,150025)

Communicated by Du Xian-kun

Invariants for Automorphisms of the Underlying Algebras Relative to Lie Algebras of Cartan Type

SUN XIU-MEI,WANG JING-GUO AND LIU WEN-DE*

(School of Mathematical Sciences,Harbin Normal University,Harbin,150025)

Communicated by Du Xian-kun

Let X denote a finite or in finite dimensional Lie algebra of Cartan type W,S,H or K over a field of characteristic p≥3.In this paper it is proved that certain filtrations of the underlying algebras are invariant under the admissible groups relative to Lie algebras of Cartan type X.

Lie algebra, filtration,automorphism

1Introduction

Premet and Strade[1]finished the complete classification of finite dimensional simple Lie algebras over an algebraically closed field of characteristic p＞3.We know that Lie algebras of Cartan type play an important role in the modular Lie algebra theory.In[2–6],the automorphism groups of Lie algebras of Cartan type were sufficiently studied.In this paper we obtain the invariance of certain filtration structures of the underlying algebras of finite or infinite dimensional Lie algebras of Cartan type.The results are used to establish a correspondence between the admissible automorphism groups of the underlying algebrasrelative to X and the automorphism group of X,and an isomorphism from the admissible homogeneous automorphism group ofonto the homogeneous automorphism group of X, where X stands for a finite or an inf i nite dimensional Lie algebra of Cartantype W,S,H or K.

2Beginning

In this paper F denotes a field of characteristic p≥3.Z+and N denote the positive integer set and nonnegative integer set,respectively.Fix an integer m＞2 and the index set I:={1,2,···,m}.Denote by Nmthe additive monoid of m-tuples of nonnegative integers. Suppose m=2r or 2r+1,where r∈Z+.Set

We recall the necessary definitions and facts.Denote bythe divided power algebra with F-basis{xα|α∈Nm}.For i∈I,let∂ibe the special derivation ofsuch that∂i(xα)=xα-εifor all α=(α1,···,αm)∈Nm(see[4,7]).Hereafter,εiis the m-tuple with 1 at the i-position and 0 elsewhere.For simplicity,write xifor xεi.Notice that

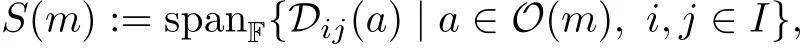
where Dij(a):=∂j(a)∂i-∂i(a)∂j;

where m=2r is even,

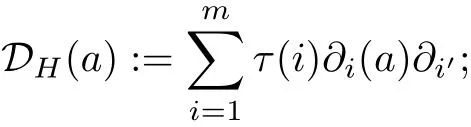
and

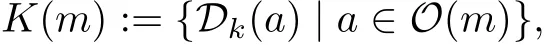
where m=2r+1 is odd and

Then X(m)is an inf i nite-dimensional subalgebra of W(m),where X=W,S,H or K.Letbe an m-tuple of positive integers.Then

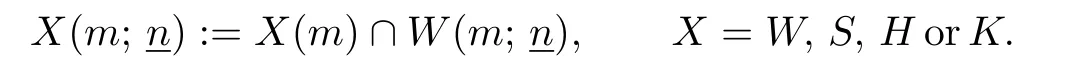
Then,the second derived subalgebrais a simple Lie algebra(see[4,6–7]).In the sequel,.For the sake of simplicity, in the following we often use X to stand for the Lie algebras X(m)oris identified with a subalgebra of ,where X=W,S,H or K.The underlying associative algebra of X is denoted by,or,in brief.Note that the underlying algebra ofis.

3Lemmas

In this section we establish several lemmas which is used in next section to prove the main result(Theorem 4.1).Recall the grading and filtration structures of Lie algebras of Cartan type and their underlying algebras.Given an m-tuple,similarly to[8–9],for i∈I we put

Hereafter,for α=(α1,···,αm)and γ=(γ1,···,γm),we write αγ:=(α1γ1,···,αmγm) andare Z-graded.We note thatand,for i∈I.Of course,and W have the associated f i ltration structures,denoted byand,respectively.By setting,X is f Thenand⊕i ltered bywhere X=W,S,H or K.This paper is mainly involved in γ=1orwhose grading is denoted by.Note that X is a Z-graded subalgebra ofcan be viewed as a free graded module over⊕.We also note that in a natural way. For simplicity,where X=W,S or H,are denoted byX[i]and Xi,respectively.

Now we assemble certain known results in the following lemma,on which the present paper is based.

Lemma 3.1[2-3,5,10]The following statements hold:

(ii)ΦX:Autis an isomorphism of groups.

Moreover,Wilson[5]determined the factors AutiX/Auti+1X of the normal series of AutX.Further detailed background information on the automorphisms ofor X(m) can be found in[2–3,5–6,11].

Lemma 3.2Suppose that{E1,···,Es}⊂W is.Then{Pr[-1]E1,···, Pr[-1]Es}is alsowhere Pr[-1]is the projection of W onto W[-1].In particular,{Pr[-1]E1,···,Pr[-1]Es}is F-independent.

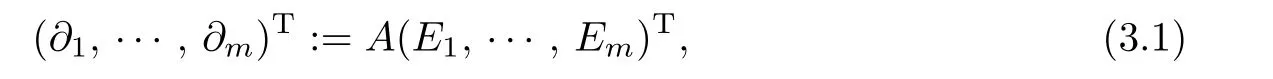
where Pr0is the projection of W onto W0.It follows from(3.1)that

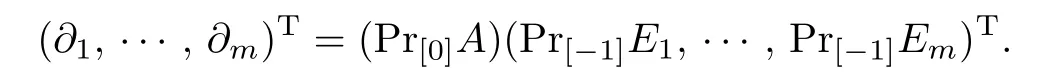
As{∂1,···,∂m}is an F-basis of W[-1],we obtain from the equation above that{Pr[-1]E1, ···,Pr[-1]Em}is also an F-basis of W[-1].Note that{∂1,···,∂m}is anof W.We see that

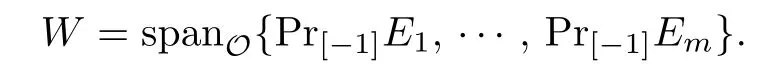
In the sequel,we adopt the convention that,ifis under consideration,implies that k＜pniin the case,and that k∈Z is arbitrary in the case.

Lemma 3.3Let X=W,S or H.Suppose thatwhere j∈I,and k=1 or p|k. Then there exists tj∈I such that xkεj∂tj∈X.it is clear that k+1≤pnj-1.Note that

Proof.In the case

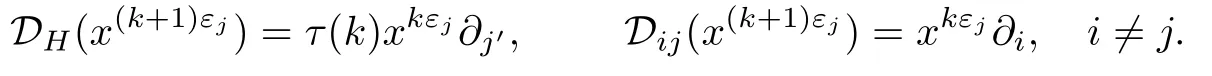
The desired result follows.

Lemma 3.4and γ∈Zm+.

Proof.Note that each basis elementand eachcan be generated by xiand xkεi,where k≡0(mod p).So(i)follows.By setting j=0 in(i),we obtain(ii).(iii)is straightforward.

4Main Result

The following theorem asserts that the filtrationpossesses certain invariances, where X=W,S,H or K.

Theorem 4.1The filtrationis invariant under Aut(:X),where X= W,S,H or K is of f i nite or inf i nite dimension.

Case(i):X=W,S or H.Note thatAutX.By Lemma 3.3,for xkεj∈where k=1 or p|k,there exists a kj∈I such that∈X.By Lemma 3.1(i),we obtain that

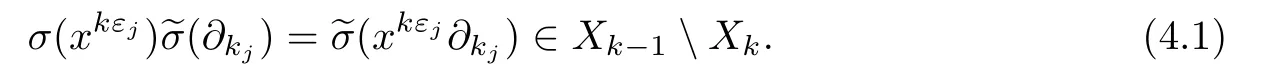
Since X[-1]=W[-1],one has,in addition,

It follows from(4.1)–(4.2)that.Now Lemma 3.4(ii)ensures thatis invariant under σ.

Case(ii):X=K.Note that

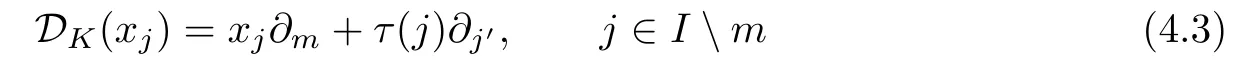
and

We have

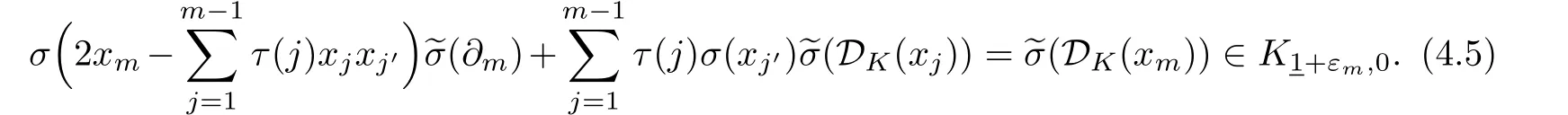
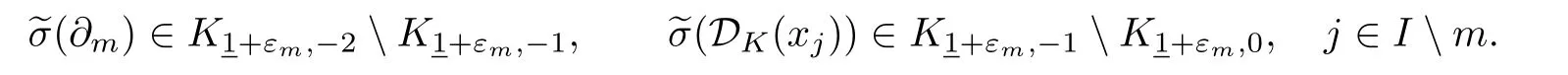
Consequently,

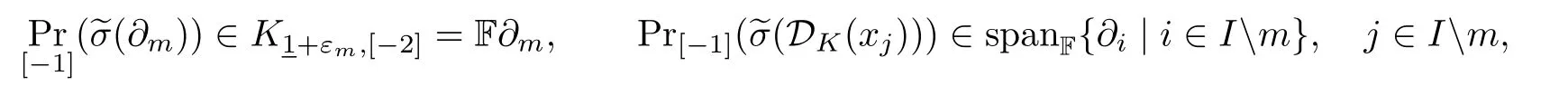
and Pr[-1]is the projection of W onto W[-1].Notice that

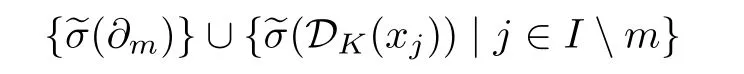
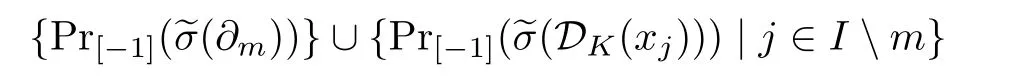
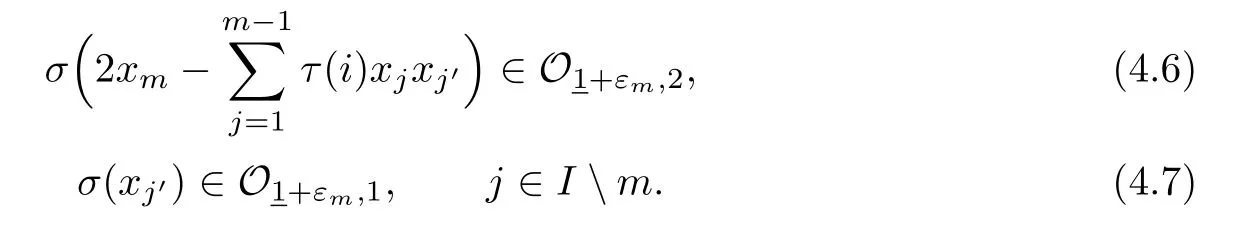
It follows from(4.6)–(4.7)that

Suppose that k≡0(mod p)and j∈Im.Then we have

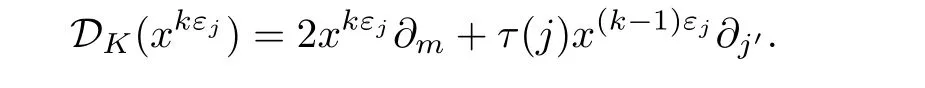
Using(4.3)and k≡0(mod p),we have

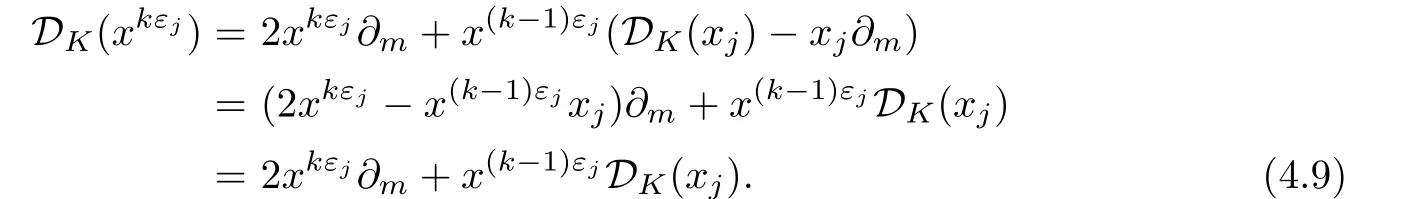
By Lemma 3.1(i),it follows that

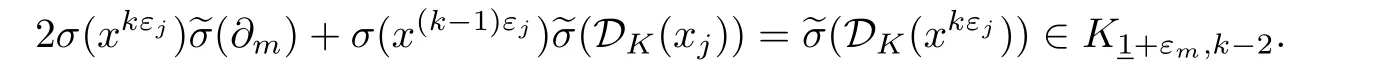
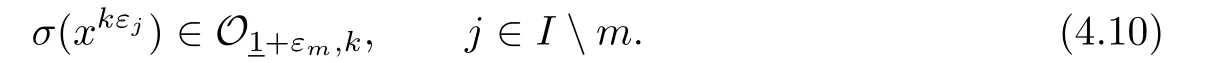
Consequently,

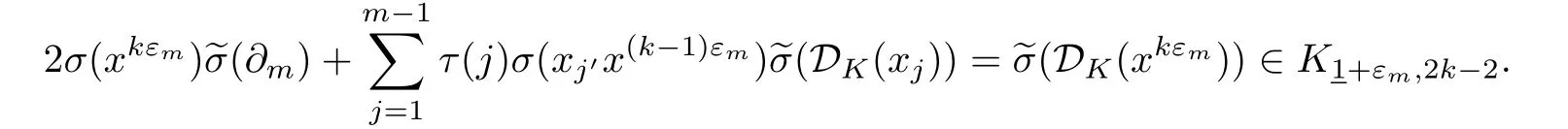
This yields as in the above,

Using Lemma 3.4(ii),one gets the desired result from(4.7),(4.8),(4.10)and(4.12).

i cation.J.Algebra,2008,320:3559–3604.

[2]Jin N.Ad-nilpotent elements,quasi-nilpotent elements and invariant filtrations of inf i nitedimensional Lie algebras of Cartan type.Sci.China Ser.A,1992,35:1191–1200.

[3]Kac V G.Description of filtered Lie algebras with graded Lie algebras of Cartan type are associated.Math.USSR Izv.,1974,8:801–835.

[4]Strade H.Simple Lie algebras over Fields of Positive Characteristic,I.Structure theory.Berlin-New York:Walter de Gruyter,2004.

[5]Wilson R L.Automorphisms of graded Lie algebras of Cartan type.Comm.Algebra,1975,3: 591–613.

[6]Wilson R L.A structural characterization of the simple Lie algebras of generalized Cartan type over fields of prime characteristic.J.Algebra,1976,40:418–465.

[7]Strade H,Farnsteiner R.Modular Lie Algebras and Their Representations.Monographys and Textbooks in Pure and Applied Math.vol 116.New York:Marcel Dekker Inc.,1988.

[8]Kac V G.On the classification of the simple Lie algebras over a field with nonzero characteristic. Math.USSR Izv.,1970,4:391–413.

[9]Shu B,Shen G Y.Automorphisms and forms of Lie algebras of Cartan type.Comm.Algebra, 1995,23:5243–5268.

[10]Wilson R L.Classification of generalized Witt algebras over algebraically closed fields.Trans. Amer.Math.Soc.,1971,153:191–210.

[11]Kostrikin A I,Shafarevic I R.Graded Lie algebras of finite characteristic.Math.USSR Izv., 1969,3:237–304.

[1]Premet A,Strade H.Simple Lie algebras of small characteristic VI.Completion of the classif

17B50,17B40

A

1674-5647(2013)04-0329-06

Received date:Sept.20,2010.

The NSF(11171055)of China,the NSF(JC201004 and A200903)of Heilongjiang Province of China and the NSF(12511349)of Heilongjiang Educational Committee of China.

*Corresponding author.

E-mail address:sxm@hrbnu.edu.cn(Sun X M),wendeliu@ustc.edu.cn(Liu W D).