An Extension of Chebyshev's Maximum Principle to Several Variables

MENG ZHAO-LIANGAND LUO ZHONG-XUAN,2

(1.School of Mathematical Sciences,Dalian University of Technology,Dalian, Liaoning,116024) (2.School of Software,Dalian University of Technology,Dalian,Liaoning,116024) Communicated by Ma Fu-ming

An Extension of Chebyshev's Maximum Principle to Several Variables

MENG ZHAO-LIANG1AND LUO ZHONG-XUAN1,2

(1.School of Mathematical Sciences,Dalian University of Technology,Dalian, Liaoning,116024) (2.School of Software,Dalian University of Technology,Dalian,Liaoning,116024) Communicated by Ma Fu-ming

In this article,we generalize Chebyshev's maximum principle to several variables.Some analogous maximum formulae for the special integration functional are given.A sufficient condition of the existence of Chebyshev's maximum principle is also obtained.

cubature formula,orthogonal polynomial,Chebyshev's maximum principle,nonstandard Gaussian quadrature

1 Introduction

Let ω be a nonnegative weight function on(-∞,∞)for which

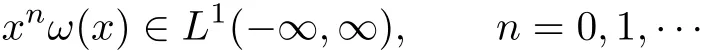
We construct a sequence of orthonormal polynomials

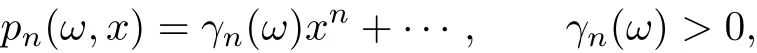
to satisfy

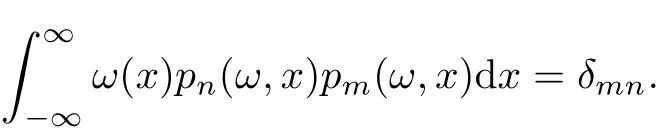
It is well known that all zeros xknof pn(ω)are real and simple.Let us denote by Xn(ω) the greatest zero of pn(ω).The sequence{Xn(ω)}is increasing and,by virtue of a result of

Chebyshev(see[1–4]),

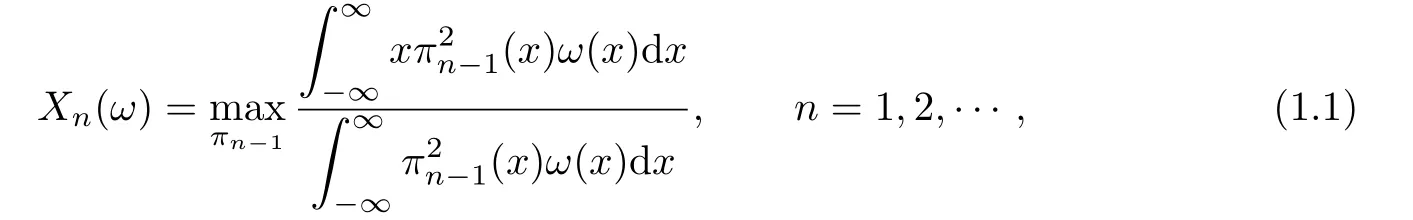
the maximum being attained forHere and in what follows πkdenotes an arbitrary real polynomial/=0 of degree≤k.For even weight,(1.1)can be extended to

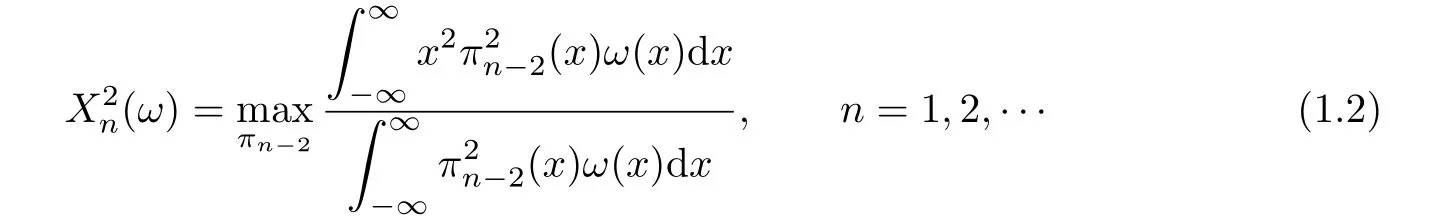
The essence of relations(1.1)and(1.2)lies in the fact that Gauss quadrature formula always exists in the case of one dimension and all the weights are positive.

Let us turn to the case of higher dimension.Let Πdbe the space of all polynomials in d variables,andthe subspace of polynomials of total degree≤n.Let L be a positive definite linear functional acting on Πd.According to[5],a cubature formula of degree 2n-1 withnodes is called a Gaussian cubature formula and ifhascommon zeros,then L is called Gaussian,whereis a sequence of orthonormal polynomials with respect to L.If L is Gaussian,then the following result holds.

Theorem 1.1[6]Let l(x1,···,xd)be an arbitrary linear function with respect to. Then

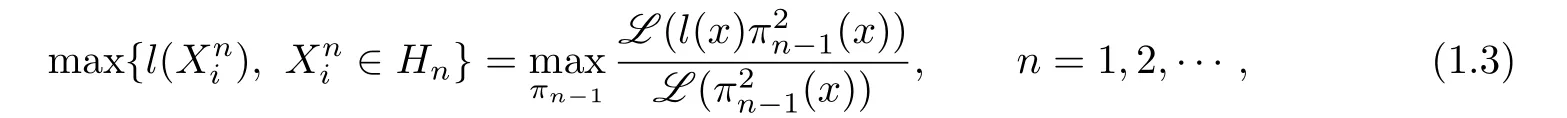
However,the Gaussian cubature formulae in several variables rarely exist although they indeed exist in some special cases.And it was shown that there does not have Gaussian cubature formulae for the standard regions.For the example of Gaussian cubature formulae, we can refer to Dunkl and Xu[5].

In this article,we present another generalization of Chebyshev's maximum principle which does not need L to be Gaussian.Our results can be applied to the classical integration of several variables,such as the integration over the sphere,the triangle,the square and so on.

This article is organized as follows.In Section 2,we present some maximum formulae for the integration over the disk and a further extension is given in Section 3.

2 Chebyshev's Maximum Principle over the Unit Disk

It is well known that there does not have Gaussian cubature formula with respect to the integration over the disk,but Bojanov and Petrova[7–8]presented a nonstandard Gaussian quadrature.They studied quadrature formulae for the unit disk D:={(x,y)|x2+y2≤1}, which are based on integrals over n chords.Their main result can be written as

Theorem 2.1[7]The quadrature formula

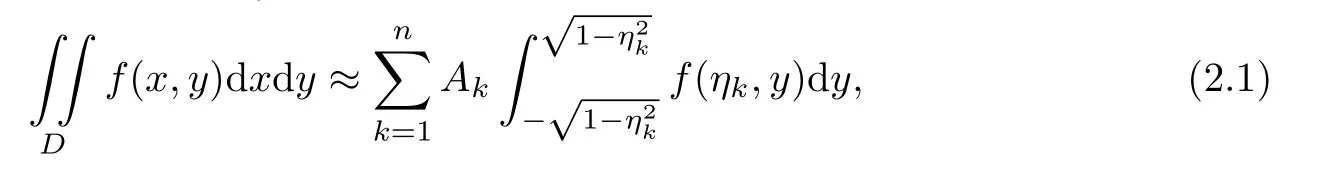
with

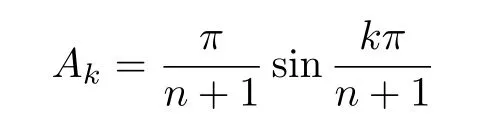
is exact for each polynomial,where η1,···,ηnare the zeros of Un(x)(the Chebyshev polynomial of second kind of degree n),that is,

Bojanov and Petrova[8]proved that the formula(2.1)is the only one(up to rotation) with this extremal property.Using Theorem 2.1 and the same notations,we can prove

Theorem 2.2

Proof.Since the cubature formula(2.1)is exact for all polynomial of degree at most 2n-1,

that is,

On the other hand,let

be the Lagrange interpolation polynomials based on the zeros of Un(x)which satisfy

Choosing k to be the index which satisfies(in this case k=1),we easily see that

Combining(2.3)and(2.4),we can obtain the result immediately.This completes the proof. Taking the symmetry into account,we can get the following corollary.

Corollary 2.1

By a simple rotation transformation,we have

Corollary 2.2

where l(x,y)=xcosθ+y sinθ,θ∈[0,2π).

Using Theorem 2.2 and Corollary 2.2,we have

Theorem 2.3Let l(x,y)=ax+by+c be a linear polynomial.Then

The proof can be easily given as Theorem 2.2.For the multivariate case,the corresponding result can be easily obtained by virtue of a similar result as Theorem 2.1(see[8]).

3 An Extension of Other Integral Functionals

Let L denote the same meaning as in Section 1 and

denote a group of linear functions with a2+b2/=0.If there exists a cubature formula

of degree 2n-1 and all Xk,k=1,···,N are the zeros of

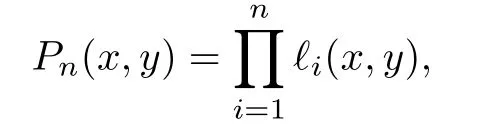
then for every l(x,y)=ax+by+c we have

Theorem 3.1

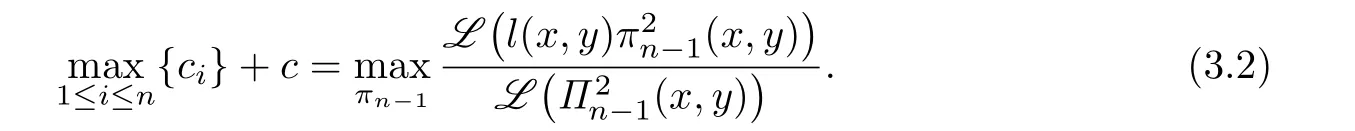
Proof.We note that{l(Xk)|1≤k≤N}={ck+c|1≤k≤N}.Then

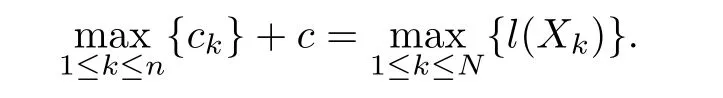
Let

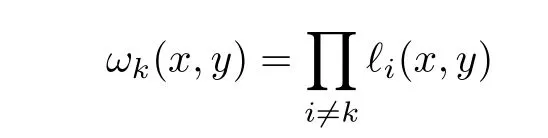
and choose k to be the index which satisfies

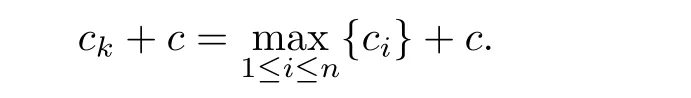
Then it is easy to check that

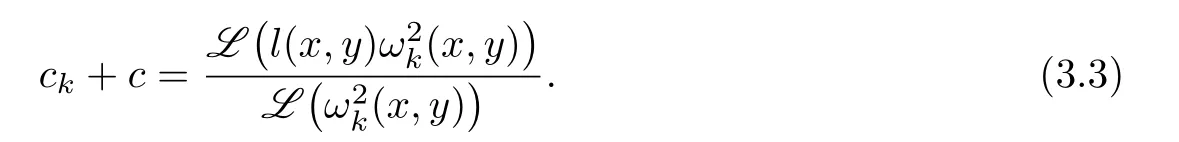
Thus we can take the same measure as Theorem 2.2 to prove it and the remaining is omitted.

We claim that Theorem 2.2 is a special case of Theorem 3.1.In fact,if we construct n Gauss quadrature formulas in(2.1)for every integration over the chord,then a formula of type(3.1)is obtained.Using Theorem 3.1,we can easily get

Corollary 3.1

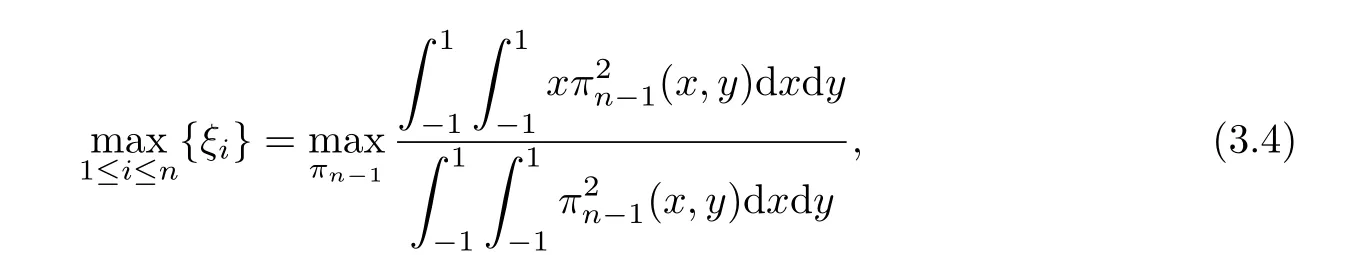
where ξi,i=1,···,n are the zeros of Legendre polynomial of degree n.

Corollary 3.2

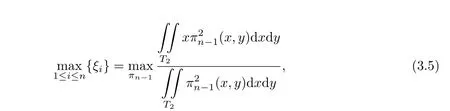
where T2={(x,y)|x≥0,y≥0,x+y≤1}and ξi,i=1,···,n are the zeros of a polynomial of degree n,orthogonal with respect to 1-x on[0,1].

Proof.

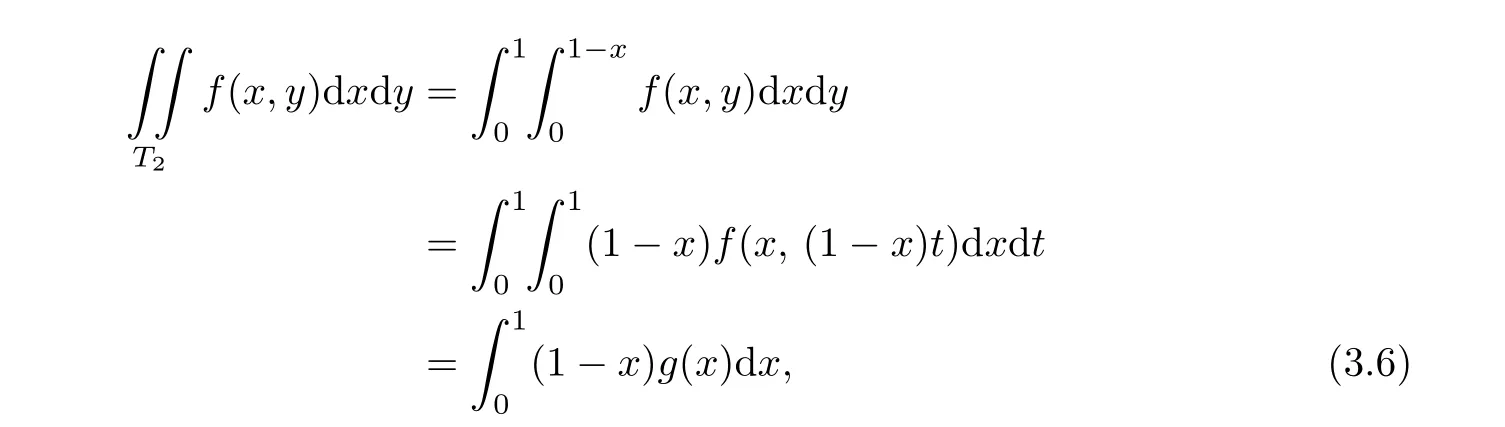
where

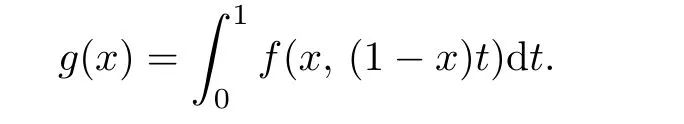
Let f(x,y)be a polynomial of degree at most 2n-1.Then it is easy to verify that g(x)is a one-dimensional polynomial of degree at most 2n-1.Hence,by using Gauss quadrature formula,we have

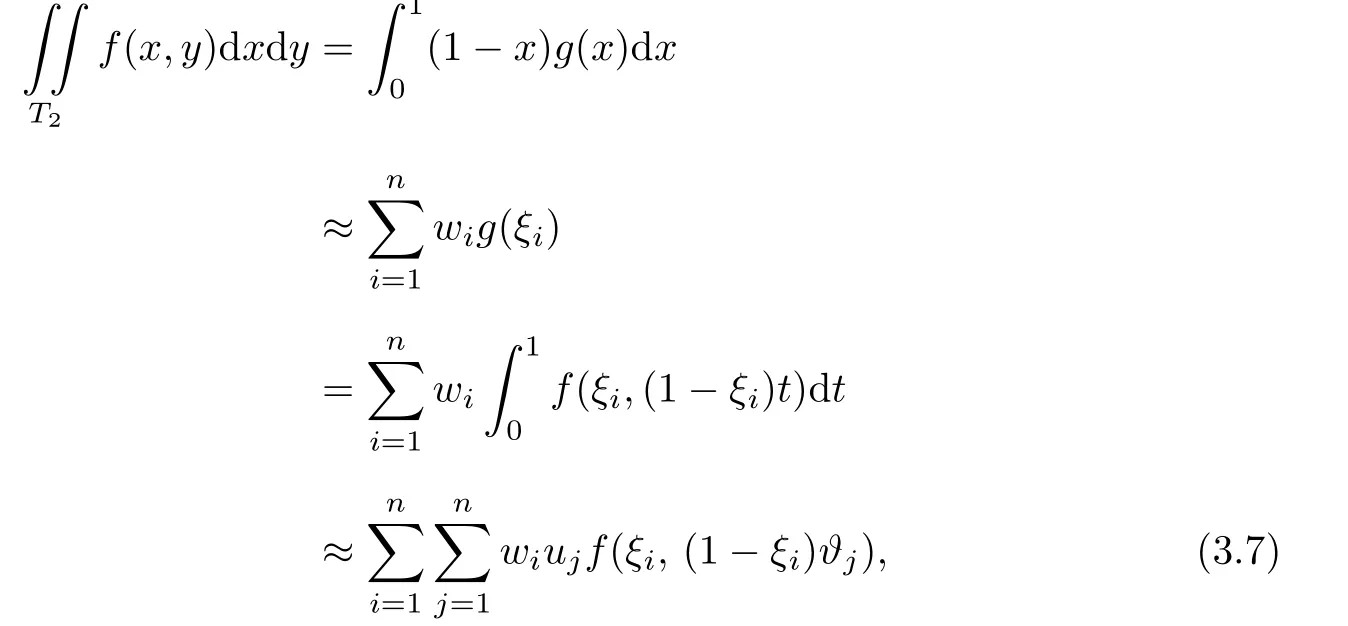
where wi,uj,1≤i,j≤n are positive numbers and it is exact if f is a polynomial of degree at most 2n-1.Then the proof follows from Theorem 3.1.

If we take

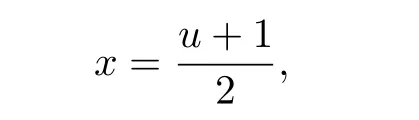
then

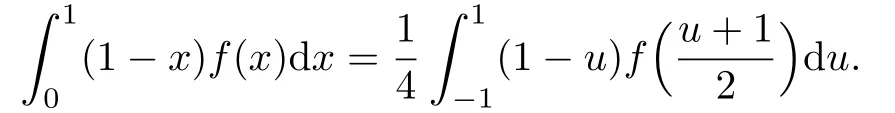
Hence,if Jn(x)denotes the Jacobian polynomial of degree n,orthogonal with respect to 1-x on[-1,1],then Jn(2x-1)is an orthogonal polynomial of degree n with respect to 1-x on[0,1].Thus,we can rewrite the above corollary as

Corollary 3.3

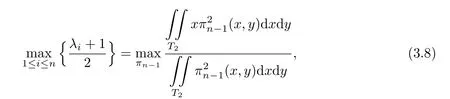
where λi,i=1,···,n are the zeros of the Jacobian polynomial Jn(x),orthogonal with respect to 1-x on[-1,1].

Remark 3.1If there exists a cubature formula of type(3.1),then Pn(x,y)must be an orthogonal polynomial of degree n.On the contrary,if we have an orthogonal polynomial ωn(x,y)which can be factorized as Pn(x,y),does there exist a cubature formula based on the zeros of ωn(x,y)and all the weights are positive?The number of the nodes is not important and even we do not need to know if it is an interpolation cubature formula.In fact,we only need to prove that there exists a cubature formula in which all the weights corresponding to every line are positive or negative simultaneously,but it is not simple.

Furthermore,the extension to higher dimension can be done completely similarly and we can get the same results.

[1]Freud G.On the greatest zero of an orthogonal polynomial I.Acta Sci.Math.(Szeged),1973, 34:91–97.

[2]Freud G.On the greatest zero of an orthogonal polynomial II.Acta Sci.Math.(Szeged),1974, 36:49–54.

[3]Freud G.On estimations of the greatest zeros of an orthogonal polynomial.Acta Math.Hungar., 1974,25:99–107.

[4]Freud G.On the greatest zero of an orthogonal polynomial.J.Approx.Theory,1986,46:16–24.

[5]Dunkl C F,Xu Y.Orthogonal Polynomials of Several Variables.Cambridge:Cambridge Univ. Press,2001.

[6]Wang R H,Zhou H.Chebyshev's maximum principle in several variables.J.Approx.Theory, 2003,123:276–279.

[7]Bojanov B,Petrova G.Numerical integration over a disc:A new Gaussian quadrature formula. Numer.Math.,1998,80:39–59.

[8]Bojanov B,Petrova G.Uniqueness of the Gaussian quadrature for a ball.J.Approx.Theory, 2000,104:21–44.

65D32

A

1674-5647(2013)04-0363-07

Received date:Dec.2,2011.

s:The NSF(10826071,61033012,19201004,11271060,61272371)of China and the Fundamental Research Funds for the Central Universities.

E-mail address:mzhl@dlut.edu.cn(Meng Z L).