A Gorni-Zampieri Pair of a Homogeneous Polynomial Map

LIU DA-YAN

(1.School of Mathematics,Jilin University,Changchun,130012) (2.School of Mathematics,Shandong University,Jinan,250100)

Communicated by Du Xian-kun

A Gorni-Zampieri Pair of a Homogeneous Polynomial Map

LIU DA-YAN1,2

(1.School of Mathematics,Jilin University,Changchun,130012) (2.School of Mathematics,Shandong University,Jinan,250100)

Communicated by Du Xian-kun

In this paper,we improve the algorithm and rewrite the function make-Pairing for computing a Gorni-Zampieri pair of a homogeneous polynomial map.As an application,some counterexamples to PLDP(dependence problem for power linear maps)are obtained,including one in the lowest dimension(n=48)in all such counterexamples one has found up to now.

Gorni-Zampieri pair,homogeneous dependence problem,power linear map

1 Introduction

Let F=(F1,···,Fn):Cn→Cnbe a polynomial map and JF the Jacobian matrix of F. The famous Jacobian Conjecture asserts that F is invertible if detJF∈C*;see Introduction of[1]or[2].A polynomial map of the form F=X+H is called homogeneous of degree d if each Hiis homogeneous of degree d.And a polynomial map of the form

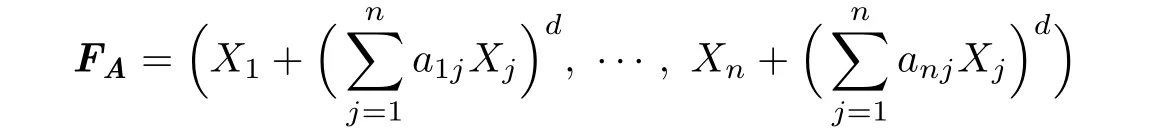
is called power linear of degree d,where A=(aij).In 1982,Bass et al.[2]showed that it suffices to investigate the Jacobian Conjecture for all cubic homogeneous maps,and in 1983, Dru˙zkowski[3]showed that it suffices to consider all cubic linear maps.

Gorni and Zampieri[4]introduced a notion of“pairing”between homogeneous maps and power linear maps(see Definition 2.1 below).The interest of the concept comes from that itestablishes connections between homogeneous maps and power linear maps,and preserves some important properties.In fact,a homogeneous map is invertible(tame,triangularizable, respectively)if and only if so is its Gorni-Zampieri pair(G-Z pair,for short)FA;see Section 6.2 of[5]for details and more such properties.

Due to the“pairing”,one may study the properties of a homogeneous map through its G-Z pair FA,and vice versa.For example,it was shown through G-Z pairs in[4],that CLLC (Meisters'cubic linear linearization conjecture)is equivalent to the DMZ-conjecture for cubic homogeneous maps,and then by use of this result,a counterexample to CLLC was obtained by Van den Essen in[6].Another example is the investigation of HDP(homogeneous dependence problem)and PLDP(dependence problem for power linear maps),which arise in the research of the Jacobian conjecture.HDP was proposed by several authors in 1990s,for example,see[7–8]or Section 7.1 of[1],which asks that,for a homogeneous map F=X+H with JH nilpotent,whether H1,···,Hnare linearly dependent over C?And PLDP asks if HDP has an affirmative answer for power linear maps,for example,see[9]or Chapter 6 of[5].Counterexamples to HDP(n,d)(where n and d denote the dimension and degree respectively)were given by De Bondt for every n≥5 with suitable d,including the ones for every n≥10 with d=3 and n≥6 with d=4,see[10]or Chapter 4 of[5].Counterexamples to PLDP were found by De Bondt for n=53,d=3,see Section 6.1 of[5],and independently by the authors in[9]for n=67,d=3.And in[9],connections between HDP and PLDP were established through G-Z pairs,and an algorithm was given to compute counterexamples to PLDP from those to HDP.

The G-Z pair is a useful tool in the research of some problems concerning polynomial maps.According to the construction for G-Z pairs in the original paper of Gorni and Zampieri[4],a function makePairing was given by Gorni in[11]for computing a G-Z pair of a homogeneous map.Unfortunately,the function makePairing is only valid for degree 3, and more crucially it may run into bugs sometimes,so there is a built-in check that should warn if the result is wrong.

In Section 2,we improve the algorithm and rewrite the function makePairing,such that it can not only guarantee the correctness but also be valid for degree 4.As an application, in Section 3,we give a function pldpExample(the function makePairing is called in this function)for computing counterexamples to PLDP from those to HDP,and by use of which some counterexamples to PLDP are obtained including one in the lowest dimension(n= 48)in all counterexamples to PLDP one has found up to now.All the codes(written in Mathematica 5.1)are given in Section 4.

2 G-Z Pairs

In what follows,we always view the vectors in Cnas column vectors,and write a polynomial map as F=(F1,···,Fn)T.Then a power linear map

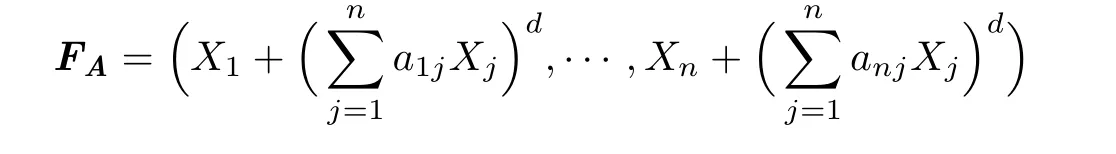
can be written as

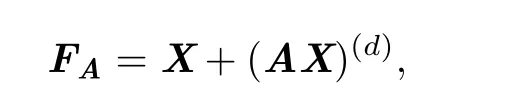
We recall the Definition and some basic properties of G-Z pairs;for details,see[4]or Section 6.4 of[1].

Definition 2.1Let f=X+H:Cn→Cnbe a homogeneous map of degree d≥2 and FA=Y+(AY)(d):CN→CNa power linear map with N＞n.We say that f and FAare paired through the matrices B∈Mn,N(C)and C∈MN,n(C)if

1.f(x)=BFA(Cx),x∈Cn;

2.BC=In;

3.kerB=kerA.

And FA(resp.f)is called a G-Z pair of f(resp.FA).

Remark 2.1The concept was originally introduced by Gorni and Zampieri[4]for d=3, which can be trivially generalized to every integer d≥2(cf.[9]).Note also that De Bondt introduced the so-called weakly G-Z pair,which generalizes the one above;see Definition 6.2.6 of[5].

One can see that,in Definition 2.1,

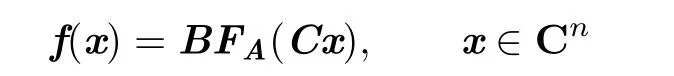
if and only if

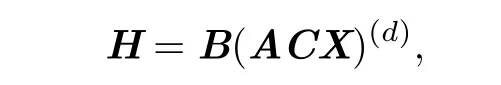
and the conditions BC=Inand kerB=kerA imply that

Every homogeneous map f in dimension n has a G-Z pair FAin dimension N＞n. Conversely,every power linear map FAin dimension N with n:=rankA＜N has a G-Z pair f in dimension n.

In what follows,we improve the algorithm and rewrite the function makePairing for computing a G-Z pair of a homogeneous map,such that it can guarantee the correctness and be more efficient than the old one.In addition,the revised function makePairing is also valid for degree 4.The improved algorithm is sketched in Table 2.1,and the correctness proof of which is given behind it.The code(written in Mathematica 5.1)of the improved function makePairing is given in Section 4.

Table 2.1

(continued)

The Correctness ProofBy Step 1,we have

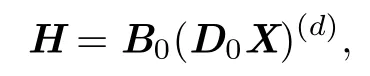
and by Step 2,we obtain that

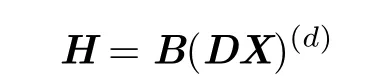
and

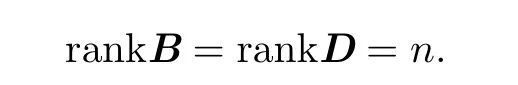
Since B has full row rank,there exists a matrix C such that

By Step 3,

which implies that

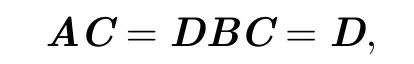
and thus

Since A=DB,we have

Noticing that

we have

Thus

Therefore,

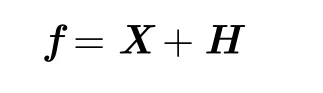
and FAis paired through the matrices B and C.

3 Counterexamples to PLDP

According to the algorithm given by the authors in[9],we give a function pldpExample for computing counterexamples to PLDP using those to HDP for degree 3 and 4,in which the function makePairing is called for computing the G-Z pair.The code is given in Section 4 In what follows,some new counterexamples to PLDP are obtained by use of the function pldpExample and the following counterexamples to HDP presented in Section 4.2 of[5].

Let n be even and let

where A and B are symbolic constants. Let

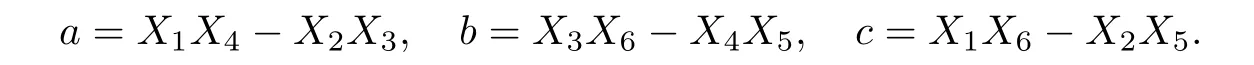
1.Take

Then f=X+H is a counterexample to HDP(9,3); 2.Take

Then f=X+H is a counterexample to HDP(9,3); 3.Take

Then f=X+H is a counterexample to HDP(6,4).

Taking f=X+H as 1,2 and 3 respectively,and calling the function pldpExample,we obtain counterexamples to PLDP(62,3),PLDP(58,3)and PLDP(48,4)respectively;see Table 3.1.

Table 3.1

(continued)

4 Functions

4.1An Improved Function for Computing the G-Z Pair

makePairing(f,d)

Input:a homogeneous polynomial map f=X+H and the degree d.

Output:a matrix A,such that FAis a G-Z pair of f.

<

Clear["‘*"];

Module[{dimension,var,toCombinition3,toCombinition4,recombined, monomialList,combinition List,temp,comb,b0,d0,b,d,a}, dimension=Length[Last[Homogeneous]];

var=Table[x[i],{i,dimension}];

If[dd==3,SetAttributes[toCombinition3,Listable];

recombined=toCombinition3[Evaluate[Expand[Homogeneous@@var-var]]],

If[dd==4,SetAttributes[toCombinition4,Listable];

recombined= toCombinition4[Evaluate[Expand[Homogeneous@@var-var]]],

Print["the degree is not 3 or 4."]]];

toCombinition3[0]:=0;

NumberQ[num]&&!NumberQ[a]&&!NumberQ[b]&&!NumberQ[c];

NumberQ[num]&&!NumberQ[a]&&!NumberQ[b]&&OrderedQ[{a,b}]; toCombinition3:=(num/6)*(a+b)^3-(num/ 6)*(b-a)^3-(num/3)*a^3/;

NumberQ[num]&&!NumberQ[a]&&!NumberQ[b]&&!OrderedQ[{a,b}]; toCombinition3:=num*a^3/;

NumberQ[num]&&!NumberQ[a];

toCombinition4[0]:=0;

NumberQ[num]&&!NumberQ[a]&&!NumberQ[b]&&!NumberQ[c]&&!NumberQ[d]; toCombinition4:=(num/6)*(a+b)^4-(num/ 6)*(a-b)^4-(num/48)*(2 a+b)^4+(num/48)*(2 a-b)^4/;

NumberQ[num]&&!NumberQ[a]&&!NumberQ[b]&&OrderedQ[{a,b}]; toCombinition4:=(num/6)*(b+a)^4-(num/ 6)*(b-a)^4-(num/48)*(b+2 a)^4+(num/48)*(b-2 a)^4/;

NumberQ[num]&&!NumberQ[a]&&!NumberQ[b]&&!OrderedQ[{a,b}]; toCombinition4:=-(num/6)*a^4-(num/6)*

b^4+(num/12)*(a+b)^4+(num/12)*(a-b)^4/;

NumberQ[num]&&!NumberQ[a]&&!NumberQ[b]&&OrderedQ[{a,b}]; toCombinition4:=-(num/6)*a^4-(num/6)*

b^4+(num/12)*(b+a)^4+(num/12)*(b-a)^4/;

NumberQ[num]&&!NumberQ[a]&&!NumberQ[b]&&!OrderedQ[{a,b}]; toCombinition4:=(num/ 48)*(a+b+c)^4+(num/48)*(a+b-c)^4-(num/ 48)*(a-b+c)^4-(num/48)*(a-b-c)^4-(num/ 24)*(a+b)^4+(num/24)*(a-b)^4/;

NumberQ[num]&&!NumberQ[a]&&!NumberQ[b]&&!

NumberQ[c]&&(OrderedQ[{a,c,b}]||OrderedQ[{a,b,c}]);

NumberQ[num]&&!NumberQ[a]&&!NumberQ[b]&&!

NumberQ[c]&&(OrderedQ[{c,b,a}]);

monomialList= Map[If[Head[#]===Plus,List@@#,{#}]&,recombined]//Flatten; combinitionList= Union[Select[monomialList,MatchQ[#1,(num_.)*(lin_)^dd]&]/. (num_.)*(lin_)^dd:>lin/;NumberQ[num]];

temp=recombined/.

Table[combinitionList[[i]]^dd->comb[i],{i,Length[combinitionList]}]; d0=Table[Coefficient[combinitionList[[i]],x[j]],{i, Length[combinitionList]},{j,dimension}];

b0=Table[Coefficient[temp[[i]],comb[j]],{i,dimension},{j, Length[combinitionList]}];

For[i=0,MatrixRank[b0]

d0=Join[d0,{Table[0,{dimension}]}]];

For[i=0,MatrixRank[d0]

b0=Transpose[Join[Transpose[b0],{Table[0,{dimension}]}]]];

b=b0;

d=d0;

a=d.b;

a];

4.2A Function for Computing Counterexamples to PLDP

pldpExample(f,d)

Input:A counterexample to HDP(n,d),f=X+H and the degree d.

Output:A list[n1,w],where n1 is a positive integer,and w is a matrix of n1 order,such that(wY)(d)is a counterexample to PLDP(n1,d).

a=makePairing[Homogeneous,dd];

s=Length[a];

m0=a.Transpose[a];

m=Transpose[Product[m0,{dd}]];

n1=MatrixRank[m];

q1=Transpose[RowReduce[m]];

r=Table[0,{n1}];

For[i=1;j=1,i<=s,i++,

If[TakeRows[q1,{i,i}]==TakeRows[IdentityMatrix[s],{j,j}], r=ReplacePart[r,i,j];

q1=ReplacePart[q1,0,{i,j}];j++]

];

p=q1+IdentityMatrix[s];

w1=a[[r,All]].p;

w=w1[[All,r]];

{n1,w}

];

[1]Van den Essen A.Polynomial Automorphisms and the Jacobian Conjecture.Progr.Math.vol. 190.Basel-Boston-Berlin:Birkh¨auser,2000.

[2]Bass H,Connel E,Wright D.The Jacobian conjecture:reduction of degree and formal expansion of the inverse.Bull.Amer.Math.Soc.,1982,7:287–330.

[3]Dru˙zkowski L M.An effective approach to Keller's Jacobian conjecture.Math.Ann.,1983, 264:303–313.

[4]Gorni G,Zampieri G.On cubic-linear polynomial mappings.Indag.Math.(N.S.),1997,8: 471–492.

[5]De Bondt M.Homogeneous Keller Maps.Ph.D.thesis.The Netherlands:Univ.of Nijmegen, 2009.

[6]Van den Essen A.A counterexample to Meisters'cubic-linear linearization conjecture.Indag. Math.(N.S.),1998,9:333–339.

[7]Meisters G.Polymorphisms conjugate to dilatations.In:Van den Essen A.Automorphisms of Affine Spaces.Dordrecht:Kluwer Academic Publishers,1995.

[8]Olech C.On the Markus-Yamabe stability conjecture.Proc.of the Intern.Meeting on Ordinary differential Equations and Their Applications.Florence:Univ.of Florence,1995:127–137.

[9]Liu D Y,Du X K,Sun X S.The linear dependence problem for power linear maps,Linear Algebra Appl.,2007,426:706–715.

[10]De Bondt M.Quasi-translations and counterexamples to the homogeneous dependence problem.Proc.Amer.Math.Soc.,2006,134:2849–2856.

[11]Gorni G.A Nonlinearizable Cubic-linear Mapping.In:Hubbers E.Conference on Polynomial Maps and the Jacobian Conjecture.Lincoln:Univ.of Nebraska-Lincoln,1997.

14R15,15A03

A

1674-5647(2013)04-0320-09

Received date:April 7,2011.

The“985 Project”and“211 Project”of Jilin University,the Basis Scientific Research Fund(200903286)of Ministry of Education of China,the NSF(11126044,11071097)of China,and Shandong Postdoctoral Science Foundation(201003054),Innovation Program.

E-mail address:liudayan@jlu.edu.cn(Liu D Y).