硼氢化钠水解制氢系统噪声特性研究

李大鹏

（海军工程大学，武汉 430033）

0 前言

隐蔽性是潜艇最为重要的战术性能。电化学发电机AIP潜艇使用NaBH4水解制氢要涉及到复杂的两相流动现象，在含有氢气-蒸汽气泡的NaBH4溶液两相流动以及气泡生长、浮升、融合、脱离等过程中，会有噪声产生，有必要研究其噪声特性，为降低两相流动噪声提供理论依据。

1 乳状液中的压力波传输

制氢器反应区内的两相混合物从结构上可分类为气体乳状液，其特征为含有气体、气泡尺寸分布离散上。气体成分包括水解过程中产生的H2、水蒸气、乙硼烷（B2H6）等，但 B2H6等气体在H2中含量不超过0.05%，可忽略对气泡水动力学特性的影响。使用确定蒸汽-气泡相间换热的导热积分方程解析解，对于有限幅度扰动，Δ p/ p ＜ 1，可将压力扰动方程组写成（1）、（2）式。

其中， ao=[kpo/(ρoϕo)]1/2-相间转换滞止音速；β=/(6ϕ )-气泡脉动与惯性效应有关的离散系数； m =3kpoρlcpl（dT / d p ）s/(ρgnr)-常数；v-无相变混合物气泡有效粘度； al-液体导温系数；ϕ-体积含气率； r-相变潜热。

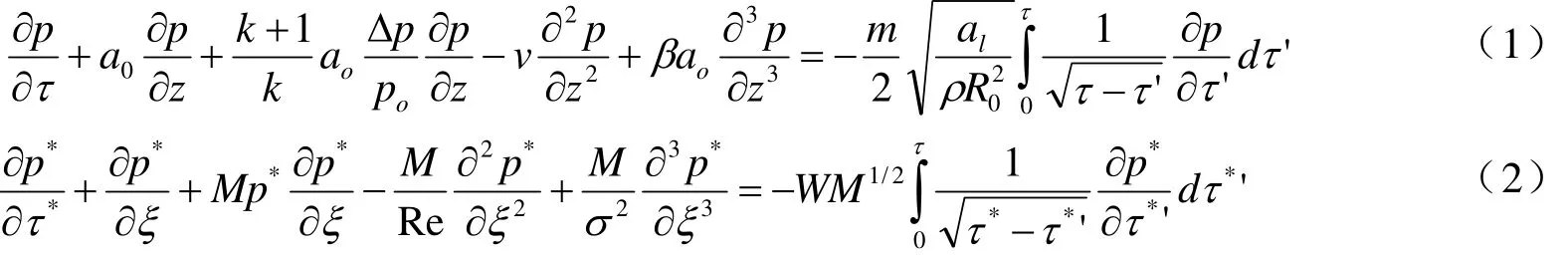
写成无因次形式，使用初始参数 Δp0为幅值，h0为长度，a0为特征速度。对于有限波长扰动，使用评价准则：1）σ=h0[(k + 1)Δp0/(2kp0β)]1/2， 定 义与 弥 散 效 应 相比，非线性效应波动截面的待求变量；2）W=m{kp0alh0/[2 πa0Δp0(k +1)]}1/2，表征相间换热和非线性效应的相对强弱；3）Re =(k+ 1)a0Δp0h0/(2kp0v)，表征无相变介质中耗散。对于冲击波类型扰动，使用定义相变和波的非线性扩张影响。当 W*或W较大时，状态具有相变特征，且当W→0时，波传播取决于非线性和惯性效应。与参数W有关，气泡介质中可能存在波束、单冲击波或振荡等多种结构[2]；4）M= uo/ao= (k +1)Δ po/(2kpo)，马赫数。H2管道上自动阀门突然关闭引起压力扰动按水力冲击处理[3]，有，其中中音速；ρ-H2密度； w0-到达阀门处的H2速度。

假设压力扰动冲击到达制氢器中蒸汽-气体乳状液边缘表面时没有发生变化。在气泡介质中，混合波结构由准则数 W*确定。 W*≥1的区域称为“热状态”区域，该区域内有限波长压力波混合时相间换热占主要影响。 W*＜0.1的区域称为“惯性状态”区域，该区域内有限波长压力波演变特征主要取决于准则数σ。其他准则数还包括仅由初始扰动形式定义的准则数σ*。当σ*>σ，气泡中为波束；当σ*<σ，气泡中为长波。冲击波可能是二重薄壁结构，呈单调（M<0.3）或振荡（M>0.3）变化。

ho≈ 4 Ro/为计算参数 W*和W，取使用参数：2.5 MPa压力下， R0=56，ϕo=0.28，扰动参数 Δp0=0.014 MPa，得到 h0=0.0056 m，W*=5.74 μm，即 W*＞1，所以扰动处于“热状态”区域。当 W*≥1时，气泡形成过程中的非线性和惯性效应不明显，将波的演变方程写成线性形式

对上式进行拉普拉斯变换，得到不同初始扰动下方程解。对于阶跃式初始扰动，有。利用概率积分函数和误差函数，将上式写成

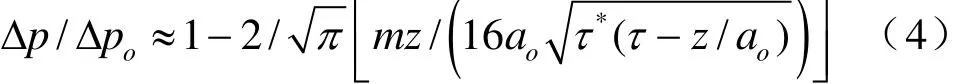
根据上面公式计算得到蒸汽-气体乳状液中波的演变过程见图 1。由图可见，波运动前沿被拉长。尽管0.7 m距离处波幅值减小，但所有幅值在经10 ms后都超过了初始幅值的80%。在“热状态”区域，蒸汽-气体乳状液中都不存在有冲击波和带有陡峭前沿的有限宽度区域，但幅值足够大，能够引起管道中流动振荡。另外，H2管道上阀门开启或关闭引起扰动也会造成两相流动波动。

2 气泡生长过程中的噪声

弹性介质中机械应力或局部压力发生改变的任何过程都可能产生声波。制氢器反应区中蒸汽-H2气泡的形成和生长将伴随有声能辐射。液相中压力波动频率和幅度取决于气泡生长速度。蒸汽-H2气泡生长缓慢。当汽、液相存在密度差时，气泡生长可能在液相中形成压力波。当汽、液相具有相同密度时，在气泡生长过程的任何时刻，系统处于平衡状态，气泡内部压力由液体静止压力和拉普拉斯方程确定的表面张力决定。汽、液相间密度差使得初始时刻由于存在质量交换，气泡中压力急剧增大，然后根据液体被排挤程度，压力开始下降并趋向于稳定，液体中因此出现惯性形成的过余压力。由于不均匀性增大，汽相中汽泡将发生波动，并在液相中产生正和负的压力波。

实际蒸汽相气泡生长不呈单调变化。列气泡压力方程时假设气泡压力变化为气泡生长和波动造成压力变化之和。如将蒸汽相气泡体积波动用谐波形式表示，气泡中过余压力变化写成

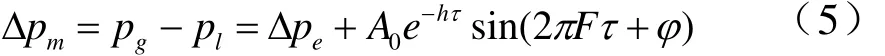
其中pg-气泡中蒸汽相压力； pl-液相静止压力；Δpe-液体惯性形成的气泡过余压力；Ao-压力波动的初始幅值；h-波动衰减系数；F-波动频率；ϕ-波动的初始相。

压力波动初始幅值应与气泡核心中蒸汽相压力Ao成正比，由临界半径表达式 Rc=2σ vo/Δϕ，得到 Ao= 2 kAσ /Rcr=kAvo/Δϕ，其中 kA为无因次比例系数，根据经验数据，kA= 2.0× 10-5ρl/ρg。气泡开始波动时，实际上液相中压力波动经过第一个周期后就开始衰减。经过一个循环后波动幅值减小，取 m =20，则衰减量 h =F ln(m/ n)= 3.0F，其中 n 为压力波动的循环数， n=1。

将上面相应表达式带入气泡过余压力变化表达式，得到

当气泡直径以指数规律增大到一定程度，等号右侧第二项可忽略。实际上气泡体积波动频率一般为几千Hz，可使用下式定义气泡自由波动频率[8]： Fo=（3k p∞/ρl）0.5/(2πRo)，其中 R0-气泡平均直径； p∞-对应气泡直径R0的液相静止压力；k-气体绝热指数。在制氢器反应区所处状态下，气泡直径255 μm，气泡自由波动频率61.8 kHz，由于粘性和质量交换的存在，实际值比计算值低。当液体中压力频率处于常见分布区间时，气泡生长产生压力pc=D( C∞- Co)ρl/(4ρgτ)。

假设所有 N个气泡都位于制氢器反应区内并作为等强度声源，则作用在制氢器壳体壁面上的声波强度

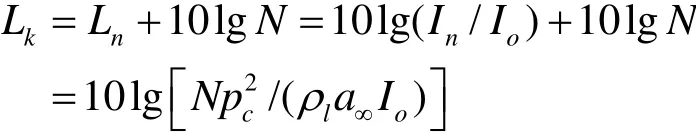
其中 Lk-作用在制氢器壳体总声波强度，db； Ln-气泡声波强度，db；In-单个气泡的声波强度，db；pc-气泡生长产生压力表达式定义的声压，Pa；a∞-液体中声波传播速度，m/s；Io-液体中声波强度 极 限 值 ， 为 2.66× 10-16W/m2， 气 体 中 为1.0× 10-12W/m2。将气泡生长产生压力表达式代入，得到

计算 Lk时使用了如下假设：蒸汽-气体乳状液中声波强力发散，且主要在气相体积中传播。其他参数取值： N=140000， ρl=1070 kg/m3，ka=1.5，C∞=100 kg/m3， D= 5× 10-9m/s，ρg=2.8kg/m3，τ=1 s，a∞=1500 m/s。带入计算，得到作用在制氢器壳体上声波强度仅为30 db。使用傅里叶积分变换确定水动力学噪声的幅频谱。导出上式时如下假设：所有气泡以同样幅值同步增大。实际上，制氢器反应区的某些位置上气泡增大情形要复杂些，此时液体中声压将是时间的非周期函数。声压谱密度可通过反向傅里叶积分关系式确定：

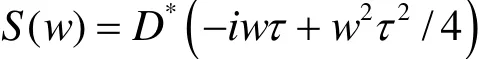
若已知声压谱密度，使用直接傅里叶变换并整理，得到

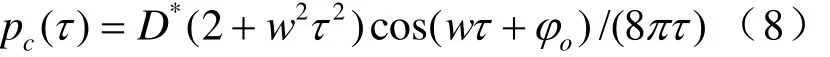
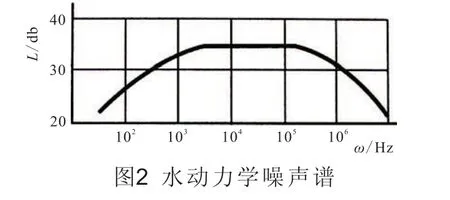
带入声波强度表达式，得到100～106Hz频率范围内作用在制氢器壳体上的总声波强度。计算得到的制氢器反应区中蒸汽-氢气气泡生长过程的水动力学噪声谱见图 2。可见，在 3～102kHz这一较宽频率区间内，曲线较为平坦，声波强度实际上保持不变。作用在制氢器壳体上的声波强度不大，约 35 db。这样的高频声波强度对于保证制氢器具有较高的声学性能是完全可以接受的。

3 气泡融合时的声能辐射特性

制氢器反应区内，蒸汽-气体气泡以不同速度浮升，期间会出现气泡融合，形成更大体积气泡，气泡的部分能量会转化为声能。

假设两个半径均为 R1的气泡融合，融合过程中，气泡中蒸汽-气体温度未发生改变，融合为等温过程。新气泡形成的主要条件是初始气泡与新形成气泡中的气体质量相等。使用克拉拍龙和拉普拉斯方程，可以得到新气泡半径:

当 2 σ/(R1ρl)≈2σ /(R2ρl)＜＜1时 ， 有R2≈ 1.26R1。融合时释放出能量：

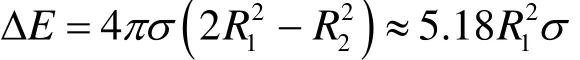
如果气泡融合发生在距离液面的一定位置处，则伴随融合还进行球状声波的变形过程。两个气泡融合时释放出的部分能量转变成声能，即

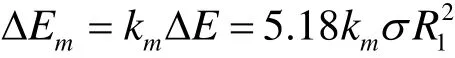
km为声波能量转换系数。声功率

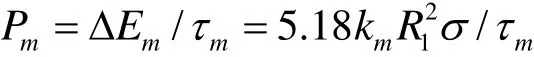
其中，τm-气泡融合时间。使用莱利公式得到τ =0.915R （ρ / p∞）0.5。假设气泡融合时间为生成半径为R2气泡所需时间，得到 τm=0.68 R （ρl/p∞）0.5。带入声功率表达式，得到

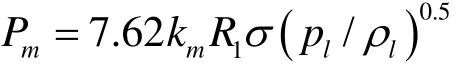
气泡融合时的辐射声能为气泡总势能的30%左右[6]。使用关系式 En/Es= Rp∞/(3σ)确定球状气泡势能与其表面能之比，两个气泡融合时的能量转换系 数 km=0.9σ /(R p∞)， 带 入 上 式 ， 得 到。由于气泡融合是在液、气相分界面上进行，空气中距离声源 r处的声波强度I=Pm/(4π r2)。声波强度水平LB=10 lg I/I0，其中Io=10-12W/m2。 距 离 制 氢 器 1 m处 ， 当pl= 2.5× 106Pa，计算得到声波强度为44 db。计算时水表面张力σ=0.05 N/m。实际上，制氢器反应区溶液中含有较强的表面活化剂 NaOH，会减小表面张力，并相应降低声波强度。

气泡融合强度不仅取决于表面活化剂，还与气泡尺寸有关。相邻气泡间距越大，融合所需接近距离就越小。乳状液中，可用融合速度不变的二阶反应方程描述:，其中No-初始时刻单位体积乳状液中气泡数目；Nτ-至τ时刻气泡融合数目。

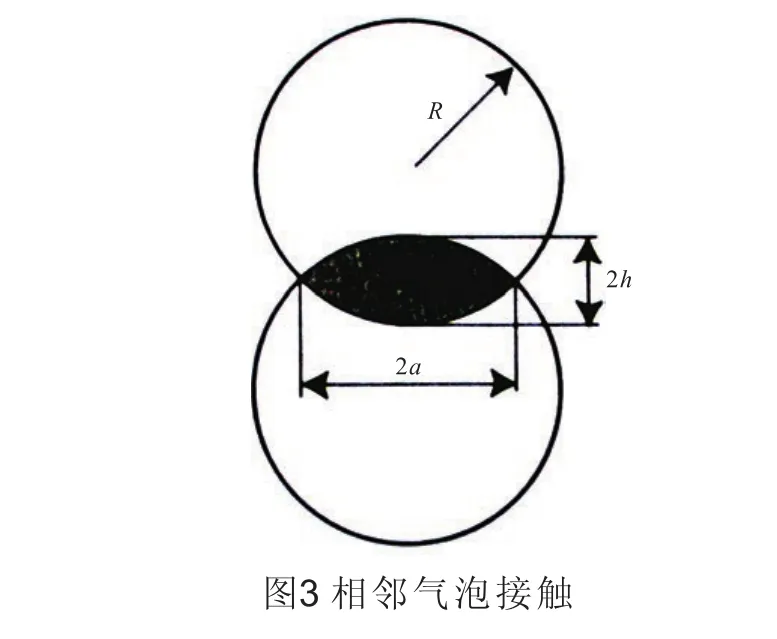
估算相互吸引靠近的两个气泡的声波强度时，假设接触位置处没有作为吸附层的分隔气泡存在，且气泡一直保持球状，气泡球心距离2 h，该距离与气泡球心间的初始距离 2 R相比可以忽略。见图3。由几何关系可知， R2= a2+ (R -h)2，且 h << R ，有 a2=2Rh。由于气泡接近，气泡表面能减小了 Δ Eσ=- 4πRhσ，相邻气泡间表面张力Fσ=-ΔEσ/h =-4πRh 。气泡间张力相当大。当R=250 μm，Fσ=1.57×10-4N，而作用在浮升气泡上挤出力 FAr=(4/3)πR3ρlg=6.87×10-7N，表面张力大大超过挤出力。气泡融合具有随机性，融合气泡数目及相应声脉冲数目须使用统计方法估算。假设1 s时间内，气泡融合数目服从正交对数分布规律，声脉冲平均数目可用下式估算：，其中 N-声脉冲最小数目，N=1；-声脉冲最大数目，等于气泡总数目一半，≈ 18000，得到声脉冲平均数目在130左右。距离制氢器 1 m处噪声强度LB,Σ= Ln,1+ 10lgmin=65。可见，气泡融合时的噪声强度比气泡生长形成时大得多。

气泡融合时可将声压作为过程参数的函数。对声脉冲压力进行傅里叶变化并整理，得到声能谱密度:

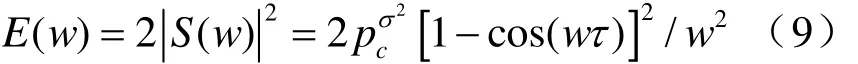
4 气泡脱离时的声能辐射特性

如气泡脱离时 30%能量转变为声能

声功率

距离声源r处的声波强度

在 r =1 m距离处声波强度 L= 10lg(I/Io)=82 db。制氢器噪声中最大的组成是液相表面的气泡脱离噪声。能辐射损失表达式未考虑与气泡脱离时形成液滴及液滴上升到一定高度等有关的能量损失，故计算值略高。但该式作为定性估算时是可信的。表面活化剂会降低溶液表面张力，会降低噪声水平。

对流体设备中空泡效应造成的空气噪声测量表明，仅有 0.01%左右的空化气泡功率会转化成声能。考虑声能耗散，气泡脱离液面造成声波强度

设自液面脱离的气泡半径均为 250 μm，有Ny个声脉冲源，气泡在0.2 m高度反应单元内的催化剂表面上生长。由气泡脱离直径表达式，计算得到的催化剂表面气泡脱离半径为 50μm。由气泡半径随时间变化表达式计算，气化核心产生并增大到50 μm半径气泡需时0.1 s，相邻气泡浮升1 mm。0.2 m高度反应单元内有200个气泡层，每个气泡层有190个左右气泡，液相上部跃离出液面的气泡数目 Ny=190，此时制氢器内气泡脱离液面造成的噪声强度= L + 10lg Ny= 42 +10lg190=65 db。气泡融合与气泡脱离产生的噪声强度相等。如果认为气泡声强度频率在200 kHz左右。

5 结束语

制氢过程涉及到气泡的形成和生长、浮升、运动等两相流动现象，制氢器内乳状液中压力波传输特性、气泡生长过程中噪声、气泡融合和脱离时声能辐射特性、声波传输速度的计算可基于已有的两相流动模型进行，并在此基础上，有针对性地从运行参数选择、制氢器设计等方面实施降噪。

：

[1]Nakorakov V.E., Schreiber I.R. Model of disturbances in the steam-fluid mixture[J]. TVT, 1979, 17 (4):798-803.

[2]Kutatelas S.S., Nakorakov V.E. Heat and mass transfer and wave in steam and fluid system[M]. Novosibirsk:Science, 1984.

[3]Sterenliht D. Hydrodynamics[M]. Moscow:Energoatomizdat, 1991.

[4]Nakorakov V.E., Pokusaev B.G., Schreiber I.R. Wave dynamics of gas and steam-fluid system environments[M]. Moscow: Energoatomizdat, 1990.

[5]Deadic A.N., Zamukov V.V., Deadic V.A. Ship air-independent power plants[M]. St. Petersburg:Shipbuilding, 2006.

[6]Miniovic I.R., Pernik A.D., Petrovsky V.S.Hydrodynamic sound sources[M]. Leningrad:Shipbuilding, 1972.