基于ANSYS／LS－DYNA的圆盘击水弹跳研究＊

陈诗伟

（中国船舶重工集团公司第七一○研究所 宜昌 443003）

1 引言

水上飞机的水面降落、返回舱的入水过程、民航客机的水面迫降以及空投航行器的忽扑行为等都涉及到跨介质运动，其主要特点在于物体近水面触浪滑跳飞行，发生二次击水，由于其特殊的运动方式，二战期间的滑跳攻击武器[1]以及近年来新提出的高效突防武器—跨介质飞行器，都是以此为基础的，因此文章从简单物理现象出发，利用数值仿真的方法，着重研究产生滑跳的原因以及实现多次滑跳的条件。

本文利用LS－DYNA的ALE方法对圆盘击水滑跳现象进行三维数值仿真，并与C.Clanet，F.Hersen，and L.Bocquet[2]做的试验结果进行对比，旨在利用仿真手段对这一特殊现象进行一个初探。

2 数值仿真模型及算法

根据流体力学的原理，流速越大压强越小。当物体（密度比水大）掠过水面时，带动它下面的水在非常短的时间内快速流动，从而压强减小，而更下面的水是静止不动的，产生的压强大，如此就对物体产生一个压力，当压力大于物体的重力时，物体就会弹起，这样的情况重复多次，物体就会出现在水面上跳跃的情况。当压力小于重力时，物体就沉入水中。此外，当物体旋转时，能更加带动水的流动，跳跃的次数会更多。图1为圆盘击水滑跳示意图。

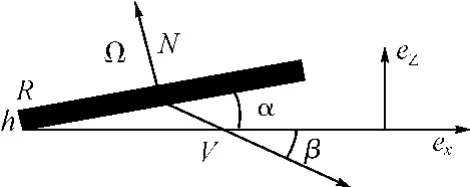
图1 圆盘与水面碰撞过程示意图

其中，圆盘质量M，初始速度V，角速度Ω，倾角α，入水角β，沾湿表面积Sim，圆盘的半径和厚度R和h。

图2 圆盘击水计算网格

以C.Clanet，F.Hersen，and L.Bocquet所做的实验，圆盘直径D＝5cm，厚度h＝2.75mm。其中，圆盘没在空气中，空气和水的边界采用的是无反射边界，空气和水的接触面采用的是共节点。圆盘虽然是从一个较高的地方冲击水面，但是我们在模拟的时候不需要将圆盘的初始位置定的很高，因为这样就增加了不必要的求解时间。圆盘击水的有限元模型如图2所示，在流固耦合交界面上采用加密网格处理。本文选用m－kg－s单位制。

为了简化计算模型，圆盘采用刚性材料，圆盘在整个击水过程中不发生形变，在算法的选择上：刚性体选用的是Lagrange算法，空气和水选用的是Euler算法，圆盘和水之间采用的是耦合算法。

在流体和结构相互作用问题中，流体的运动幅度比较大。在流体和结构交界面上的每个点处需设置两个节点，即流体节点和结构节点[3]。其中：V1和V2为网格点速度，V′1和V′2为物质点速度。

固体节点应满足物质表面条件

在涉及到流体流动时，为了既能准确描述流体的边界，又能维持网格的合理形状，一般只在流体表面的法向方向上使用物质描述，而允许网格沿切向运动。即

式中：nx和nε分别是物体的现时构形和参考构形的表面外法向矢量，上式需要在自由表面上求解以确定自由表面的位置。

对于流体和结构相互作用问题。在交界面上和物体可以沿切向滑动、相互粘接或相互脱离。如果二者完全粘接，则界面上节点对物质速度应相等。即

如果两物体沿界面的切向滑移，则界面上节点对的法向物质速度应相等，即

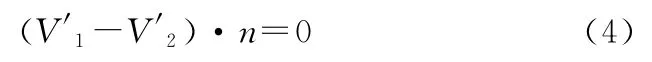
式中：n为界面的法向矢量。

如果两物体相互脱离，则界面上节点对的物质速度是相互独立的。计算网格的选取独立于物体自身的运动。因此可令界面上节点对的网格运动速度相等，使得界面上的节点在变形过程中始终保持重合，以简化流体－结构相互作用问题中界面的处理过程。

总之，在整个变形过程中，在流体和结构交界面上流体质点不能穿越网格，而且也不能穿越固体表面，同时应使固体网格点和流体网格点在界面上始终保持重合[5]。

3 材料模型和状态方程

在材料模型的选择上，空气和水采用的是LS－DYNA提供的MAT＿NULL流体空模型。在状态方程的选择上，空气和水都采用的是Gruneisen状态方程[6]。

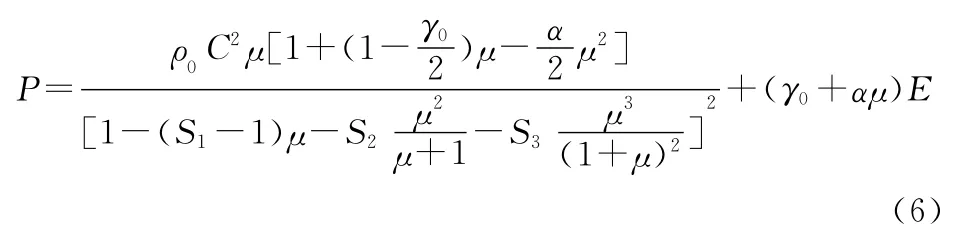
式中：C、a、S1、S2和S3是与材料冲击压缩特性有关的常数。C是us－up（冲击波速度—质点速度）曲线的截距；S1、S2和S3是us－up曲线斜率的系数；a是对Gruneisen系数的一阶体积修正；γ0是Grüneisen系数；E为材料内能；μ为水密度变化率。材料状态方程参数见表1。

表1 水和空气的状态参数

4 计算结果

圆盘击水是否发生滑跳有以下几个影响因素：入水速度V、入水角β、初始倾角α、旋转角速度Ω。本节主要对不同工况进行仿真计算，同时与相应的试验和理论结果对比，旨在验证数值方法的有效性。

4.1 倾角与最小入水角

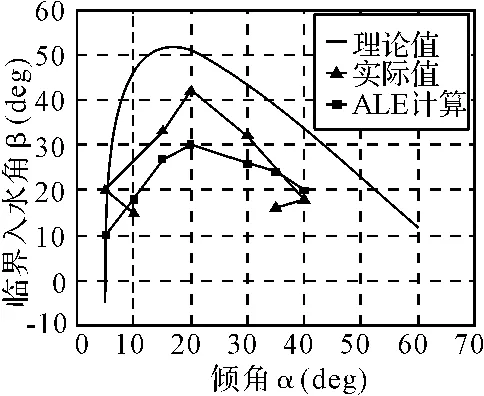
图3 倾角与入水角的关系

为了研究倾角与最小入水角之间的关系，根据文献资料，这里固定圆盘的入水速度V＝3.5m／s，角 速 度Ω＝65rot／s时，ALE仿真结果和理论计算以及试验对比给出在图3中。

从上图可以看出，数值结果曲线、实验曲线以及理论结果曲线走势基本相同，数值计算的结果比实验值偏小，而理论计算值更大。原因是，数值计算中选取的流体状态方程参数与试验时候的实际流体（空气、水）的状态不一致，这里采用的是某一时态的参量值，难免有一定的差异。理论计算过程中没有考虑入水空泡，并且进行一系列简化处理。所以采用ANSYS／LS－DYNA在进行击水滑跳分析时也作了相应简化处理，但与实际情况差别不大。

4.2 倾角与最小速度

用同样的方法研究入水速度和倾角的关系，固定入水角β＝20°，角速度Ω＝65rot／s时，ALE仿真结果和理论计算以及试验对比如图4所示。

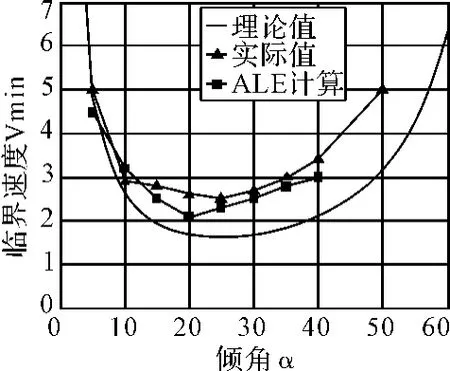
图4 圆盘倾角和最小速度的关系

从上图中不难发现，圆盘最小速度和倾角呈一包络曲线，ALE方法可以和试验以及理论值很好地吻合，当倾角过小或者太大时，无论多大的速度都无法使圆盘发生滑跳，同时，圆盘在20°左右存在一个最佳倾角，在这个角度下圆盘需要最小的速度就可以实现滑跳，这与L.Bocquet等人所做的试验可以很好的吻合。图5和图6分别给出了在α＝20o、β＝20°、V＝3.5m／s、Ω＝65rot／s时，圆盘击水滑跳的试验图片和数值仿真图片，可以看出运用ALE法可以较准确的模拟出圆盘滑跳过程。

图7给出了在α＝20°、β＝20°、V＝1.5m／s、Ω＝65rot／s时，圆盘击水仿真图。从图中可以看出，由于速度过小圆盘无法成功滑跳，但是圆盘仍然可以保持一定的姿态，没有立即翻倒下沉，这是由于旋转稳定的作用，即陀螺效应。这一效应将在下一小节给出讨论。

图5 圆盘击水滑跳试验图

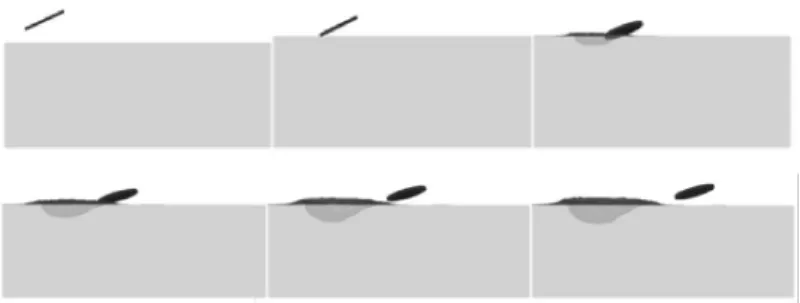
图6 圆盘击水滑跳仿真图

图7 圆盘击水滑跳仿真图

4.3 陀螺效应

旋转速度在整个滑跳过程中起着至关重要的作用，尤其是它对倾角α的稳定作用，如图8所示，当Ω＝0，即圆盘不旋转的时候，在击水过程中，圆盘将翻倒，紧接着沉入水中。因此，旋转的主要作用是：在击水滑跳的过程中稳定圆盘姿态，也就是L.Bocquet提出的陀螺效应[7]。

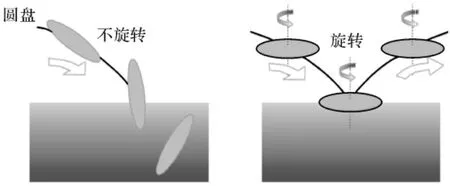
图8 旋转对击水滑跳的影响示意图

图9 圆盘（Ω＝0）击水滑跳试验图

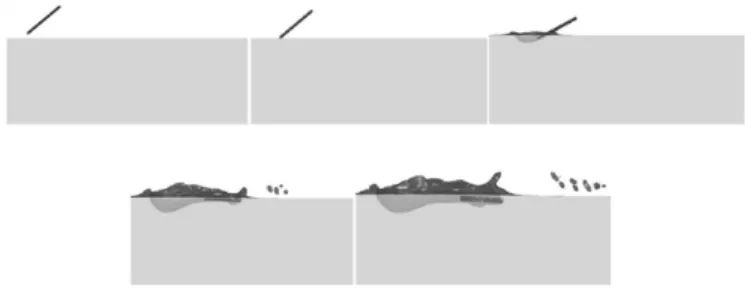
图10 圆盘（Ω＝0）击水滑跳仿真图

图9和图10给出了在V＝3.5m／s、α＝35°、β＝20°、Ω＝0时圆盘击水滑跳的试验图和仿真图，从图中容易看出，在击水过程中，由于圆盘没有旋转，它无法稳定运动姿态，此时，圆盘将翻倒，紧接着沉入水中。仿真图可以与试验取得很好的一致，图10中圆盘的姿态和图7形成对比。

5 结语

利用显式积分有限元软件LS－DYNA的ALE方法对气／液两相跨介质运动进行了初步研究，用该方法建立了圆盘在水和空气中运动的有限元模型，计算结果和试验可以很好的吻合，结果表明所建模型是可行的，采用的方法是合理的，为研究跨介质运动提供了一条有效的途径。该模型可用于物体在气／液两相流中运动特性以及入水冲击过程的联合分析。

[1]http：／／www.stoneskippi ng.com ＆ http：／／www.yeeha.net／nassa／guin／g2.html[OL]

[2]Rosellini，L.，Hersen，F.，Clanet，C.et al.（2005）Skipping Stones[J].Journal of Fluid Mechanics，543，137－146.

[3]时党勇，李裕春，张胜民.基于 ANSYS／LS－DYNA8.1进行显式动力分析[M].北京：清华大学出版社，2004：12.

[4]常秀丰，路明，张戎，等.基于ANSYS／LS－DYNA的多点起爆网络设计与研究[J].计算机与数字工程，2009（10）.

[5]J.O.Hallquist.LS－DYNATheoretical Manual[M].Livermore Software Technology Corporation，Livermore，California，2006.

[6]J.O.Hallquist.LS－DYNA user＇s manual v970[M].Livermore Software Technology Company，Livermore，2004.

[7]L.Bocquet.The Physics of stone skipping[J].Am.J.Phys.71，150（2003）.