打击核电厂目标的毁伤指标分析＊

詹仁超 李应岐 翟龙刚

（第二炮兵工程大学 西安 710025）

1 引言

由于现代社会对能源的需求持续增加，核电对世界的发展越来越占据着重要的作用，加之核电厂具有的放射性，打击核电厂必然成为战争时被攻击的重点。在打击核电厂的同时，需要进行毁伤效果评估。由于核电厂目标的特殊性，可将毁伤效果评估分为两步进行，即功能毁伤评估和核辐射安全评估。功能毁伤评估的主要任务是对打击目标执行预定任务的功能或作战能力的损毁情况进行定性评估。通过分析目标的结构与工作流程，确定关键子部件，根据物理毁伤评估的结论，将打击目标现状与初始目标进行比较，从而确定目标功能发生的变化。核辐射安全评估的主要任务是在打击核电厂目标后，根据核反应堆堆芯溶化与安全壳完整性失效的结论，判断核电厂周围放射性物质的释放量以及居民全身和甲状腺所接受的辐射剂量是否超过允许的规定值。

要对打击核电厂目标进行毁伤效果评估，就必须首先构建核电厂功能毁伤程度的指标体系与核电厂辐射程度的指标体系。

2 核电厂目标毁伤指标体系组成

2.1 功能毁伤指标

目标功能的毁伤程度是实战中攻击方最为关注的问题，而目标是否能完成特定环境下的任务使命，却是防御方最为关心的问题。因此，在选取目标的功能毁伤指标时，应综合考虑己方的作战意图和对方目标的任务使命。

核电厂的整体毁伤程度可以从三个角度来衡量：发电能力、修复时间和供电可靠性。而发电能力的度量为剩余容量比或损失容量比；可靠性的度量为输出电力期望和供电有效度。

这些指标中，发电能力指标反映了己方打击电厂的作战意图，修复时间指标体现了电厂功能下降持续的时间，而供电可靠性指标则反映了电厂目标使命任务（供电）的实现情况。

2.2 辐射程度指标

在对核电厂进行打击后，我们需要评估核电厂放射性物质是否泄漏。当核电厂功能毁伤程度指标达到攻击方要求的同时，能成功避免放射性物质泄漏是攻击方最愿意接受的。因为放射性物质一旦大量向外泄漏，受害方不仅仅是被攻击方，也可能是攻击方或者其他地区，大大加大了国际舆论的压力，所以攻击方必须对打击核电厂后核辐射程度做全面的评估。

为了便于建立模型，我们可以用两个指标来度量核辐射程度：放射性核素释放量指标与放射性物质在环境中的溶度指标。需要注意的是上述两个指标是建立在核反应堆堆芯溶化与安全壳完整性失效的前提下而提出的。核电厂目标毁伤指标体系如图1所示。

图1 核电厂毁伤指标体系

3 核电厂目标毁伤指标分析

3.1 基于电厂发电能力下降程度的指标

度量电厂发电能力的指标主要有装机容量（Installed Capacity）、剩余发电容量（Left Capacity）和损失容量（Destroyed Capacity）[1]。

电厂发电能力可以分为两个层次：一是单个机组的发电能力，二是电厂整体的发电能力。对于一台机组有如下关系：

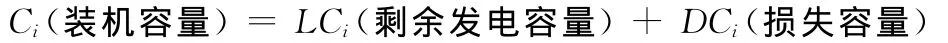
对于一个发电厂有如下关系：

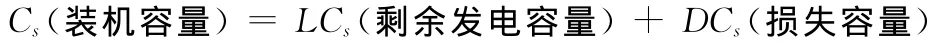
因此，可以将电厂整体剩余发电容量与装机容量的比值、损失容量与装机容量的比值作为度量其发电能力下降程度的功能毁伤指标，分别称为剩余容量比和损失容量比：

将剩余容量比与损失容量比[2]统称为发电能力指标。

作战时，由于电厂子目标毁伤状态的判断具有不确定性，所以计算得出的发电能力指标也具有随机性，LRs是一个随机变量。对于计入这种概率因素，有三种解决方案（以剩余容量比为例）：

1）以剩余容量比的数学期望E（LRs）作为功能毁伤指标；

2）以剩余容量比小于某阈值LRs0的概率P（LRs＜LRs0）作为功能毁伤指标；

3）以置信度为1－α的剩余容量比上限值LRsα作为功能毁伤指标，即要求P（LRs＜LRsα）＝1－α。

3.2 基于电厂修复时间的指标

从作战的角度来看，打击者不仅关心打击后目标的能力下降情况，更关心其功能降低或失效的持续时间。这个时间从目标的角度来看，就是修复时间。修复时间的大小对下一步的作战决策甚至作战进程都会产生影响。对于电厂目标，发电功能失效一小时与失效一星期的意义是完全不同的，有时甚至能决定战争的胜负。因此，修复时间也是衡量电厂功能毁伤程度的重要指标之一。

电厂的修复时间取决于其设备的损坏数量、损坏程度、有无备件以及维修工人数量等等。将备件、维修人员等统称为修复资源。电厂修复时间的长短由目标的毁伤状态和修复资源二者同时决定。

作战时，由于子目标毁伤状态的判断具有不确定性，所以计算得出的修复时间也具有随机性。将修复时间记为随机变量T。对于计入这种概率因素，同样有三种解决方案：

1）以修复时间的数学期望E（T）作为功能毁伤指标；

2）以修复时间大于某阈值T0的概率P（T＞T0）作为功能毁伤指标；

3）以置信度为1－α的电厂修复时间下限值Tα作为功能毁伤指标，即要求P（T≥Tα）＝1－α。

3.3 基于电厂供电可靠性的指标

对电厂打击后，可能会造成电厂自身发电能力的下降，但不一定会对电厂向外界供电的功能产生大的影响，因为电厂的发电机组一般都有一定的备用裕度，在能够满足一般负荷需求的基础上另设有备用设备与机组[5]。此时由于电厂整体备用裕度的下降以及电厂子目标本身的故障率，电厂供电的可靠性会下降。首先介绍电厂可靠性评估中几个常用的概念[5]。

电厂整体的可用发电容量是指考虑子目标故障率时电厂在能够持续输出的最大容量，记为ACs。电厂整体的停运容量是指考虑子目标故障率不能连续带负荷的容量，记为OCs。

根据以上定义，对于一台机组有如下关系：

LCi（剩余发电容量）＝ACi（可用发电容量）＋OCi（停运容量）

对于一个发电厂有如下关系：

LCs（剩余发电容量）＝ACs（可用发电容量）＋OCs（停运容量）

一般地，设某电厂遭受打击后的剩余发电容量为LCs，电厂停运容量为OCs1，OCs2，…，OCsn的概率是p1，p2，…，pn。将停运容量与对应的概率制成表格如表1，该表称为容量停运概率表[2]。

表1 容量停运概率表

由容量停运概率表可以计算得到两个可靠性指标：电厂的可用发电容量期望、电厂供电有效度。

1）电厂的可用发电容量期望

电厂的输出电力期望ECs为

输出电力期望表示电厂能够平均输出的电力。

2）电厂供电有效度

电厂的供电有效度即它满足用户要求的程度，这里定义为输出电力满足用户最低负荷需求的概率[1，6]。假设某一短期时间内，电厂的最低负荷为一定值M，若电厂所有状态中可用发电容量不小于M的容量状态为ACs1，ACs2，…，ACsk，则电厂的有效度定义为

作战时，由于电厂子目标毁伤状态的判断具有不确定性，所以计算得出的可靠性指标大小也具有随机性。对于计入这种概率因素，同样有三种解决方案（以电厂供电有效度为例）：

1）以电厂供电有效度的数学期望E（Pval）作为功能毁伤指标；

2）以电厂供电有效度小于某阈值Pval0的概率P（Pval＜Pval0）作为功能毁伤指标；

3）以置信度为1－α的电厂有效度上限值Pvalα作为功能毁伤指标，即要求P（Pval≤Pvalα）＝1－α。

3.4 放射性核素释放量指标

放射性物质由主回路进入安全壳以后，一般是以气体或悬浮的气溶胶形态存在于安全壳空间中。要计算出放射性物质从安全壳向环境的释放量，首先要计算其释放率，即为放射性浓度和安全壳体积泄漏率的乘积[7]。为了便于建立模型，假设安全壳内气体始终充分混合，放射性物质浓度是均匀的，则有：

其中：C（t）为放射性核素的浓度；（t）为主回路系统向安全壳是释放率；Vct为安全壳体积；λ＊为因安全壳泄漏引起的放射性减弱常数；λ为放射性衰变常数；λ为放射性去除常数。

对于各类核素：

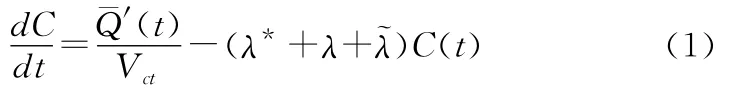
其中：Fct为安全壳的体积泄漏率。

假设在t＝0时，由主回路瞬时向安全壳释放放射性物质，其余时间无释放，则方程解为

放射性物质从安全壳向环境的释放率即为放射性浓度和安全壳体积泄漏率的乘积。

由事件开始到时间t，总共向环境释放放射性物质的累积总量为

将式（3），（4）代入，由此可求出Q（t），得

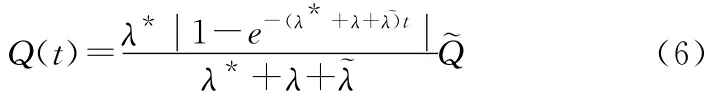
3.5 放射性物质在环境中的溶度指标

放射性物质一般呈气体或者气溶胶形态从安全壳释放到大气层中，我们统称这两种形态物为气载物。这些气载物进入大气后，在被风朝向下风向输送的同时，将受大气湍流影响，于水平和垂直方向迅速地稀释扩散。要估算放射性释出物对居民的辐射后果，首先必须研究气载物的在大气的稀释扩散规律，以计算居民所在处地面空气中放射性浓度X。

为了便于建立模型，我们采用半经验的高斯烟云扩散模型（正态分布模型）来描写气载物在大气中的稀释扩散规律[7]。

假设有一个距地面高度为h均匀连续排放源A。x轴沿平均风向向水平延伸，y轴在水平上垂直于x轴，z轴垂直向上，原点o在排放源点A的垂直地面处。在平坦的地形条件下，当大气中垂直温度梯度均匀，方向没有不连续变化时，可以假设气载物的浓度在下风向的每一位置处，横风方向和垂直方向的分布都是对称分布。假设气载物顺风移动时既没有从烟云中消失，也没有增加，则气载物应满足连续条件

由连续条件及加上所假设的对称性，即能解得气载物在大气中的浓度分布的正态模型

其中：Q′为均匀连续排放源的排放率；X为在（x，y，z）处空气中放射性的浓度为平均风速；σy，σz分别为y方向和z方向的扩散系数，它随天气类型而变化，也是X的函数。

若地面对气载物不吸收，而仅起全反射作用，则地面的作用相当于在（0，0，－h）处有一个像源。此时有

当z＝0，h＝0时，则地面排放源造成的地面浓度为

3.6 核电厂毁伤评估流程

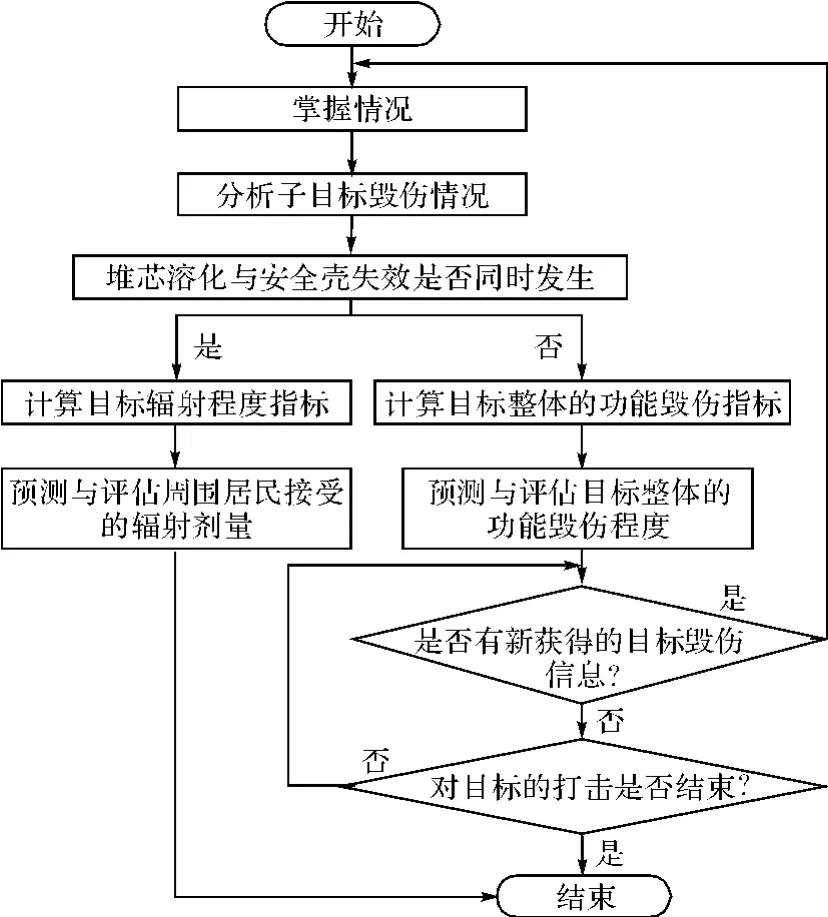
图2 核电厂毁伤评估流程

在评估核电厂目标毁伤程度时，我们可以将核电厂分成各个子目标的集合体，根据各子目标的毁伤数据，建立模型计算核电厂目标毁伤指标，而后预测与评估目标整体的毁伤程度。需要注意的是当核反应堆堆芯溶化与安全壳完整性失效同时发生时，表明该核电厂已经不具有发电能力，只需预测与评估核辐射的影响程度。核电厂毁伤评估流程如图2所示。

4 结语

打击核电厂目标的毁伤效果指标分析对于打击核电厂目标毁伤效果评估具有重要的意义，也是其核心内容，为打击核电厂目标毁伤效果评估模型打下了铺垫。由于篇幅所限，对于打击核电厂目标的毁伤效果指标建模以及计算方法将在以后进行讨论。

[1]唐小波，李天然，钱旭盛.变电所运行与管理[M].北京：化学工业出版社，2008.

[2]郭永基.电力系统可靠性分析[M].北京：清华大学出版社，2003.

[3]房晔，徐建.发电系统可靠性分析原理和方法[M].北京：中国电力出版社，2009.

[4]Bailey T M.The Role of Doctrine in Efective Combat Assessment Maxwell Air Force Base[J].Assess for Success，Alabama，2001（4）：23－25.

[5]周家启，任震，译.电力系统可靠性评估[M].重庆：科学技术文献出版社重庆分社，1984.

[6]南京工学院.电力系统[M].南京：电力工业出版社，1979.

[7]朱继洲.核反应堆安全分析[M].西安：西安交通大学出版社，2004.

[8]施仲齐.核电的环境影响[M].北京：原子能出版社，1994.

[9]Bailey T M.The Role of Doctrine in Efective Combat Assessment Maxwell Air Force Base[J].Assess for Success，Alabama，2001（4）：23－25.

[10]李新其，杨世荣，李小强，等.基于功能易损性的指标选取[J].弹箭与制导学报，2005，25（4）：702－705.

[11]尤晓建.基于目标识别的机场跑道打击效果评估研究[J].计算机与数字工程，2010（10）.

[12]Kilgalon J M.Operational Fires Did rI1Iey Achieve Maximum Efects during the GulfWar[J].Naval War College，2001（2）：16－18.

[13]Courtney P.Use of National Imagery Intelligence Assets to Obtain Battle Damage Assessment of Tactical Battlefield Targets[J].Naval War Colege，2001（2）：41－46.