截流钢筋笼的稳定性及其计算方法

李学海，程子兵，汪世鹏，石教豪

（长江科学院a．水力学研究所；b．武汉长科工程建设监理有限责任公司，武汉 430010）

式中：γs为钢筋笼的重度，g为重力加速度。

3．1．2 扁度系数λ的引入

在泥沙起动流速公式中，通常采用扁度系数λ的指数形式对卵石的起动流速进行修正，指数通常取1／3～1／2［2］，韩其为院士取0．45［3］。本文依据试验成果，将前述不同形状六面体钢筋笼稳定试验中得出的各工况正六面体的稳定系数均值作为拟合标准进行拟合。

（1）止动流速计算时，将各种扁度钢筋笼的止动稳定系数除以λ1／2，再进行平均，得出的稳定系数均值与正六面体止动稳定系数基本吻合，得到光滑面钢筋笼止动流速计算公式为

截流钢筋笼的稳定性及其计算方法

李学海a，程子兵a，汪世鹏b，石教豪a

（长江科学院a．水力学研究所；b．武汉长科工程建设监理有限责任公司，武汉 430010）

对实践中常用到的正六面体钢筋笼的稳定性从质量、形状以及有无垫底材料等方面进行了试验研究及工程实例验证。首次拟合提出了考虑其形状因素、河床糙度因素的正六面体钢筋笼止动流速和起动流速的计算公式，经试验验证具有较高的计算精度和实用性。此外，对四面体钢筋笼的稳定性也进行了试验研究，研究表明：四面体钢筋笼用于截流抛投这类止动问题的工程时，其止动稳定性明显优于相同质量的正六面体钢筋笼；而对于护底等起动问题的工程，两者起动稳定性差别不大。

截流；六面体钢筋笼；四面体钢筋笼；稳定特性；影响因素；计算公式

1 研究背景

在水利水电工程建设中，人工块体作为截流抛投材料或护岸材料已得到广泛应用。人工块体大致分为2类：一类是混凝土块体，如四面体、实心六面体、空心六面体、多角体、扭工字体、扭王体等，其中四面体由于其稳定性能较好，且在有无覆盖层及护底条件下适应性较佳，常应用在截流工程中，空心六面体因形状规则、透水性好而广泛应用于护岸工程；多角体、扭Ⅰ字体、扭王字体易于相互咬合，常用于海岸工程和大江大河工程岸坡防护中。另一类是天然石料集合体，如钢筋笼、合金笼网兜等。由于天然中小石料在现场易于获得，将其装在一起构成整体以后，增大了单个块体的质量，并具有良好透水性，其抗冲能力明显高于现场天然石料，且制作加工简单，在截流工程和护岸工程中均得到了广泛应用。然而，到目前为止，未见有关钢筋笼及合金笼网兜稳定性及计算方法的研究成果。基于此，本文对作为截流抛投材料的钢筋笼块体的稳定性及计算方法进行了研究。

2 六面体钢筋笼的稳定性试验研究

试验在1∶60比尺水槽中进行。试验分Q＝50，75，100 L／s 3级模型流量进行了止动和起动试验。止动试验按以下程序进行：各级流量下，保持流量不变，通过尾门调节下游水位，在试验段抛投试验块体，如稳定，微调下游水位，直至抛投块体部分流失、部分滑动一段又能稳定下来为止。起动试验按以下程序进行：各级流量下，保持流量不变，预先将试验块体放置在试验段底板上，通过尾门调节下游水位，直至试验块体开始滑动，且滑动速度较慢，直至部分块体滑动一段又能稳定下来为止。在止动和起动试验过程中，均测量试验段水深及垂线流速分布。

2．1 不同质量的六面体钢筋笼稳定性比较

选取了7种不同尺寸的正方体钢筋笼，其整体重度均采用19．6 kN／m3，对应于原型质量为2．00～31．25 t。

2．1．1 光滑水泥面上

采用伊兹巴斯公式［1］计算得光滑水泥面上不同质量的正方体钢筋笼稳定系数，计算结果参见表1。试验结果表明：质量为2．00～31．25 t正方体钢筋笼的临界起动流速均值约为临界止动流速均值的1．37倍，其止动稳定系数K止动值范围为0．52～0．74，均值为0．59；其起动稳定系数K起动值范围为0．71～1．12，均值为0．81；临界止动流速和临界起动流速均随块体质量增加而增大，而止动稳定系数和起动稳定系数均随块体质量的增大而减小。

2．1．2 Δ＝0．3 m石料垫底

Δ＝0．3 m（原型，Δ为垫底石料化引成球体的化引直径）石料垫底情况下，不同质量的正方体钢筋笼稳定系数计算结果见表2。试验结果表明：质量为2．00～31．25 t正方体钢筋笼的临界起动流速均值约为临界止动流速均值的1．33倍，其止动稳定系数K止动值范围为0．62～0．95，均值为0．75；其起动稳定系数K起动值范围为0．89～1．18，均值为1．00。临界止动流速随块体质量变化不明显，而在块体质量大于6．75 t后，临界起动流速随块体质量增加而增大的趋势明显；止动稳定系数和起动稳定系数均随块体质量的增大而减小。

2．2 不同形状六面体钢筋笼稳定性比较

本节中考虑了六面体钢筋笼2种方式的体型变化。令六面体钢筋笼的长轴、中轴、短轴长度分别为a，b，c，则扁度系数的六面体钢筋笼，在a＝b＝c时为正六面体钢筋笼；在a＞b＞c时为条形钢筋笼；在a＝b＞c时为扁钢筋笼。试验采用整体重度为19．6 kN／m3，对应于原型质量16 t的条形钢筋笼和扁钢筋笼进行比较，保持体积及质量与16 t正六面体一致。

2．2．1 条形钢筋笼

光滑水泥面上不同扁度系数的条形钢筋笼的止动和起动试验结果表明：条形钢筋笼的止动稳定与抛投方式无关，因为无论长轴垂直流向抛投还是顺流向抛投，块体入水后，最后均会变成长轴顺流向落到底板上。条形钢筋笼的止动稳定系数K值范围为0．52～0．75，均值为0．69；临界止动流速和止动稳定系数均随扁度系数λ的增大而增大。条形钢筋笼的起动稳定则与块体摆放的方式有关，长轴顺流向放置时的稳定性明显高于垂直于流向放置时。长轴顺流向放置时起动稳定系数K起动的均值为0．94，垂直流向放置时起动稳定系数K起动的均值为0．83。长轴顺流向放置时条形钢筋笼起动稳定系数K起动值随扁度系数λ变化差异不显著，而长轴垂直流向放置时K起动值则表现为随扁度系数λ的增大而减小；临界起动流速V起动随块体扁度系数λ的增大而增大。其临界止动流速V止动、临界起动流速V起动及稳定系数K值计算结果见表3。

2．2．2 扁钢筋笼

光滑水泥面上不同扁度系数的扁钢筋笼的止动和起动试验结果表明：扁钢筋笼的止动稳定系数K起动值范围为0．60～0．95，均值为0．77；其起动稳定系数K起动值范围为0．79～1．08，均值为0．90。稳定系数K止动及K起动均随扁度系数λ增大而增大，临界止动流速、临界起动流速V起动也均随扁度系数增大而增大。光滑水泥面上扁钢筋笼稳定系数K计算结果见表4。

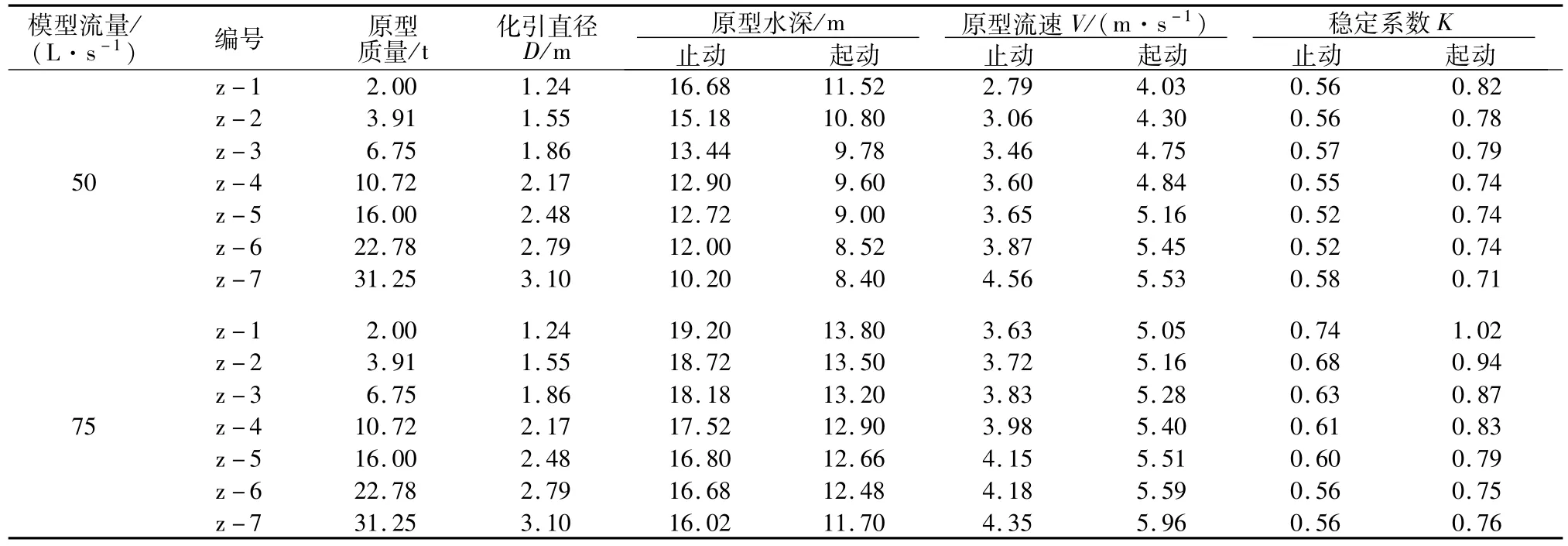
表1 光滑水泥面上正方体钢筋笼稳定系数计算结果Table 1 Computation result of the stability coefficient of cubic steel reinforcement cages on smooth cement surface

表2 Δ＝0．3 m石料垫底时正方体钢筋笼稳定系数计算结果Table 2 Computation result of the stability coefficient of cubic steel reinforcement cages on stone bed（Δ＝0．3m）

3 六面体钢筋笼稳定计算公式拟合与验证

3．1 六面体钢筋笼的稳定计算公式的拟合

3．1．1 正六面体钢筋笼的稳定计算公式

光滑水泥面上正方体钢筋的止动稳定系数K止动均值为0．59，其起动稳定系数均值K起动为0．81，代入伊兹巴斯公式得

式中：γs为钢筋笼的重度，g为重力加速度。

3．1．2 扁度系数λ的引入

在泥沙起动流速公式中，通常采用扁度系数λ的指数形式对卵石的起动流速进行修正，指数通常取1／3～1／2［2］，韩其为院士取0．45［3］。本文依据试验成果，将前述不同形状六面体钢筋笼稳定试验中得出的各工况正六面体的稳定系数均值作为拟合标准进行拟合。

（1）止动流速计算时，将各种扁度钢筋笼的止动稳定系数除以λ1／2，再进行平均，得出的稳定系数均值与正六面体止动稳定系数基本吻合，得到光滑面钢筋笼止动流速计算公式为

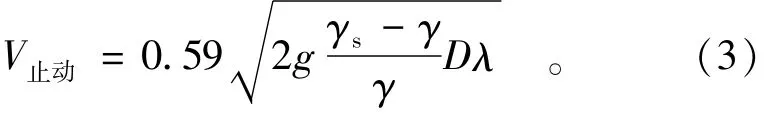
（2）起动流速计算时，将各种扁度钢筋笼的起动稳定系数除以λ1／3，再进行平均，得出的稳定系数均值与正六面体起动稳定系数基本吻合，得到光滑面钢筋笼起动流速计算公式为

3．1．3 相对糙率Δ／D的引入

在光滑水泥底板时，模型采用纯水泥收光表面，依据水力学教科书，其Δ＝0．000 25～0．001 25 mm，取均值0．000 75 mm，原型Δ＝0．045 m，16 t钢筋笼的化引直径D＝2．48 m，则Δ／D＝0．018。在Δ＝0．3 m石料垫底时，16 t钢筋笼的化引直径D＝2．48 m，则Δ／D＝0．121。

取正六面体钢筋笼的稳定系数均值为标准。光滑水泥底板时相应的止动稳定系数均值为0．58，起动稳定系数均值为0．77；Δ＝0．3 m石料垫底时相应的止动稳定系数均值为0．69，起动稳定系数均值为0．93。

表3 光滑水泥面上条形钢筋笼稳定系数K计算结果Table 3 Computation result of the stability coefficient K of steel reinforcement cages of bar shape on smooth cement surface

表4 光滑水泥面上扁钢筋笼稳定系数K计算结果Table 4 Computation result of stability coefficient K of flat steel reinforcement cages on smooth cement surface

式中：H为水深；A，B均为待定系数。考虑河床糙度影响，再依据试验数据对A，B值进行初步拟合。

止动计算时取A＝0．53，B＝0．47，得光滑水泥面时K＝0．59；Δ＝0．3 m垫底时，K＝0．69，与试验基本吻合。起动计算时取A＝0．65，B＝0．80，得光滑水泥面时K＝0．76；Δ＝0．3 m垫底时，K＝0．93，与试验吻合。

3．1．4 公式的完整形式

3．2 六面体钢筋笼的稳定计算公式的验证

利用式（6）及式（7），对Δ＝0．3m石料垫底情况下扁六面体钢筋笼的抗冲流速予以验证。止动及起动流速计算结果及实测数据见表5。依据式（6）及式（7）计算的流速V计算与扁度系数λ关系曲线及试验值与扁度系数λ关系曲线对比见图1。

图1 止动、起动流速计算值与试验值比较Fig．1 Comparison between computed values and measured values of the flow velocity for movement stopping and movement initiation

由表5和图1可知，拟合的公式计算值与试验值基本吻合，各种块体的起动流速与起动流速平均值与计算值的误差很小。

4 四面体钢筋笼的稳定性研究

四面体具有重心低、结构上易于稳定特点，将其形体特性与钢筋笼的透水性及可充分利用当地石材增大单体尺度等特性结合起来构成四面体钢筋笼，以期获得稳定性较好且经济实用的新型截流人工块体。

为方便比较，试验采取了分别与前述正方体钢筋笼z 3至z 7质量相同的6．75，10．72，16．00，22．78，31．25 t的5种四面体钢筋笼，整体重度均采用19．6 kN／m3。

4．1 光滑水泥面上

光滑水泥面上不同规格四面体钢筋笼的止动和起动试验结果表明：其止动稳定系数K止动值范围为0．68～0．75，均值为0．70（正六面体均值为0．57）；其起动稳定系数K起动值范围为0．70～0．79，均值为0．76（正六面体均值为0．77）。临界止动流速和临界起动流速均随块体质量的增加而增大，而止动稳定系数和起动稳定系数较为稳定，随块体质量的增大而减小的趋势不显著。光滑水泥面上四面体钢筋笼稳定系数计算结果见表6。

4．2 Δ＝0．3 m石料垫底

Δ＝0．3 m（原型）石料垫底条件下不同规格四面体钢筋笼的止动和起动试验结果表明：其止动稳定系数K止动值范围为0．82～0．90，均值为0．86（正六面体均值为0．69）；其起动稳定系数K起动值范围为1．01～1．15，均值为1．06（正六面体均值为0．95）；临界止动流速和临界起动流速均随块体质量的增加而增大，而止动稳定系数和起动稳定系数较为稳定，随块体质量的增大而减小的趋势不显著。Δ＝0．3 m石料垫底时四面体钢筋笼稳定系数计算结果见表7。

与前述相同质量的正方体钢筋笼对比可知，就截流抛投止动而言，四面体钢筋笼的稳定性明显高于正方体钢筋笼，而对于护底起动而言，两者的稳定性相差不大。

表5 扁钢筋笼抗冲流速计算值与试验值比较（Δ＝0．3 m石料垫底时）Table 5 Comparison between computed values and measured values of scour resistance velocity for flat steel reinforcement cages on stone bed（Δ＝0．3 m）

表6 光滑水泥面上四面体钢筋笼稳定系数计算结果Table 6 Computation result of stability coefficient of steel reinforcement cages w ith tetrahedral shape on smooth cement surface

表7 Δ＝0．3 m石料垫底时四面体钢筋笼稳定系数计算结果Table 7 Computation result of stability coefficient of steel reinforcement cages w ith tetrahedral shape on stone bed（Δ＝0．3 m）

5 结 论

（1）钢筋笼具有易于利用当地天然中小石料，透水性良好，制作加工简单，其抗冲能力明显高于现场一般石料的特点，在截流工程和护岸工程中均得到了广泛应用。鉴于以往成果未涉及钢筋笼的稳定性及计算方法，本文通过试验研究，结合笔者所在单位（长江科学院）提出的截流块体实用计算公式，分析了六面体钢筋笼的稳定特性，拟合了考虑质量、形状特性、床面相对糙度的六面体钢筋笼计算公式，经试验验证具有较好的计算精度，同时具有较大的实用价值和学术价值，可供设计及施工单位参考。

（2）本文提出的新型截流人工块体——四面体钢筋笼，具有重心低，结构上易于稳定，透水性强，可充分利用当地石材增大单体尺度等特性，经试验研究发现：四面体钢筋笼用于截流抛投这类止动问题的工程，其止动稳定性明显高于相同质量的正方体钢筋笼；而对于护底等起动问题的工程，两者起动稳定性相差不大。

［1］ ISBASH CB．河道截流水力学［M］．黄河三门峡工程局译．北京：中国工业出版社，1964．（ISBASH C B．River Closure Hydraulics［M］．Translated by Bureau of Sanmenxia Project of Yellow River．Beijing：China In dustry Press，1964．（in Chinese））

［2］ 宾景洁．川江卵石运动规律水槽试验报告［R］．武汉：长江水利水电科学院，武汉水利电力学院，1960．（BING Jing jie．Experimental Report on the Movement Rule of Pebble from Chuanjiang River in the Test Sink［J］．Wuhan：Yangtze River Water Resources and Hy dropower Scientific Research Institute and Wuhan Col lege of Hydraulic and Electric Engineering，1960．（in Chinese））

［3］ 韩其为，何明民．泥沙起动规律及起动流速［M］．北京：科学出版杜，1999．（HAN Qi wei，HE Ming min．Incipient Rule and Incipient Velocity of Sediment［M］．Beijing：Science Press，1999．（in Chinese））

［4］ 汪定扬．立堵截流实用水力学计算［J］．水利学报，1983，（9）：11－18．（WANG Ding yang．Practical Hy draulic Calculation in End dump River Closure［J］．Journal of Hydraulic Engineering，1983，（9）：11－18．（in Chinese） ）

（编辑：黄 玲）

Computational M ethod for the Stability of Steel Reinforcement Cage App lied in River Closure

LIXue hai1，CHENG Zi bing1，WANG Shi peng2，SHIJiao hao1
（1．Hydraulics Department，Yangtze River Scientific Research Institute，Wuhan 430010，China；2．Wuhan Changke Engineering Construction Supervision Co．Ltd．，Yangtze River Scientific Research Institute，Wuhan 430010，China）

The steel reinforcement cages with hexahedral shape are widely applied to river closure．Through tests and engineering example verifications focusing on weight，shape and bottom protection，the related formulas are fit ted for the first time to compute the flow velocities for movement stopping and movement initiation of hexahedral steel reinforcement cages in consideration of cage shape and bed roughness．The fitted formulas are of high accuracy and practicality．In addition，tests on the stability of steel reinforcement cage with tetrahedral shape revealed that itsmovement stopping stability is prior to that of hexahedral cages of the same weight in the case of end dump clo sure；whereas for bottom protection，the difference in movement initiation stability is little．

river closure；steel reinforcement cagewith hexahedral shape；steel reinforcement cagewith tetrahedral shape；stability behavior；influencing factor；computational formula

TV551

A

1001－5485（2013）08－0031－06

汪定扬［4］提出的块体稳定实用计算公式为

10．3969／j．issn．1001－5485．2013．08．008

2013，30（08）：31－36

2013－05－24

国家“十一五”科技支撑项目（2008BAB29B02）

李学海（1966－），男，湖南宁乡人，教授级高级工程师，博士，研究方向为水力学及流态力学，（电话）027－82823060（电子信箱）65689＠sina．com。