截流块体稳定影响因素及实用计算公式

黄国兵，李学海，程子兵，胡国毅

（长江科学院a．水力学研究所；b．研究生部，武汉 430010）

截流块体稳定影响因素及实用计算公式

黄国兵a，李学海a，程子兵a，胡国毅b

（长江科学院a．水力学研究所；b．研究生部，武汉 430010）

截流块体稳定计算是截流设计的重要基础。基于通过受力分析得出的基本表达式，结合试验和实践成果，剖析了影响截流块体稳定的主要因素，分析了截流块体稳定经典计算公式的适用条件。结果表明：在截流龙口水流垂线流速分布呈非矩形分布时，需综合考虑水深H、垂线流速系数α及相对糙度Δ／D、绕流系数ξ等影响因素；通过系列模型试验及工程实例验证，得出了考虑上述影响因素的平堵截流和立堵截流不同阶段、不同堤头形态的截流块体稳定实用计算表达式。对截流块体稳定理论及经典计算公式进行了补充和完善。

截流块体；稳定性；受力分析；影响因素；计算公式；途径

1 截流块体稳定影响因素分析

平底河床上的截流块体，其稳定计算式基于起动概念，通过块体受力分析，可得出基本表达式（1）［1］，即

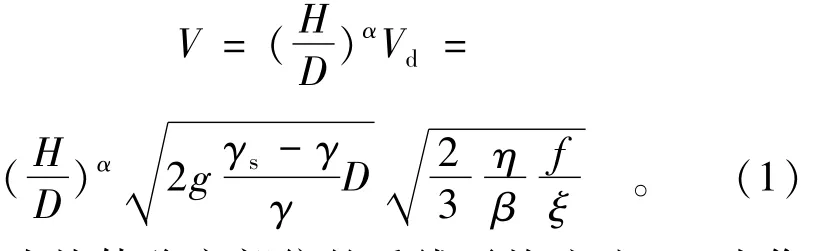
式中：V为块体稳定部位的垂线平均流速；Vd为作用于块体高度内的局部平均流速；D为块体化引成球体的粒径；H为块体稳定部位的水深；α为垂线流速分布系数；β为迎水面积修正系数；η为块体形状系数；f为含滑动摩擦系数或滚动摩擦系数；绕流系数ξ含正面推力系数ξx和上举力系数ξy；γs，γ分别为块体及水的重度；g为重力加速度。由式（1）可知，截流块体稳定的影响因素主要涉及龙口水流条件、抛投材料的物理力学特性、接触边界条件及其相互作用。

1．1 龙口水流条件

龙口水流条件包括截流龙口流速V、水深H、垂线流速分布系数α、绕流系数ξ等。龙口流速V是决定抛投材料是否稳定的动力源，其大小主要取决于龙口流量与龙口断面形态，龙口流量和龙口过水断面面积随口门束窄而减小，龙口流速在达到最大前随龙口束窄而增大；在达到最大后随龙口束窄而逐渐减小。水深H越大，H／D也越大，块体所能抵抗的水流垂线平均流速也越大。垂线流速分布系数α随截流方案、截流方式、进占阶段不同而不同；绕流系数ξ则与水力要素、抛石边界、块石特性等密切相关，特性复杂。

1．2 抛投材料的物理力学特性

抛投材料的物理力学特性，包括抛投材料的重度γs、粒径大小D、块体形状系数η、迎水面积修正系数β等参数；群体抛投时，还包括群体材料的组成、级配、密实程度等。γs越大，其稳定性越好；单体材料的粒径或群体材料的中值粒径d50越大，其稳定性越好；η对块体稳定性的作用机理复杂，与水流的绕流特性相关，重心越低，稳定性越好；透水性越好，稳定性越好。

1．3 抛投边界及抛投强度

抛投边界包括摩擦系数f、相对糙度Δ／D（Δ为床面凸起高度）、堤头坡度θ、抛投材料休止角 以及覆盖层特性等堤头及河床的几何边界及材料组成参数。Δ／D越小，f越小，抛投材料的稳定性越差。堤头坡面上块体稳定性还与θ及 有关，堤头坡面的形态与截流方案、进占方式及阶段、抛投材料类型、覆盖层特性等密切相关，随口门束窄与进占材料、龙口水流相互作用而不断演化。河床覆盖层特性包括覆盖层的组成、厚度、级配、粗化情况及板结特性等，以往研究表明，无覆盖层时的块体稳定性主要取决于自身的形状特点，而有覆盖层时的块体稳定性主要取决于覆盖层的稳定。此外，增大抛投强度，可有效抑制龙口抛投材料的流失。

综上所述，截流块体稳定问题是典型的水土两相问题，涉及因素繁多，关系十分复杂。如何在截流块体稳定计算中充分反映各控制性影响因素的作用和影响，科学表征其相互关系，一直是截流施工水力学需解决的关键问题。

2 经典截流块体稳定计算式

截流块体稳定计算分平底河床和堤头坡面上的块体稳定2种情况。平底河床上块体稳定计算最有代表性的是前苏联伊兹巴斯公式［1］和我国的肖焕雄截流抛石稳定理论［2］以及长江科学院汪定扬提出的截流块体稳定实用计算公式［3］；而坡面上的块体稳定计算最有代表性的是司特芬逊（D．Stephen son）坡面块体稳定公式［4］和钟登华、毛寨汉的抛投块石稳定率模型［5］。这里重点分析平底河床上块体稳定计算研究成果及存在的问题。

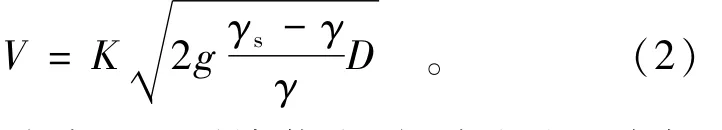
伊兹巴斯公式基于平堵截流、起动流速观点提出，滑动失稳取K1＝0．86；倾覆失稳取K2＝1．20；立堵时取K3＝0．90。肖焕雄基于立堵截流和止动流速观点，分单体、群体均匀料、群体混合料以及部分人工块体对K值进行了修正，单体石料K1取0．89，群体均匀料K2取1．07，群体混合料K3取0．93，砼立方体K4取0．76～0．80，砼四面体K5取0．68～0．72，使计算结果更接近于截流困难段的实际情况。但均未考虑水深因素、块体所处位置的垂线流速分布以及床面起伏不平引起的差异。

在实践中，依据式（2）得到的K值变化范围为0．4～2．7，变化范围较大，实际运用时难以把握。长江科学院汪定扬在葛洲坝大江截流设计研究期间发现相对糙度Δ／D值是影响K值的重要因素，基于日本学者岩恒雄一关于摩擦系数f的研究成果，即f是连续依赖于相对糙度Δ／D，其表达式f＝p＋q（Δ／ D）n，将式（1）中的通过试验提出了包含Δ／D的块体稳定实用计算公式，即

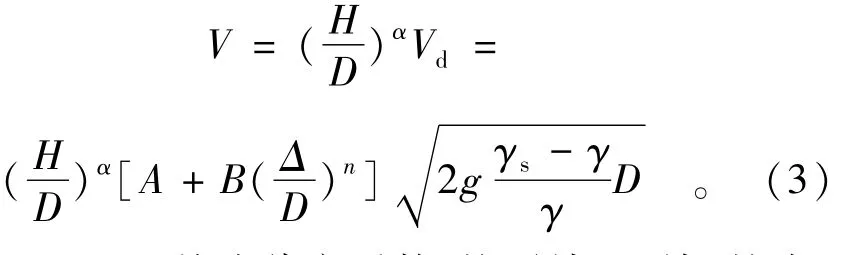
式中：A，B，n，α均为待定系数，按平堵、立堵、护岸、护底分情况通过试验得出后，便可用于各种条件下块体抗冲稳定计算。式中考虑了块体抛投稳定时的流速分布以及床面糙度的差异，较好地解释了平堵截流3个阶段的抛投块体运动、止动的物理意义，立堵截流连续抛投进占和换料时大块体的抗冲流速计算更符合实际。

之后长江科学院研究人员［6－7］结合国家“十一五”科技支撑项目（2008BAB29B02）对此进行了深入研究，进一步解析了式（3）中的A，B，n，α取值，并考虑了式（1）中的α，β，η以及ξ的影响。下面分平堵截流和立堵截流2种情况介绍相关研究成果。

3 平堵截流实用计算公式

3．1 正常河道分布下的实用计算公式

3．1．1 待定系数的选定

为确定A，B，n，α值，长江科学院在比尺为60的水槽模型中对不同重度（23．52～49 kN／m3）、不同质量及不同类型块体（3，5，8，15，25，62．5 t四面体和0．35～17．2 t的块石及异性体）、不同糙度基面上（Δ＝0，0．12，0．525，1．34 m），首先基于平堵截流、正常河道分布条件对块体稳定性进行了系列试验研究。

3．1．1．1 A值的选定

在光滑基面Δ＝0时，将式（3）和式（1）比较，可得

迎水面积修正系数β与块体形状有关，即与块体形状系数η关联，可令η＝β，则式（4）可变为

查询《水工设计手册》［8］和《流体力学》［9］教材，可知f＝0．15～0．2；绕流系数ξ＝0．6～1．1（立方体取1．1，四面体和块石在0．6～1．1间），则A＝根据试验实测底部流速，按计算A值，见表1，综合以上分析及表1计算结果，取A＝0．4。

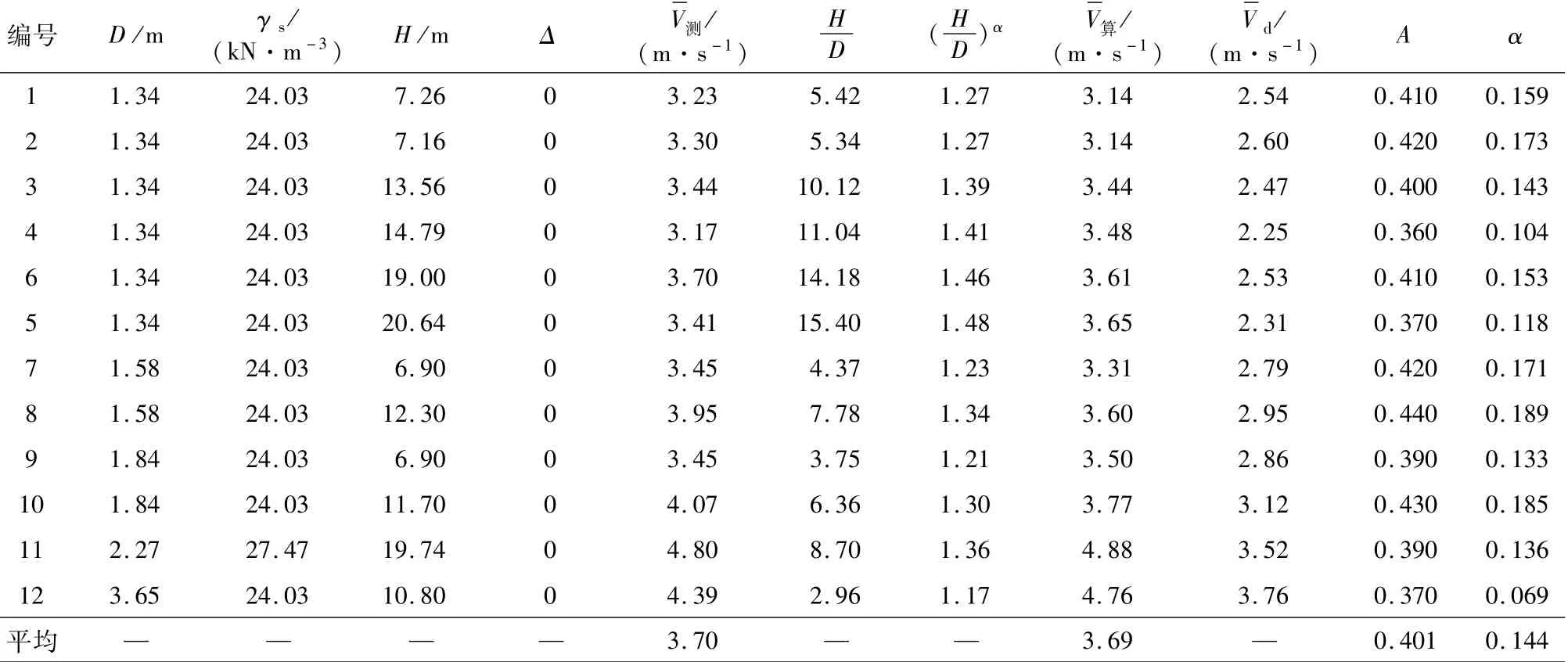
表1 依据实测资料的A值及α值计算Table 1 The com putation resu lts of A value andαvalue according to measured bottom velocity

3．1．1．2 α值的选定

在这里垂线流速分布取指数形式。在光滑基面Δ＝0时，α值计算式为

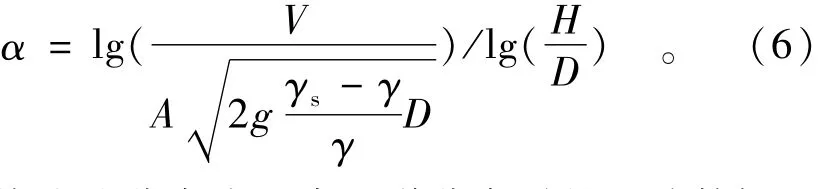
垂线流速分布为正常河道分布时的试验数据及α值计算见表1。表1中计算，α取不同值试算。取α＝1／7时计算得到的与实测值基本吻合；根据试验数据，按式（6）计算得到均值α为0．144≈1／7，故取α＝1／7。

3．1．1．3 β值的选定

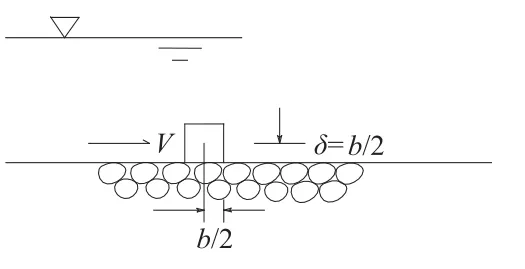
图1 粗糙面块体稳定状态示意图Fig．1 Sketch of stable status of rough blocks

根据试验观察，块石抛投到粗糙面上，当Δ／D≤1时，在块体处于临界平衡状态左右时，块石是先滚几下，能稳定下来的就不再滚了；否则便一直滚走。这样块体的平衡计算状态就如图1所示。

当Δ＝D时，即A＋B＝0．85～1．13；将A＝0．40代入得B＝0．45～0．73，平均值为0．59。依据实测资料计算的B值见表2。

表2 依据实测资料的B值计算Table 2 The com putation resu lt of B value according to measured data

根据上述分析及实测资料计算结果，取B＝0．59。

3．1．1．4 n值的选定

由于A，B，α已定，依据试验数据整理得n＝1／2。

3．1．2 正常河道分布下的实用计算公式

止动流速计算式为

根据试验，有V起动＝（1．1～1．2）V止动，进而得到起动流速计算式为

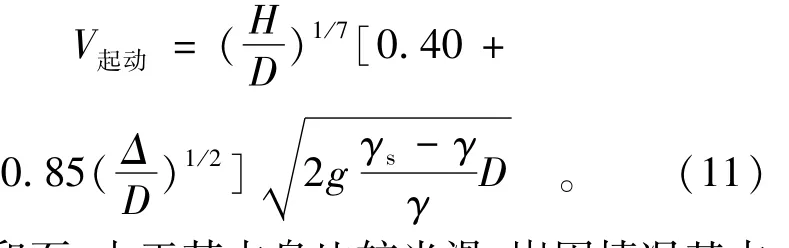
对于卵石，由于其本身比较光滑，嵌固情况基本相同，故起动流速总是等于止动流速。根据资料分析得

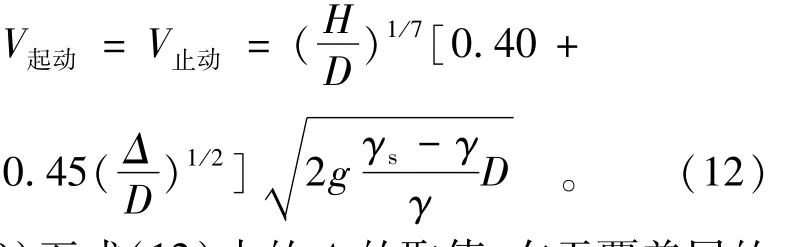
式（10）至式（12）中的Δ的取值，在无覆盖层的光滑河床，取Δ＝0；较糙的基岩取Δ＝δ；可令

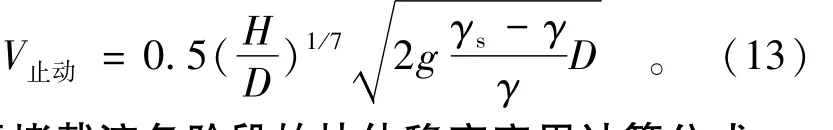
3．2 平堵截流各阶段的块体稳定实用计算公式

平堵截流分初抛、三角形断面以及扩展断面3个阶段。

3．2．1 初抛阶段

初抛块体时，此时河床表面覆盖层一般都已冲光，Δ＝0～δ（δ为某个较小的凸起高度值），代入式（10）得，得式（13）；垫底河床，可采用Δ＝d50。

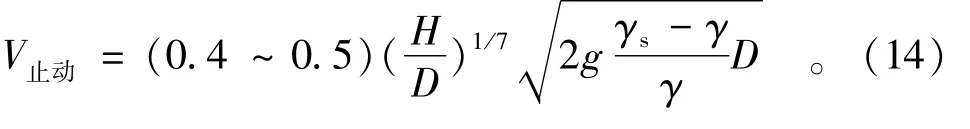
3．2．2 三角形断面阶段

三角形断面阶段的堆体顶部流速分布为表面小底部大，根据实测，此时Vd＝1．1V，即α值为负值，则

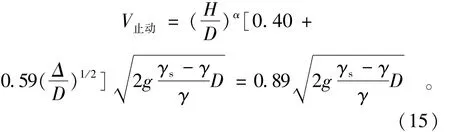
3．2．3 扩展断面阶段

在扩展断面阶段，Δ／D＝1，α可采用1／7，得

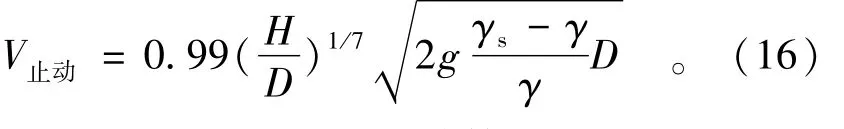
水深较大时，应按式（15）计算。

4 立堵截流实用计算公式

立堵截流情况下，要确定式（3）中的待定系数A，B，n，α值，需先分析立堵时块体稳定过程的特点和龙口各部位的流速分布特性，再通过试验及资料分析得出以上诸值。为此，对不可冲河床有护底和光滑基岩2种情况的立堵截流进行了试验研究。

4．1 块体稳定过程及龙口流速分布特性

4．1．1 块体稳定过程

立堵截流是龙口逐步束窄的过程，其稳定过程为：先抛小石，开始产生大量流失时，换较大料；换料后，常看到的是需有几个停下来，后续抛料才会逐渐停留下来，直到戗堤端形成冲刷面，此时达到该料的极限抗冲流速状态，称紧凑断面阶段；此后，截流戗堤断面虽延伸，块体不流走，称扩展断面阶段；之后，当龙口较宽时，龙口流速虽接近成舌流速，但两侧截流戗堤抛投滑落的石料不能在近处相撞，块体被冲向下游，会形成大量流失；当龙口较窄时（一般b／h下≤5．0），两侧截流戗堤抛投滑落的石料能在龙口相撞消能并停下形成舌根，后续抛石使舌根向上游延伸直至合龙，称成舌阶段。

4．1．2 龙口流速分布特性

立堵进占时龙口流速分布很复杂，有水流弗氏数、龙口束窄度、河床的糙率、戗堤形状及对称性等影响因素。龙口的最大流速一般在收缩断面处，其值一般略大于按戗堤上下游落差计算所得流速，窄龙口时，（Z为龙口上下游水位差），对于对称的双向立堵截流，截流戗堤从开始进占至合拢，龙口中心线上的垂线流速分布，轴线以上为上大下小，即V底＜V表，轴线附近V底≈V表，轴线以下则呈上小下大趋势，即V底＞V表。宽龙口时，龙口的垂线流速分布接近正常河道分布，α＝1／6～1／7；随龙口束窄，龙口轴线处的垂线流速分布逐渐由“半U”型的河道型分布转化为矩形分布，流速分布趋于均匀，龙口中心V底＝V表，靠近戗堤脚仍是V底＜V表，α＝1／10～1／12。过轴线以后底流速越来越小，窄龙口时在l＝2l0（l0为三角形戗堤纵向底宽）处α＝1／17，在l＝（2～3）l0处，α≈1／5～1／4，有时底部流速可为零，龙口护底末端底部流速为负。

4．2 立堵截流各阶段的块体稳定实用计算公式

分连续抛投进占和换料2种情况讨论。

4．2．1 连续抛投进占情况

4．2．1．1 紧凑断面

与平堵时块体为孤立情况不同，此时块体旁靠

戗堤脚，故A立≥A平。由在光滑基岩（Δ＝δ≠0）试验结果得A立＝0．65，则B立＝0．35。根据龙口流速分布试验得α＝1／10。最后得

4．2．1．3 成舌根

l≈（1．5～2．0）l0，此时A，B值与式（17）相同。由试验得α＝1／4～1／5，宽龙口时形成不了舌根不予考虑。窄龙口时，则：

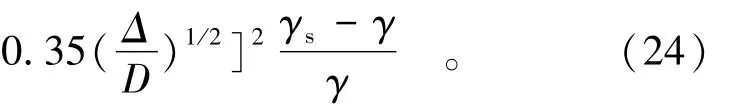
舌根形成后便渐渐形成舌头。块体的稳定条件改善了，此时就像平堵Δ＝D，同时舌体形成使其上流速分布改变，α≤1／7，故成舌后（窄龙口）实际抗冲能力为：

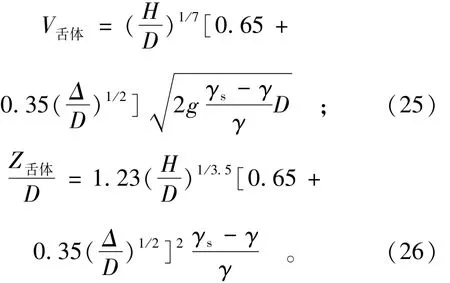
值得注意的是，在应用式（26）时，要使b／h下≤5．0，否则将有块体大量流失。

4．2．2 换料抛投进占情况

不同进占方式的块体稳定边界见图2。

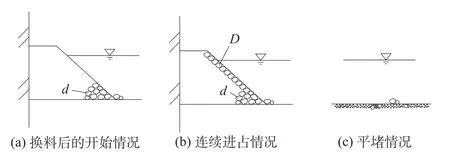
图2 不同进占方式的块体稳定边界Fig．2 Stability boundary of different embankment building methods

图2 中，d为先期抛投已稳定的材料粒径，D为抛投块体引化为球体的粒径。图2（a），2（b）比较可以看到，换料时块体稳定条件与连续进占时是不同的。连续进占时d＝D；而换料时d≠D。因A＝f（d／D），A值应随d／D变化。但为了计算简便，根据试验资料分析，取A＝0．55即能满足要求。于是得：

紧凑断面时

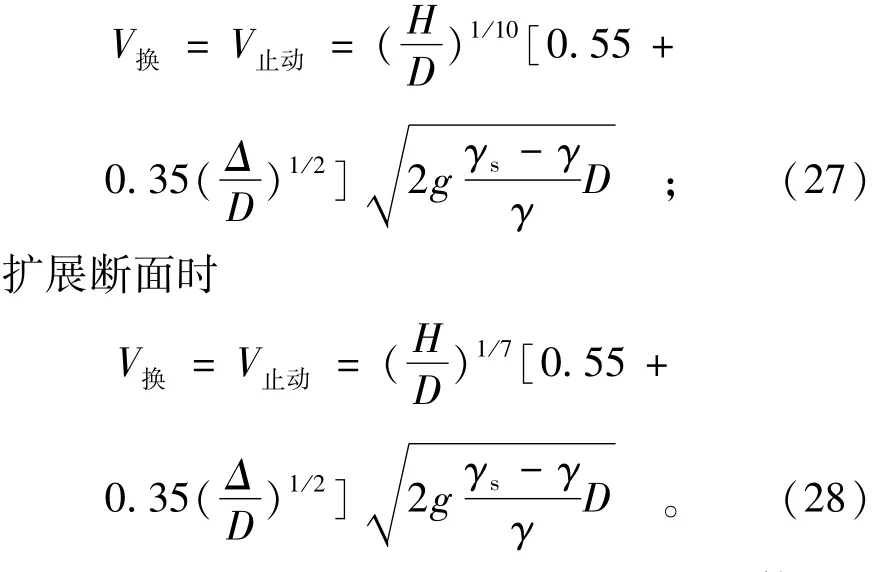
式（27）和式（28）适用于只抛少量大块体（如10～20个）时采用。

5 截流块体实用计算公式汇总

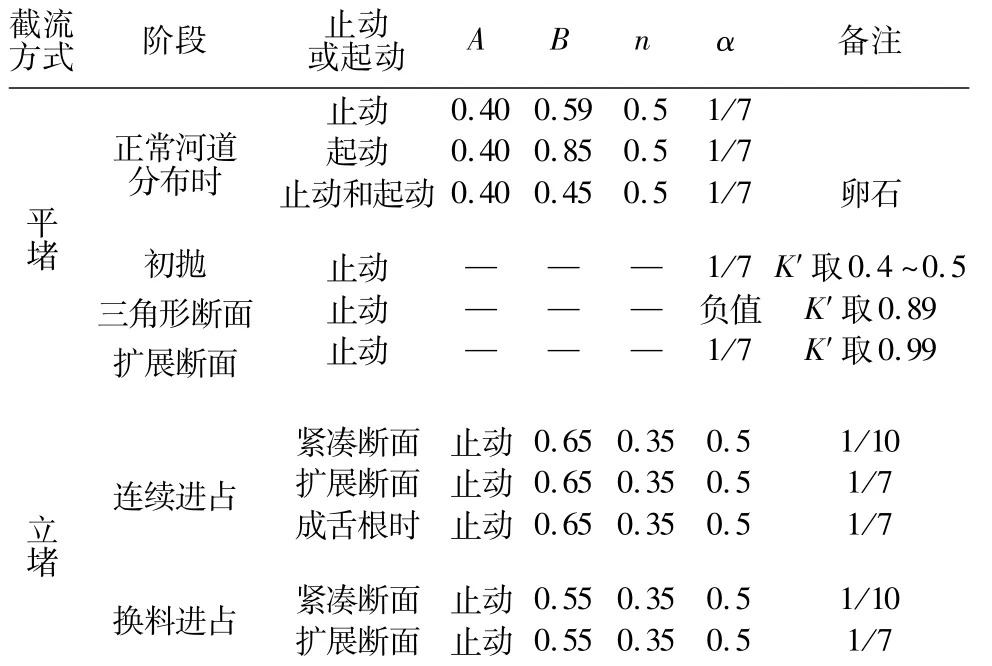
表3 平堵、立堵截流不同阶段、不同堤头形态下的A，B，n，α取值Table 3 Values of A，B，n，αfor different construction periods and different embankment head shapes in full w idth rising closure and end dump closure

6 结 论

（1）截流块体稳定的影响因素主要涉及龙口水流条件、抛投材料的物理力学特性、接触边界条件及其相互作用等。包括龙口流速V、龙口水深H、垂线流速分布特性系数α、绕流性系数ξ等龙口水力特性参数；重度γs、粒径大小D、块体形状系数η、迎水面积修正系数β、绕流系数ξ等抛投材料的物理力学性质参数；摩擦系数f、糙度Δ、相对糙度Δ／D、坡度θ、材料的休止角 以及覆盖层特性参数等堤头及河床的几何边界及材料组成参数。

（2）长江科学院提出的块体稳定实用计算公式，分平堵截流和立堵截流，对不同阶段、不同堤头形态的A，B，n，α取值进行了进一步解析，块体稳定实用计算公式将垂线流速分布系数α、迎水面积修正系数β、块体形状系数η以及绕流系数ξ的影响纳入了A，B，n，α中，较好地解释平堵截流3个阶段的抛投块体运动、止动的物理意义，使立堵截流连续抛投进占和换料抛投进占的块体稳定计算结果与实际情况更为接近。

［1］ 伊兹巴斯C．B．河道截流水力学［M］．北京：中国工业出版社，1964．（ISBASH C B．River Closure Hydraulics［M］．Beijing：China Industry Press，1964．（in Chi nese））

［2］ 肖焕雄．立堵截流抛石粒径计算研究［J］．水电站设计，2003，（3）：1－7．（XIAO Huan xiong．Estimation Re search on Riprap Grain Size for Closure by Vertical Blockade［J］．Design of Hydroelectric Power Station，2003，（3）：1－7．（in Chinese））

［3］ 汪定扬．立堵截流实用水力学计算［J］．水利学报，1983，（9）：11－18．（WANG Ding yang．Practical Hy draulic Calculation in End Dump River Closure［J］．Journal of Hydraulic Engineering，1983，（9）：11－18．（in Chinese））

［4］ 肖焕雄．施工水力学［M］．北京：水利电力出版社，1992．（XIAO Huan xiong．Construction Hydraulics［M］．Beijing：Water Resources and Electric Power Press，1992．（in Chinese））

［5］ 钟登华，毛寨汉．床面起伏影响下截流抛石稳定研究［J］．水力发电学报，2003，（1）：83－88．（ZHONG Deng hua，MAO Zhai han．Research on Stability of Rip rap Influenced by Boundary of Riverbed During River Closure［J］．Journal of Hydroelectric Engineering，2003，（1）：83－88．（in Chinese））

［6］ 郭熙灵，黄国兵，李学海．深厚覆盖层条件下施工导截流关键技术问题研究［J］．长江科学院院报，2011，28（6）：10－15．（GUO Xi ling，HUANG Guo bing，LI Xue hai．Critical Technical Issues of Diversion and River Closure Construction Under Deep Thickness Covering Layer Condition［J］．Journal of Yangtze River Scientific Research Institute，2011，28（6）：10－15．（in Chi nese））

［7］ 李学海，韩继斌，程子兵．减轻立堵截流难度措施研究进展［J］．长江科学院院报，2010，27（8）：29－33．（LI Xue hai，HAN Ji bin，CHENG Zi bing．Research Progress in Technology of Reducing Difficulty of Vertical Closure［J］．Journal of Yangtze River Scientific Research Institute，2010，27（8）：29－33．（in Chinese））

［8］ 左东启，顾兆勋，王文修．水工设计手册第一卷［M］．北京：水利电力出版社，1983．（ZUO Dong qi，GU Zhao xun，WANGWen xiu．Manual of Hydraulic Engineering Design（1st Volume）［M］．Beijing：Water Resources and Electric Power Press，1983．（in Chinese））

［9］ 吴望一．流体力学［M］．北京：北京大学出版社，1982．（WUWang yi．Fluid Mechanics［M］．Beijing：Peking University Press，1982．（in Chinese） ）

（编辑：周晓雁 姜小兰）

Stability Analysis of Block for River Closure and Practical Formula

HUANG Guo bing1，LIXue hai1，CHENG Zi bing1，HU Guo yi2
（1．Hydraulics Department，Yangtze River Scientific Research Institute，Wuhan 430010，China；2．Graduate Department，Yangtze River Scientific Research Institute，Wuhan 430010，China；）

The stability calculation of river closure block is an important basis of river closure design．According to basic formulas obtained from force analysis and experimental research data，the influencing factors of block stability and the applicable conditions of classic formulas for block stability are analyzed．It is pointed out that these parame ters aswater depth H，vertical velocity coefficientα，relative roughnessΔ／D and circumferentialmotion coefficient ξshould be considered when vertical velocity distribution is not rectangular in the closure gap．Through model tests and project example verification，the practical computing formulas of block stability are put forward for full width rising and end dump closuremethods in different constructing periods and with different embankment head shapes．The research result is a supplement and improvement to the stability theory of river closure block．

block for river closure；stability；force analysis；influencing factor；computational formula；measures

TV551．2

A

1001－5485（2013）08－0025－06

10．3969／j．issn．1001－5485．2013．08．007

2013，30（08）：25－30，36

2013－05－06；

2013－07－03

国家“十一五”科技支撑项目（2008BAB29B02）

黄国兵（1963－），男，湖北天门人，教授级高级工程师，研究方向为水力学及流态力学，（电话）027－82926893（电子信箱）huanggb＠mail．crsri．cn。

李学海（1966－），男，湖南宁乡人，教授级高级工程师，博士，研究方向为水力学及流态力学，（电话）027－82823060（电子信箱）65689＠sina．com。