时间域航空电磁系统瞬变全时响应正演模拟
殷长春,黄 威,贲 放
吉林大学地球探测科学与技术学院,长春 130026
1 引 言
航空电磁法(Airborne Electromagnetics,简称AEM),是用来快速地质填图、普查良导电金属矿、地下水及环境和工程监测等领域的航空物探方法[1].该方法优势在于速度快、成本低、通行性好,尤其是在地形地质条件复杂地区,比如沙漠地区、山区、森林、沼泽,以及大量植被覆盖地区,可以达到一般物探所不能达到的效果[2].航空电磁法根据发射波形的不同分为时间域和频率域系统.
时间域直升机吊舱系统是以直升机为载体,在飞行过程中通过安装在吊舱上的发射线圈,向地下发送一次脉冲磁场,即为一次场;在其激发下,地下的地质体中激发出感应涡流,将产生随时间变化的感应二次场.通过采集地下返回的电磁信号,可达到探测地下地质体的目的[3].该方法由于直升机飞行速度慢,数据采样密集,具有很高的横向分辨率,可以较好地探测地下地质构造.由于时间域系统进行纯异常观测,且发射功率很大,可探测较大深度的勘探目标.
国外的航空系统目前已较发达,加拿大Fugro航空地球物理公司的HeliGEOTEM系统,Geotech公司的VTEM系统,Aeroquest公司的AeroTEM系统,丹麦Aarhus大学的SkyTEM系统等已广泛应用于地质填图、地下水和矿产资源调查[4].有关航空电磁系统响应的理论和应用研究国外也起步较早.上世纪50年代释[7];1998年,Morrison等将早年有关地面瞬变电磁法的研究成果应用到航空电磁存在局部不均匀体的异常响应特征研究[8];同年,Barongo通过将频率域的计算结果转换到时间域研究了航空瞬变电磁法的一维正演问题[9];2003年,Balch和Rudd等对三角波激励下AeroTEM系统的on-time数据进行反演解释[10];2008年,Yin等对半正弦和梯形波激励均匀半空模型的on-time和off-time电磁响应特征进行模拟和分析[11].
我国航空电磁勘探开发研究始于20世纪70年代.1979年航空物探总队从国外引进双水獭翼尖硬架三频电磁系统,目前已退役.后来,国内自行研制的Y-11飞机翼尖硬架双频航电系统.2006年,吉林大学开始自主研制时间域直升机吊舱系统,项目组研制出JLATEM吊舱式时间域直升机电磁勘查系统样机,目前仍处于试验阶段.国内引进的系统目前仅有国土资源部航遥中心从加拿大Aeroquest公司引进的AeroTEM-III型时间域航空电磁系统.国内很多学者很早就开始研究航空电磁法,1980年朴化荣等发表了均匀大地上空的时间域电磁响应,并解释了不同飞行高度观测的时间域航空电磁资料[12];随后,更多学者投入到航空电磁研究领域.2003年罗延钟等基于电磁勘探理论推导出层状大地时间域航空电磁法偶极-偶极装置的正演计算公式和算法[13];2005年阮百尧等对均匀水平大地上频率域垂直磁偶源电磁场数字滤波解法进行研究[14];2010年吴小平等利用δ单脉冲函数作为激励源的时间域电磁响应以实现电磁测深[15];2011年王世隆等对同心补偿式直升机时间域航空电磁法吊舱校准装置进行了研究[16].
本文推广了Yin[11]等人的算法理论,不再仅仅计算均匀半空间电磁响应而是计算任意层状介质的电磁响应,并将数值转换方法推广到三维电磁响应的正演模拟.我们首先利用快速汉克尔变换数值滤波算法计算频率域电磁响应,再通过傅里叶变换将频率域电磁响应转换到时间域,得到航空电磁系统的阶跃响应.最后,通过和实际发射波形的褶积获得对于任意发射波形的正演模拟算法.我们以目前世界上最先进的航空电磁直升机吊舱系统HeliGEOTEM为例来说明算法的有效性.
2 航空直升机吊舱系统的正演理论
2.1 垂直磁偶极子的电磁响应公式
在目前航空电磁系统中,垂直磁偶极子是最常用的发射源装置.在这种装置下可以测量各磁场分量.这里主要研究同线x方向和垂直z方向上的磁场分量的正演计算.我们假设直角坐标系的原点位于垂直磁偶极正下方的地表,z坐标向下为正,磁偶极子发射源的高度为h.参考图1,在测点(x,0,z)处沿着x方向的磁场水平分量为[17]
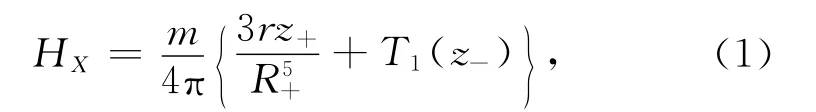
而磁场垂直分量HZ为

其中z±=h±z,R+=,m=nIS是发射偶极矩,而I,n,S分别表示发射电流、发射线圈匝数和面积;T(z-)是汉克尔积分,即
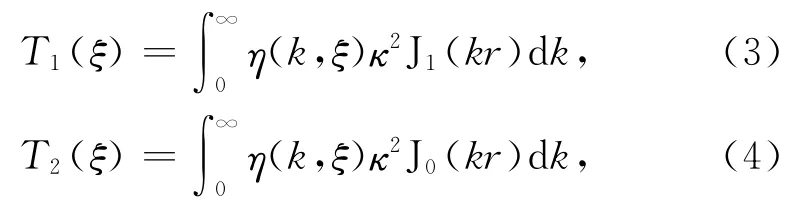
上式的积分称为汉克尔积分,J0(kr)和J1(kr)分别为零阶和一阶贝塞尔函数,核函数η(k,ξ)的循环算法参见 Yin和 Hodges[17].本文应用了 Yin和 Hodges[17]给出的100点汉克尔数值滤波系数计算 (3)~(4)式中的汉克尔积分.
2.2 频率域与时间域的转换关系
如果频率域中场值已知,就可通过傅里叶变换将频率域航空电磁响应转换到时间域

其中,B(ω)和BI(t)分别为航空电磁系统的频率域响应和对应的脉冲响应.本节为简化起见,我们省略场表达式中的空间坐标.当发射电流采用负阶跃电流i(t)=u(t)时,系统观测到的响应称为阶跃响应.由于阶跃函数的傅里叶变换为-1/iω,我们可得到频率域中谐变电磁场分量B(ω)和时间域中负阶跃电流激励下瞬变电磁响应BS(t)的对应关系[18]为
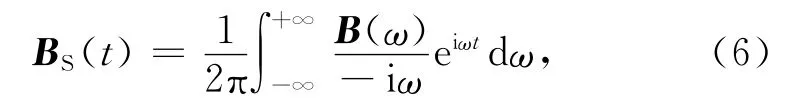
上式经过简单变换变成
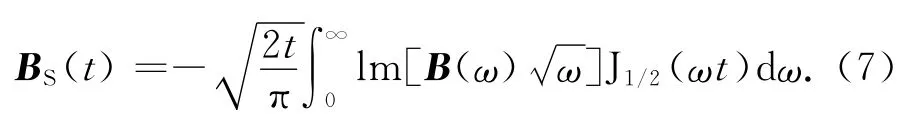
我们利用Yin等[11]给出的160点汉克尔滤波系数计算(7)式中的半整数阶汉克尔积分.
2.3 时间域航空电磁响应
时间域航空电磁响应传统的算法基于傅里叶变换,因此有关系式[19]

上式中B0(ω)是系统的单位脉冲响应,而I(ω)为发射电流的傅氏谱.利用卷积定理以及阶跃响应和脉冲响应之间的关系,得到任意发射电流时间域电磁响应的褶积公式:
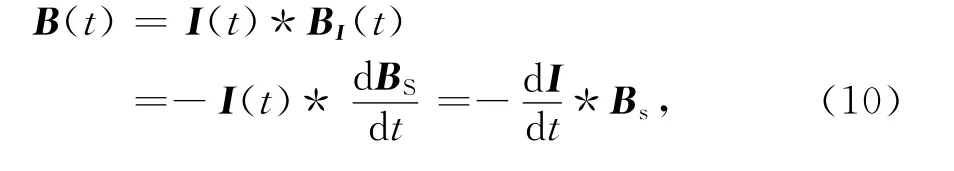
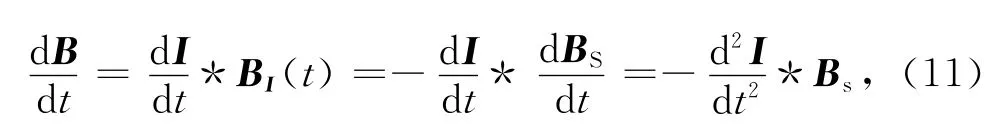
其中,I(t)是发射电流,而BI(t)和BS(t)分别是航空电磁系统的脉冲响应和阶跃响应.这里值得注意的是任何系统阶跃响应和脉冲响应均存在积分/微分的关系.方程(10)和(11)将 Yin等[17]给出的计算公式做了进一步延伸.
公式(10)和(11)中的褶积可以通过高斯积分来实现[20].因此,可得到

其中xi和wi分别为高斯抽样点坐标及对应的加权系数.
3 一维层状介质脉冲响应和阶跃响应特征分析
3.1 模型参数介绍
假设垂直磁偶极发射源位于直角坐标系原点的正上方(取Z坐标垂直向下,如图1),测点坐标为(x,0,z).h=30m 为发射线圈离地面的高度,z=50m为接收线圈离地面的高度,r=10m为发射线圈和接收线圈之间的水平距离.航空电磁系统的发射偶极矩为615000Am2.图1给出电磁系统模型示意图.我们分别讨论表1中均匀半空间、两层和三层介质的情况.

表1 模型参数Table 1 Model parameters
3.2 脉冲函数和阶跃函数的电磁响应
图2给出航空电磁系统的脉冲响应和阶跃响应.由图可以看出,无论是同线分量还是垂直分量,航空电磁系统的脉冲响应在时间接近0时出现奇异性[图2a,b],而阶跃响应(脉冲响应的积分)则保持平稳状态并随时间减小趋近于零[图2c,d].因此,利用系统脉冲响应的褶积运算不稳定,而利用系统阶跃响应的褶积运算是稳定的.这更说明,尽管在公式(10)、(11)中的褶积在数学上是等价的,但由于脉冲响应在t=0时刻出现奇异性,公式(10)、(11)中只有最后的褶积方法是稳定可行的.鉴于此,本文利用(10)和(11)中的最后两式计算任意发射波形的航空电磁全时响应.
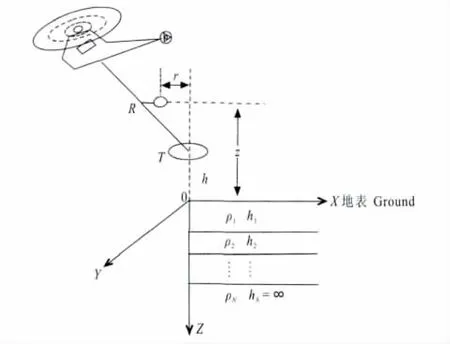
图1 模型示意图Fig.1 Sketch map of AEM system and the layered earth model
4 一维层状介质任意发射波形的电磁响应
4.1 发射波形参数和精度检验
下面以半正弦波为例讨论时间域航空电磁系统全时响应的正演模拟问题,参考Fugro的HeliGEOTEM系统.如图3,假设半正弦波的基频为f=30Hz,脉冲宽度为4ms,发射偶极矩为615000Am2.发射和接收机几何参数与图2所述相同.由于目前尚未见到国内外有关时间域航空电磁系统全时响应计算结果,我们针对Yin等[11]给出的半空间模型,利用本文提出的层状模型计算结果与其进行比较.如图4所示,吻合程度令人满意.

图2 层状介质的脉冲响应和阶跃响应(a)和(b)是x和z方向磁场的脉冲响应,而(c)和(d)是x和z方向磁场的阶跃响应.Fig.2 Impulse and step responses of AEM system for a layered medium,where(a)and(b)display the impulse system responses,while(c)and(d)display the step response.

图3 航空电磁半正弦发射波形Fig.3 Airborne EM half-sine transmitting waveform
4.2 一维层状介质的电磁响应
图5和6分别给出航空电磁系统全时响应B和dB/dt(地电模型参数见表1).为比较起见,同时给出利用系统阶跃响应和脉冲响应进行褶积的计算结果.
从图可以看出,无论是同线还是垂直分量,利用系统阶跃响应和发射电流褶积计算的磁场B和磁感应dB/dt之间保持很好的积分/导数关系,而利用脉冲响应计算的B和dB/dt不存在该积分/导数关系.另外,由脉冲响应计算的电磁响应与电阻率基本无关,响应曲线基本重合,不能反映地下电性分布特征.这说明算法存在问题.相反,由阶跃响应计算的电磁场响应很好地反映地下电性特征的变化.从图中可以比较明显地看出不同大地导电率对应不同的晚期衰减速率.大地越良导,电磁信号衰减越慢,反之大地越高阻,电磁信号衰减越快.
比较图5a和图5c、图6a和图6c可以看出,所有模型中B和dB/dt电磁响应x方向的幅值比z方向的幅值均小一个数量级,说明z方向的电磁响应具有较高垂向分辨率和勘探深度.进一步比较图5a和图5c可以看出,地下电性越良导,供电和断电(全时域)电磁响应信号B越强,供、断电期间的峰峰值越大且衰减越慢.因而时间域航空电磁系统可有效应用于地下良导体目标的勘探.比较图6a和图6c可以看出,地下电性越良导,电磁响应信号dB/dt越强,供、断电期间的峰峰值越大且衰减越慢.然而,和磁场响应B相比,磁感应dB/dt曲线形态更复杂,异常分辨能力明显减弱.

图4 本文计算结果和Yin[11]等的计算结果比较Fig.4 Modeling results of this paper compared with those from Yin et al.[11]

图5 航空电磁层状介质全时域电磁响应B计算结果其中(a)和(c)是利用系统阶跃响应进行褶积,而(b)和(d)是利用系统脉冲响应进行褶积.Fig.5 AEM full-time Bresponses over a layered medium for a half-sine transmitting wave,where (a)and (c)are magnetic field responses calculated by convolving the transmitting current with step response,while (b)and (d)are calculated by convolving with impulse response.
5 三维地质体的电磁响应
下面讨论利用积分方程方法计算三维不均匀体的时间域航空电磁响应.本文采用的频率域正演模拟是基于Raiche[21]提出的算法.它是利用并矢格林函数理论建立二次感应场和一次场的关系,求解异常体内感应电流分布,并通过对异常体内感应电流的体积分计算航空电磁系统的频率响应.通过汉克尔变换,将系统的频率响应转换到时间域,并通过和发射电流波形或其导数的褶积计算出航空电磁系统的全时域瞬变电磁响应.
5.1 三维模型及参数介绍
假设垂直磁偶极发射源位于三维异常体的正上方.航空电磁系统参数见图1,地下三维目标体的埋深为d,目标体的围岩电阻率为100Ωm.我们分别计算了两种情况:同一深度不同目标体电阻率ρ=1、10、100Ωm,及同一电阻率不同目标体深度d=10、30、50m.假设异常体的体积为50m×50m×200m,正演模拟时将其剖分为5m×5m×20m的单元.
5.2 三维地质体的电磁响应
图8给出三维地质体在同一电阻率ρ=1Ωm不同深度的电磁响应,而图9是三维地质体位于同一深度d=30m,其电阻率不同时的电磁响应.我们利用系统的阶跃响应与发射波形进行褶积计算出x和z方向磁场B和磁感应dB/dt响应.从图8a、8b和图9a、9b可以看出早期异常较大,说明供电期间的航空电磁信号易于分辨地下良导体;比较两图可以看出z方向幅值比x方向幅值至少高出一个数量级,这与一维层状介质的情况类似.比较图8c、8d可以看出不同埋深良导体无论在磁感应dB/dt还是在磁场响应B上均得到很好地反映.无论对于同线分量还是垂直分量,B和dB/dt之间均有很好的积分/导数一致性关系.
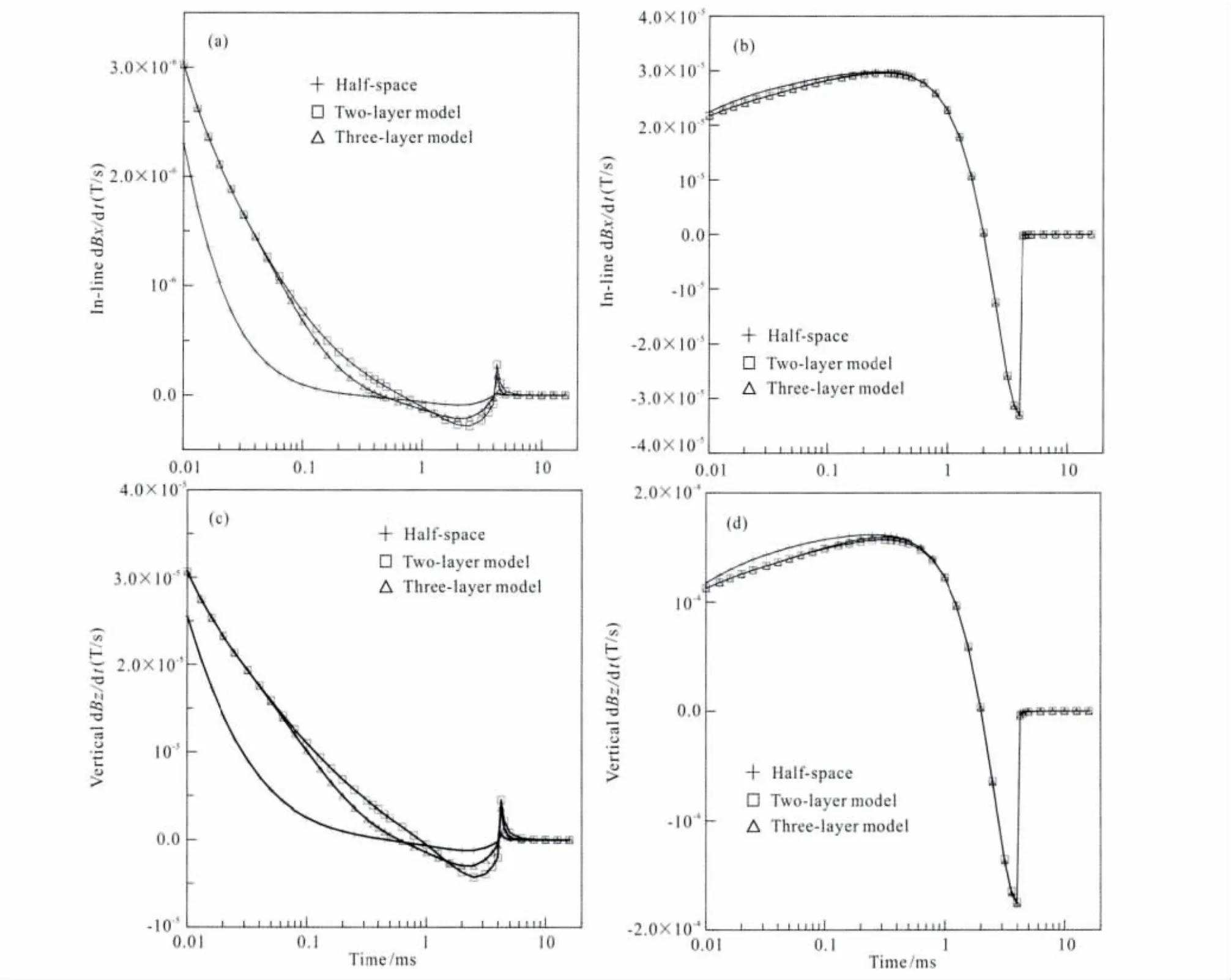
图6 航空电磁层状介质全时域电磁响应dB/dt计算结果(a)和(c)是利用系统阶跃响应进行褶积,而(b)和(d)是利用系统脉冲响应进行褶积.Fig.6 AEM full-time dB/dt responses over a layered medium for a half-sine transmitting wave,where(a)and (c)are dB/dt calculated by convolving the transmitting current with step response,while(b)and(d)are calculated by convolving with impulse response.
6 结 论
本文研究了时间域航空电磁系统瞬变全时域电磁响应的正演模拟问题,对于系统供、断电时产生的B和dB/dt的电磁响应给出了一个稳定的算法.较之于传统的算法,本方法计算更精确、稳定,并很好地保持了磁场B和磁感应dB/dt的一致性关系.文中给出的算法不仅适用于一维地质体,也适用于三维复杂地质模型电磁响应的正演模拟.
从理论模拟结果可见,航空瞬变电磁响应的垂直分量比同线分量信号强的多,因而具有较大勘探深度和较高分辨率.三维异常体的供电(on-time)电磁响应强,并且对异常体的导电性非常敏感,因此全时域航空电磁响应观测和解释易于识别地下良导体.
必须指出的是:本文提出的算法是利用系统阶跃响应和发射电流的导数进行褶积计算航空电磁响应,非常适合理论模型的正反演计算;对于实际发射波形,首先需要对其进行拟合,从而得到其导数才可计算出航空电磁响应.
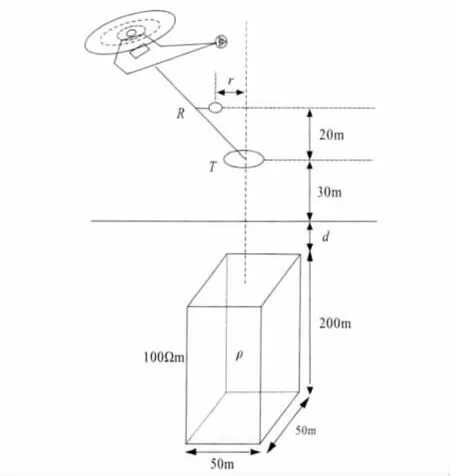
图7 三维地质体模型Fig.7 Three-dimensional geological model
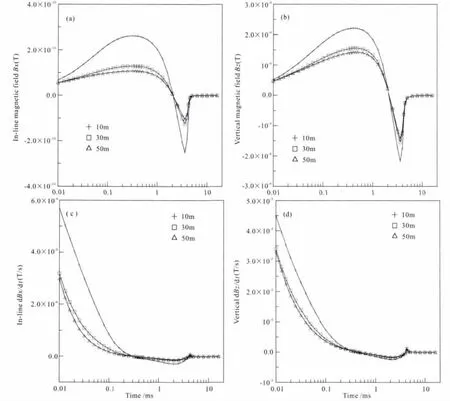
图8 同一电阻率不同深度三维地质体的航空电磁响应Fig.8 AEM responses for a three-dimensional geological body with the same resistivity but different depths
现在探讨一种新的思路:通过利用航空电磁系统接收机在飞行到很高高度时获得的参考信号来代替发射电流波形,并和系统阶跃响应进行褶积来计算航空电磁系统全时域电磁响应.这将是未来的研究方向.
(References)
[1]强建科,罗延钟,汤井田等.航空瞬变电磁法的全时域视电阻率计算方法.地球物理学进展,2010,25(5):1657-1661.Qiang J K,Luo Y Z,Tang J T,et al.The algorithm of alltime calculation of apparent resistivity for Airborne Transient Electromagnetic(ATEM)survey.Progress in Geophysics(in Chinese),2010,25(5):1657-1661.

图9 三维地质体在同一深度但具有不同电阻率的航空电磁响应Fig.9 AEM responses for a three-dimensional geological body with the same depth but different resistivities
[2]雷栋,胡祥云,张素芳.航空电磁法的发展现状.地质找矿论丛,2006,21(1):40-53.Lei D,Hu X Y,Zhang S F.Development status quo of airborne electromagnetic.Contributions to Geology and Mineral Resources Research (in Chinese),2006,21(1):40-53.
[3]牛之琏.时间域电磁法原理.长沙:中南大学出版社,2007.Niu Z L.Principle of Time-domain Electromagnetic Method(in Chinese).Changsha:Central South University Publishing House,2007.
[4]Smith R.Airborne electromagnetic methods:applications to minerals,water and hydrocarbon exploration.CSEG Distinguished Lecture Tour,2010.
[5]Dobrin M B.Introduction to Geophysical Prospecting.3rd ed.New York:McGraw-Hill,1976.
[6]Nerson P H and Morris D B.Theoretical response of a timedomain airborne,electromagnetic system.Geophysics,1969,34(5),729-738.
[7]Annan A P,Smith R S,Lemieux J,et al.Resistive-limit time-domain AEM apparent conductivity.Geophysics,1996,61(1):93-99.
[8]Morrison H F,Becker A,Hoversten G M.Physics of airborne EM systems.Exploration Geophysics,1998,29(2):97-102.
[9]Barongo J O.Selection of an appropriate model for the interpretation of time-domain airborne electromagnetic data for geological mapping.Exploration Geophysics,1998,29(2):107-110.
[10]Balch S J,Boyko W P,Paterson N R.The AeroTEM airborne electromagnetic system.The leading Edge,2003,22(6):562-566.
[11]Yin C,Smith R S,Hodges G,Anne P.Modeling results of on-and off-time B and dB/dt for time-domain airborne EM systems.Extended Abstract,70th Annual EAGE Conference and Exhibition,Rome,2008,1-4.
[12]朴化荣,沙树琴,王延良.均匀大地上空的时间域电磁响应.地球物理学报,1980,23(2):207-218.Piao H R, Sha S Q, Wang Y L. Time domain electromagnetic response above the surface of a homogeneous earth.Chinese J.Geophys.(in Chinese),1980,23(2):207-218.
[13]罗延钟,张胜业,王卫平.时间域航空电磁法-维正演研究.地球物理学报,2003,46(5):719-724.Luo Y Z,Zhang S Y,Wang W P.A research on one-dimension forward for aerial electromagnetic method in time domain.Chinese J.Geophys.(in Chinese),2003,46(5):719-724.
[14]阮百尧.均匀水平大地上频率域垂直磁偶源电磁场数值滤波解法.桂林工学院学报,2005,25(1):14-18.Run B Y.Digital filter method of evaluating electromagnetic field from a vertical magnetic dipole above the homogeneous earth.Journal of Guilin University of Technology (in Chinese),2005,25(1):14-18.
[15]吴小平,柳建新.一种广义时间域电磁测深法——单脉冲电磁测深方法.地球物理学进展,2010,25(6):2137-2143.Wu X P,Liu J X.A generalized time-domain electromagnetic sounding——theδfunction electromagnetic sounding.Progress in Geophysics(in Chinese),2010,25(6):2137-2143.
[16]王世隆,王言章,随阳轶等.同心补偿式直升机时间域航空电磁法吊舱校准装置研究.地球物理学报,2011,54(9):2397-2406.Wang S R,Wang Y Z,Sui Y Y,et al.A bird calibration device of helicopter-borne TEM with concentric bucking loop.Chinese J.Geophys.(in Chinese),2011,54(9):2397-2406.
[17]Yin C,Hodges G.Simulated annealing for airborne EM inversion.Geophysics,2007,72(4):F189-F196.
[18]Yin C.Electromagnetic induction in a layered conductor with arbitrary anisotropy [Ph.D.Thesis]Germany:Technical University of Braunschweig,1999.
[19]朴华荣.电磁测深法原理.北京:地质出版社,1990.Piao H R.The theory of Electromagnetic Sounding (in Chinese).Beijing:Geological Publishing House,1990.
[20]何光渝,周宇斌,张国凤.FORTRAN 77算法手册.北京:科学出版社,1993.He G Yu,Zhou Y B,Zhang G F.Numerical Recipes in Fortran 77(in Chinese).Beijing:Science Press,1993.
[21]Raiche A. 3DEM modeling using integral equation algorithm,AMIRA Project Report P223E,2001.

