贝叶斯网络在半导体设备故障诊断中的应用

郝晓亮

(中国电子科技集团公司第十三研究所，河北石家庄 050051)

科技的进步带动了半导体行业的快速发展，半导体工艺越来越复杂，对设备可靠性的要求也越来越高，设备也在朝着大型化、自动化、智能化、集成化方向发展。设备中的各个部件之间关系复杂，设备一旦出现故障，会对整个生产线造成重大影响。如何能够快速地确定并解决设备的故障，越来越受到人们的关注。人工智能和计算机技术的快速发展给故障诊断指出了一个发展方向，即智能故障诊断。目前有很多智能诊断的方法：故障树分析法、神经网络系统、智能专家系统、马尔科夫可靠性模型、概率因果网络、贝叶斯网络等。

由于设备的复杂性，知识的不完备性，以及检测手段的局限性，使得设备的故障诊断具有很大的不确定性。在故障诊断领域，不确定性是一个普遍现象。贝叶斯网络以其在处理不确定性问题的强大能力，丰富的概率表达能力越来越受到人们的重视[1]。

1 贝叶斯网络概述

贝叶斯网络（Bayesian Network）又称贝叶斯信念网络，是描述随机变量（事件）之间依赖关系的一种图形模式，是目前不确定性知识表达和推理领域最有效的理论模型之一[2]，适用于不确定性和概率推理的知识表达和推理[2]。

贝叶斯网络由两部分构成，一是贝叶斯网络结构图，另一部分是条件概率表（Conditional Probability Table，CPT）。

1.1 贝叶斯网络结构图

贝叶斯网络结构图是一个有向无环图（Directed Acylic Graph，DAG）[2]，是贝叶斯网络的定性表示。图中的节点表示事件中的变量，节点之间用有向弧线连接，弧线指向的是子节点，弧线的另一端是父节点，表示的是两个事件的因果关系。没有任何弧线指向的节点是根节点。

1.2 条件概率表

条件概率表是贝叶斯网络的定性表达，表示的是网络中各个节点之间的影响程度，是用概率分布来表示的，由一系列的概率值组成。

1.3 贝叶斯定理

贝叶斯网络的理论基础是贝叶斯定理，贝叶斯网络是在贝叶斯定理基础上发展起来的用于系统的描述和解决概率问题的图形，可以从事件发生的结果去反推引起事件发生的各个原因的概率大小。在故障诊断时，最常见的问题是已知故障发生，要寻找故障发生的原因，即“执果寻因”。因此，贝叶斯定理在故障诊断领域应用广泛。

贝叶斯定理:设实验E的样本空间S。A为E的事件，B1B2，...Bn为S的一个划分，且P(A)>0，P(Bi)>0(i=1，2，...n)，则

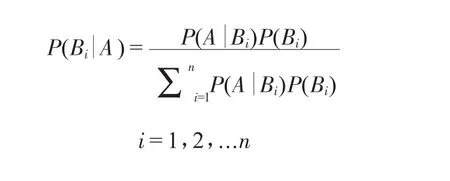
1.4 贝叶斯网络故障诊断中常用的概念

这里介绍贝叶斯网络故障诊断技术中常用的几个概念：先验概率，后验概率，条件概率，条件独立性假设。

先验概率

先验概率是人们事先对事件发生的概率大小的估计，该类概率是人们估计的概率，没有经过验证，是检验前的概率，称之为先验概率，通常是由领域内的专家或根据设备的历史资料来确定。

后验概率

后验概率是人们在经过调查等方式取得了新的证据，再利用贝叶斯公式，计算出的更接近于实际情况的概率。

条件概率

设A、B是两个事件且P(A)>0，则称概率

为事件B在事件A发生下的条件概率。条件独立性假设

设有随机事件A、B、C，如果A、B关于C条件独立，则有

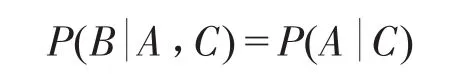
这说明，在事件C发生的条件下，事件A的发生与否，与B无关。条件独立性假设能简化网络推理的过程，还能大大减少网络推理所需要的先验概率的数量。

2 贝叶斯网络的故障诊断原理

假设事件A、B是导致事件C发生的两个原因，假设事件A发生的概率是0.2；事件B发生的概率是0.4；事件A发生，B也发生时，事件C发生的概率是0.95；事件A发生，事件B不发生时，事件C发生的概率是0.8；事件A不发生，事件B发生时，事件C发生的概率是0.9；事件A、事件B都不发生时，事件C发生的概率是0.1；即：

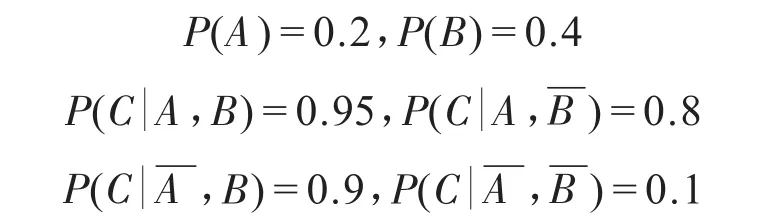
此事件的贝叶斯网络结构图如图1、图2所示。

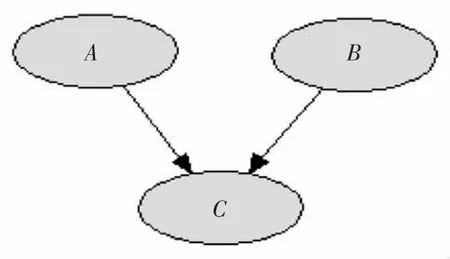
图1 贝叶斯网络结构图

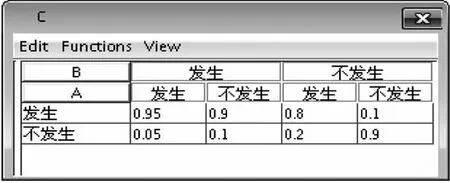
图2 事件C的条件概率表

在已知的条件下，计算如果事件C发生，事件A、事件B发生的概率。先计算事件A发生的概率。

根据贝叶斯定理

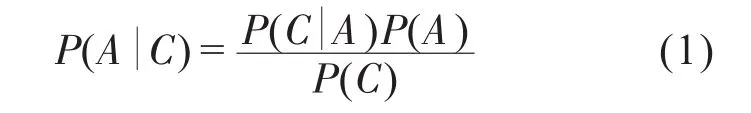
其中，P(C)是在不考虑事件A、B的是否发生，事件C发生的概率，可以用全概率公式计算：

将上面计算的数据代入到公式(1)中，得：

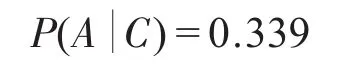
同理可以得出：

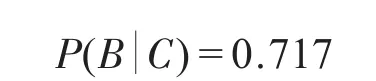
通过以上的分析可以得知，在已知事件C发生的情况下，事件B发生的概率要比事件A要大。这种分析方法可以应用于故障诊断领域，在故障诊断领域，常见问题是已知了设备的故障，想找到引起故障的原因，利用贝叶斯网络故障诊断技术，可以方便的知道引起设备故障的各个原因的概率。根据这个概率的大小来指导下一步的维修。贝叶斯网络故障诊断的原理就是“执果寻因”，通过已知的证据以及先验概率，利用贝叶斯定理来计算在已经故障（证据）的前提下，引起故障的各个原因的条件概率的大小。

3 贝叶斯网络故障诊断的过程

目前在贝叶斯网络故障诊断领域常用的模型是故障—征兆（Failure-Symptom）模型。在此模型中，根据网络中各个节点的性质分为故障原因节点和故障征兆节点。故障原因节点是导致故障发生的最根本的原因，通常不容易观察和检测。故障征兆节点通常可以通过观察、测量或检修等操作确定该节点的状态，此节点的状态可以作为证据输入到网络中。

贝叶斯网络故障诊断过程通常有以下几个步骤：

（1）将整个事件中的子事件列出，这些就是网络中的节点，根据节点的性质分为故障原因节点和故障征兆节点。

（2）确定贝叶斯网络中各个节点之间的关系，网络中节点之间的因果关系通常由领域内的经验丰富的专家，或者根据设备的历史资料确定。

（3）给定各个节点的条件概率表。这些概率都是先验概率，包括故障原因节点的概率以及故障征兆节点在故障原因节点状态已知下的条件概率。确定方法前文已经说过。

（4）通过观察、检测、检修故障征兆节点确定一个证据。

（5）将证据输入到贝叶斯网络中，利用贝叶斯定理，结合网络结构和条件概率表，计算各个节点在已知证据下的条件概率值，根据计算出的结果，找出概率最大的节点。

（6）检测并修复概率最大的节点，如果故障排除，诊断结束。如果故障未排除，此节点的状态信息就是另一个证据。返回第5步。直到找出故障的真正原因。

通过贝叶斯网络的故障诊断可以计算出出现故障后，引起故障的各个原因的概率值，通过这些概率值可以指导下一步的维修操作。

4 贝叶斯网络故障诊断在RIE维修中的应用

刻蚀工艺在半导体工艺中所起的作用越来越大。刻蚀技术分为干法刻蚀和湿法刻蚀，其中干法刻蚀凭借其均匀性好，控制精度高等优点，被广泛采用。干法刻蚀技术主要有反应离子刻蚀（RIE）和感应耦合等离子体刻蚀（ICP）。本文以RIE刻蚀机为例，介绍一下贝叶斯网络故障诊断技术在半导体设备故障诊断中的应用。

RIE主要由以下几部分构成：真空系统，反应气体及控制系统，射频电源，匹配网络等。在RIE的维修中，最常见的故障是设备无法起辉，无法产生等离子体。引起此故障的原因很多：反应气体的进气量、真空室的真空度、射频电源、匹配网络、腔体的洁净度等。各个原因之间关系错综复杂，给维修带来了很大的麻烦。利用贝叶斯网络故障诊断技术，可以将这些故障原因图形化，并利用这些图形结构以及各个故障之间的条件概率，计算各个故障原因的概率。

4.1 贝叶斯网络的构建

通过分析引起此次故障的可能的原因，以及各个原因之间的联系，确定网络中的节点类型以及节点之间的联系。再给定各个节点的条件概率表。这通常是个复杂的过程，为了确保贝叶斯网络的精确性，可以咨询领域内经验丰富的专家，再结合设备的具体情况以及设备的历史资料等来综合确定。图3是RIE无法起辉的贝叶斯网络结构图。条件概率表由于比较复杂不再列出。

4.2 贝叶斯网络的诊断过程

在图3中可以看出，里面包含很多个节点，每个节点之间的关系错综复杂。要计算各个节点的后验概率是个复杂和困难的过程。结构越复杂，节点越多，运算越复杂。

为解决这个问题，一些科研机构和公司开发了一些贝叶斯网络的开发工具，本文中所用的工具是Hugin Expert软件，这是一款基于贝叶斯网络的分析决策软件。本文中贝叶斯网络的构建及运算都是利用这个软件完成。

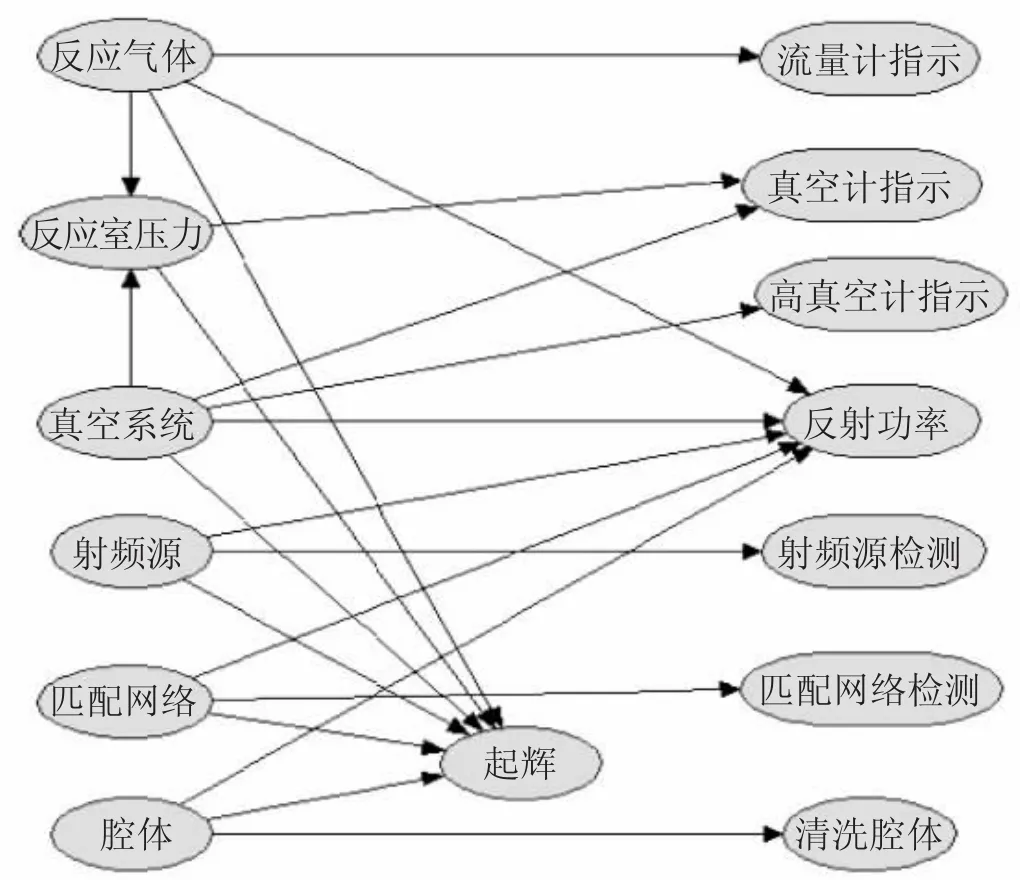
图3 RIE无法起辉的贝叶斯网络

贝叶斯网络在进行故障诊断时，各个节点的概率会随着证据的加入而发生变化，需要根据在取得证据后的概率，进行下一步的操作。图4列出了各个节点的概率值，图中所示的是百分数。当前已知的是设备起辉不正常，将这个作为证据，加入到网络中，经过计算，得出如表1的概率排列。

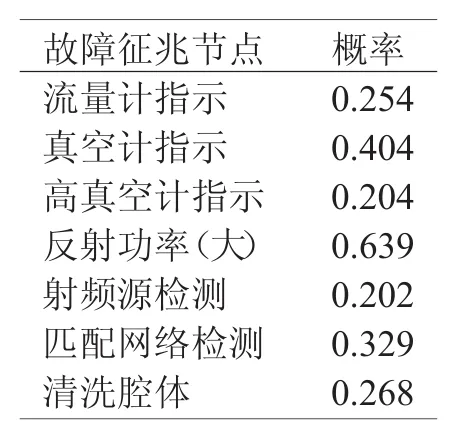
表1 RIE无法起辉下的故障征兆节点概率

如表1所示，此时反射功率大的概率是最大的，检查反射功率如果反射功率大，将此作为另一个证据输入到网络中，重新计算。计算结果如表2

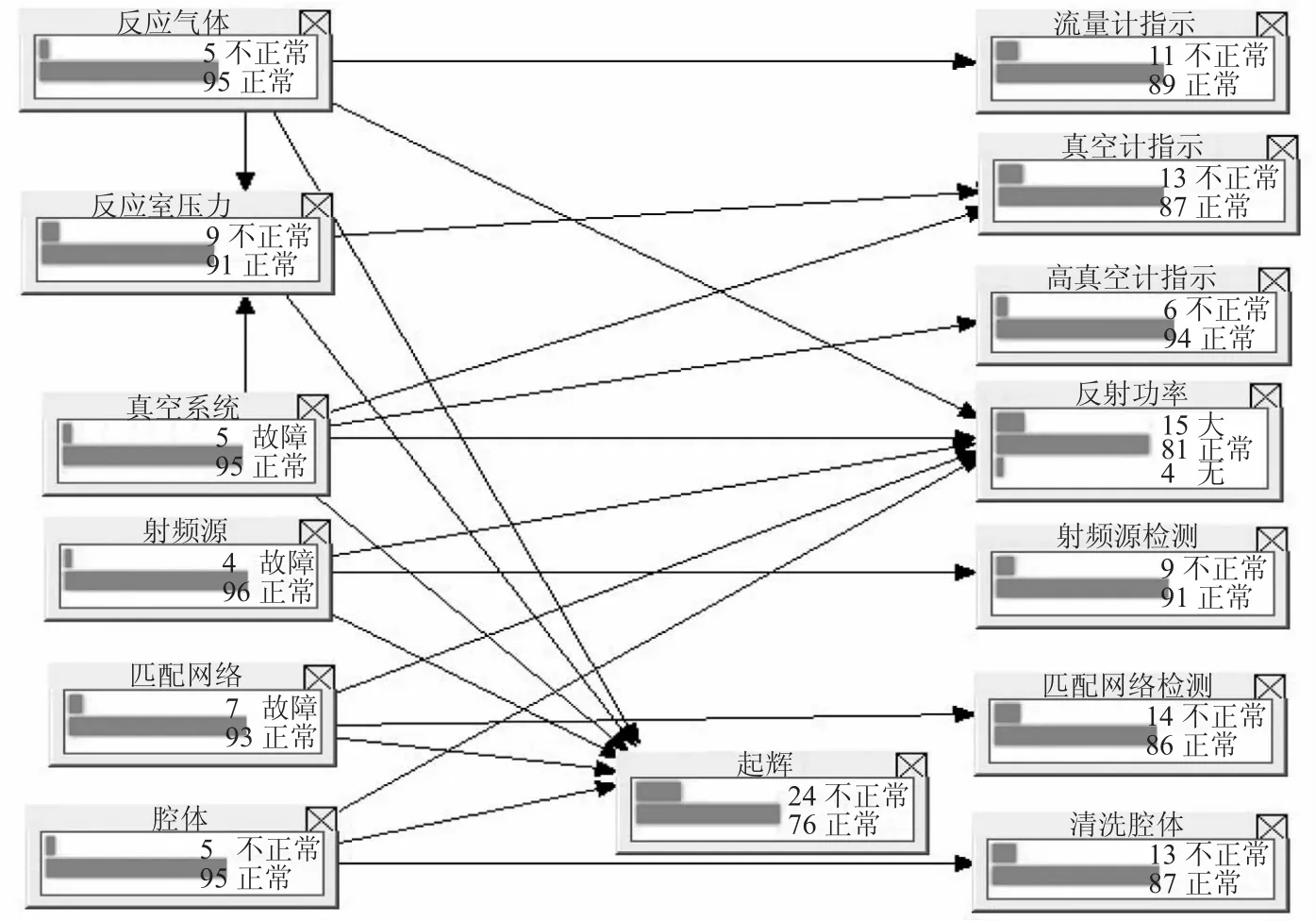
图4 RIE无法起辉贝叶斯网络节点的概率

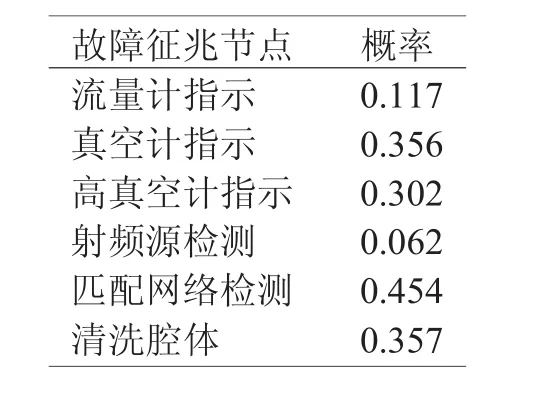
表2 设备不起辉和反射功率偏大条件下征兆节点的概率

通过上述的分析过程可以看出，在RIE的故障检测中，以贝叶斯网络计算出的各个节点的概率为指导进行维修，可以减少很多的分析过程，节约大量的时间。设备越复杂，贝叶斯网络的作用越明显。

在实际维修中还应该综合考虑维修成本、维修时间等因素，具体可参看有关文献[3]，本文不再赘述。

5 结 论

本文介绍了贝叶斯网络故障诊断技术在RIE刻蚀机维修中的应用，贝叶斯网络完全可以应用到更复杂系统的故障诊断中。贝叶斯网络自身还有学习的功能，能将先验概率的依赖降到最低，提高诊断的精度。故障诊断是贝叶斯网络的一个应用，贝叶斯网络还有很多其他的应用，目前被广泛应用于辅助智能决策、医疗诊断、数据挖掘等领域。

[1] 李俭川，胡茑庆，秦国军，温熙森.贝叶斯网络及其在设备故障诊断中的应用，中国工程机械，2003，10（5）：896-900.

[2] 张兵利，裴亚辉，贝叶斯网络故障概述，电脑与信息技术，2008，16（5）:41-42

[3] 赵春华，严新平，赵新泽.基于贝叶斯网络的内燃机故障诊断研究，武汉理工大学学报，2005，29（3）：334-338

[4] Jensen F V，Bayesian Networks and DecisionDiagrams，New York:Springer，2001.

[5] Friedman N，Geiger D，Goldzmidt M.Bayesian Network classifiers[J].Machine Learning，1997，29(2-3):131-163.