多状态串并联系统工作性能及其状态概率分析

古莹奎， 邱光琦， 储 茜

（江西理工大学机电工程学院，江西赣州341000）

0 前 言

大多数情况下， 系统是由多个具有多种状态的且功能各异的组件构成. 各组件之间关系复杂，对系统性能的影响也不尽相同. 由于组件性能退化的机理存在差异性， 使系统及其组件都可能呈现出多种工作状态和多个失效模式. 因而，系统的性能及状态取决于其组成部件的结构关系、性能及状态[1-3]. 传统的二态系统仅考虑系统和组件的两种可能状态：最佳状态和完全失效，显然不能适应对这种含有多状态组件的多状态系统进行性能分析[4-5]. 多状态系统理论的发展为解决此类问题提供了有力的支持[6]. 串并联系统是一种常见的典型系统结构，目前对多状态串并联系统的分析研究主要集中在系统的可靠性评估和结构优化方面，如Agarwal 和Sharma 等都对多状态串并联系统的同质冗余分配问题进行了研究， 分别采用启发式算法和蚂蚁克隆算法来求解优化问题[7-8]；Li 和Tian等基于物理规划和遗传算法对多状态串并联系统的可靠性评估以及组件设计优化进行了研究[9-10]；Nourelfath 等研究了在维修方针下的多状态串并联系统优化设计方法[11]；Levitin 应用通用产生函数法对多状态串并联系统的优化进行了系统的研究[5].以上研究着重于对系统可靠度和状态概率的分析计算，而较少对系统在各个不同状态下的性能水平进行分析. 文中综合考虑多状态串并联系统的状态和该状态下的性能水平，应用等同集的概念探讨其不同状态组合下的发生概率和性能水平以及系统整体性能水平的计算方法，以求为系统的风险评价、可靠性评估和预防维修提供理论支持.

1 多状态系统的结构函数和等同集

对于含有n 个多状态组件的多状态系统，系统可以有M+1 个状态：[0，1，2，…，M]，其中状态0 代表完全失效状态，状态M 代表完好状态，其余代表中间状态. xi（i=1，2，…，n）代表第i 个组件的状态，每个组件可以有mi+1 个状态：[0，1，2，…，mi]，其中状态0 代表完全失效状态，状态mi代表完好状态.系统状态与组件状态之间的映射关系可以用结构函数φ（x）来描述， x=（x1，x2，…，xn）为组件状态向量[4,12].

由此可见，多状态系统的状态包含大量的组件状态集合. 对于含有不同组件状态向量的系统状态，如果其中某个或某几个组件状态的变化并未使系统的状态发生变化，则认为包含这个或这几个组件状态的集合属于同一等同集，隶属于同一状态.

2 多状态串并联系统性能与状态概率分析

2.1 多状态串并联系统结构分析

图1 多状态串并系统结构图

系统的可靠性水平可以用组件概率分布矩阵P 来描述为：

式（2）中，pij（i=1，2，…，ns，j=0，1，2，…，M）表示第i个组件在第j 个状态的概率.

系统的性能水平可以用组件性能分布矩阵U来描述为：

式（3）中，uij（i=1，2，…，ns，j=0，1，2，…，M）表示第i个组件在第j 个状态下的性能水平.

2.2 多状态串联系统的可靠性及性能分析

若多状态系统是串联结构， 则系统处于第j 个状态或者更高一级状态的必要条件是当且仅当每一个组件的性能都等于或大于给定的性能值uj，uj+1≥uj（j=0，1，2，…，M-1），也就是说，多状态串联系统的性能即是系统中最差状态组件的性能.

若以P （Sk） 表示系统在状态k 时具有性能uk的整体概率，则有：

2.3 多状态并联系统的可靠性及性能分析

若多状态系统的结构是并联的，则并联系统处于第j 个状态或更高状态的充分条件是至少有一个组件的性能等于或大于给定的性能值uj，uj+1≥uj（j=0，1，2，…，M-1），也就是说，多状态并联系统的性能为系统中最佳状态组件的性能.

设并联结构由n 个组件构成，系统在第k 个状态时的等同集为Sk. 给定并联系统在第k 个状态时的性能水平uk，由并联系统的性质可以知道，该状态下系统可能具有多个性能水平uj，uj≥uk（j=1，2，…，J），则其等同集又可以据此划分为J 个子集，表示为：

对每一个性能水平uj（j=1，2，…，J ）所对应的等同子集，设其含有j（n）个部件状态组合，则在该性能水平下的系统状态概率为：

由此， 可得系统在状态k 下具有性能uk的整体概率为：

基于并联系统的定义，同一状态k 下系统可能具有多个不同的性能水平， 因而系统在该状态下的总体性能应为各个不同性能的加权平均性能，以u（Sk）表示如下：

2.4 多状态串并联系统可靠性及性能水平分析

对于如图1 所示的多状态串并联系统来说，系统处于第j 个状态或者更高状态的必要条件是在每个并联子系统中至少有一个组件的性能等于或者大于给定的值uj，uj+1≥uj（j=0，1，2，…，M-1），也意味着每一个子系统必须是处于第j 个状态或者更高的状态.

由于多状态并联系统的性能定义为系统中最佳状态组件的性能，多状态串联系统的性能定义为系统中最差状态组件的性能，因此多状态串并联系统的系统性能定义为[13]：

式（10）中，uij是第j 个组件在第i 个子系统中的性能，u 是一个在多状态串并联系统中表示所有组件性能的矢量.

根据多状态系统的定义， 系统在第j 个状态（j=0，1，…，M）或者更高状态的概率为：

式（11）中，u 是系统中表示所有组件性能的矢量，φ（x）是系统的结构函数，φ（x）＝0,1,2,…，M. γ（u）是系统性能函数，ui表示所有组件在第i 个并联子系统中的性能，γi（ui）是第i 个并联子系统的性能函数，uj是预先给定的性能值.

式（11）说明系统是存在第j 个状态或更高状态的，系统性能不应该低于额定值uj，所以每一个并联子系统的性能都不应该低于uj. 式（11）同时也表明，多状态串并联系统的可靠性是其多状态组件性能分布矩阵U 和可靠性分布矩阵P 的函数，表示为：

为了计算系统的可靠性，需要计算每一个并联子系统的可靠性. 给定φi（xi）是第i 个并联子系统的结构函数，子系统处于第j 个状态或者更高状态的可靠性表达为：

式（12）中，ni是第i 个并联子系统的组件数，uir是第r 个组件在第i 个并联子系统之中的性能.

基于以上分析，可以得到整个系统的性能水平Us，表示为：

式（14）中，Us为系统性能，Uj为系统处于第j 个状态时的加权平均性能，Pr（φ（x）＝j）为系统处于第j个状态时的概率.

3 多状态串并联系统性能与状态分析及其维修决策框架

基于以上方法对多状态串并联系统进行分析，在获取系统工作性能及其状态概率后，可以为系统性能的动态评估以及维修决策提供理论支持，框架如图2 所示.

图2 多状态串并联系统性能与状态分析及其维修决策框架

（1）为系统性能的动态评估提供支持. 系统在运行过程中，性能处于逐步退化中，随着性能的退化，其状态也从高状态向低状态迁移，在这个过程中，系统并没有发生失效，因而没有可用的可靠性数据来对其运行可靠性做出动态的评估. 但可以通过对表征系统组件性能的主要特征参数进行监控，获取其动态性能值，通过定义组件性能区间与其状态的对应关系可以确定其隶属的状态；由于系统组件性能的退化一般是遵循一定的分布规律，按照一定轨道进行的，通过分析可获取该性能水平下的发生概率. 在获取系统各个组件的性能以及工作状态概率后可对系统的性能和状态做出动态的评估.

（2）为系统的维修提供支持. 系统运行到一定的时间或性能退化接近或达到一定的阈值时，为保证系统运行的安全性，需要停机进行维修. 预设性能阈值，通过对系统状态和性能的动态评估，可以找到最佳停机维修点，从而节约维修资源，减少停机成本和减少事故发生的几率.

4 实例分析

以某钢铁集团炼钢厂转炉全悬挂倾动装置二级减速机系统为研究对象，应用提出的方法分析其状态和性能水平. 在实际工作过程中，二级减速机系统的失效是一个从完好状态到完全失效状态的时序过程，整个系统具有多状态性，是一个典型的具有多状态组件的多状态系统，每台减速机有自己不同的工作状态和相应状态下的性能水平. 为不失一般性，考虑设备由于维修维护状况、工作位置和工作环境的不同，每台减速机的状态和工作性能各异. 转炉倾动装置传动系统如图3 所示，其中四台二级减速机构成串并联结构，如图4 所示. 二级减速机的工作状态对倾动系统的工作性能有着重要的影响，对倾动系统的安全性、平稳性和可靠性有着重要的作用.

图3 全悬挂转炉倾动装置图

图4 二级减速机配置示意图

表1 各二级减速机性能及状态分布

若给定系统3 个性能水平u0=0.1，u1=0.3，u3=0.5. 枚举各个状态下的等同集，并依据系统性能水平对等同集进行分组，计算各等同集及各状态组合的等同概率和系统概率，如表2～表4 所示.

表2 二级减速机串并联系统在0 状态时的性能分布

由表2 可知，二级减速机串并联系统在0 状态时，等同集包含25 个状态组合，系统性能可能为0或0.1，其概率为0.007 488+0.004 975=0.012 462 5，其中系统性能为0 的概率为0.007 488， 系统性能为0.1 的概率为0.004 975. 由式（9）可得系统平均加权性能为：

（0.007 488*0+0.004 975*0.1）/0.012 462 5=0.039 920

表3 二级减速机串并联系统在1 状态时的性能分布

从表3 可以知道，二级减速机串并联系统在1状态时， 等同集包含39 个状态组合， 其概率为0.068 462 5+0.342 362 5=0.410 825. 在该状态下，系统具有两个性能水平，其中系统性能为0.3 的概率为0.068 462 5， 系统性能为0.4 的概率为0.342 362 5. 由式（9）可得系统的加权平均性能为：

（0.068 425*0.3+0.342 362 5*0.4）/0.410 825 =0.383 335

从表4 可以知道， 二级减速机多状态系统在2状态时， 等同集包含17 个状态组合， 其概率为0.576 712 5，状态性能为0.5.

基于以上分析，二级减速机串并联系统状态与性能分布如表5 所示. 系统处于状态0 的概率为0.012 462 5，平均性能为0.039 920；处于状态1 的概率为0.410 825 0，平均性能为0.383 335；处于状态2 的概率为0.576 712 5，平均性能为0.5.

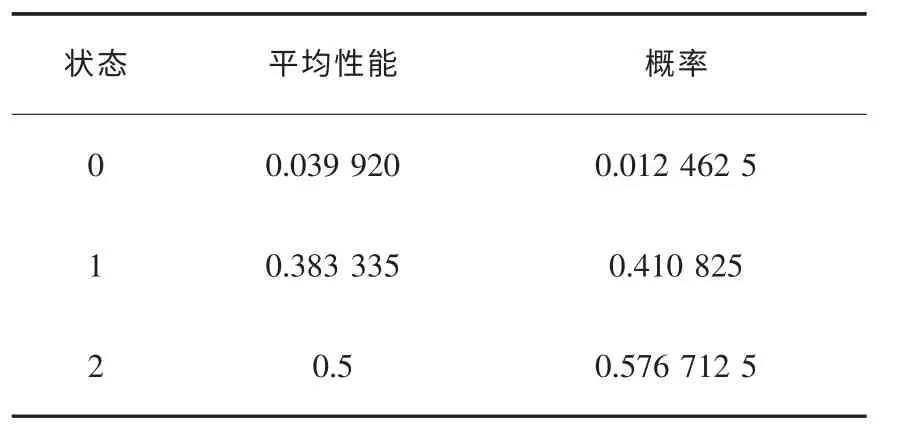
表5 二级减速机串并联多状态系统的状态分布

由式（14），可以得到整个系统的性能水平为：

即在四台二级减速机当前的状态下，用传动效率表征的二级减速机系统的总体性能为0.446 337.假若设定系统的性能应不低于0.5， 由于系统实际性能低于该设定值，必须对系统停机并实施维修.

5 结 语

文中在对多状态串并联系统结构关系分析的基础上，分析其工作状态和性能水平. 由于多状态系统性能与其组件的结构关系及状态组合直接相关，探讨了多状态串联系统、并联系统及串并联系统处于某个状态或者更高状态的充分必要条件，应用等同集的概念分析不同性能水平下系统组件状态组合的概率和整体状态概率，得到该状态下系统的平均加权性能，并进一步计算整个系统的性能水平. 据此分析结果可以为系统的可靠性与性能评估以及维修决策提供理论支持.

[1] 周金宇，谢里阳. 多状态系统共因失效机理与定量分析[J]. 机械工程学报，2008，4(10): 77-82.

[2] 高 鹏， 谢里阳. 基于改进发生函数方法的多状态系统可靠性分析[J]. 航空学报，2010，31(5): 934-939.

[3] 古莹奎，朱繁泷，唐淑云. 基于模糊概率重要度的发动机可靠性分析[J]. 江西理工大学学报， 2012，33(5): 51-55.

[4] Linsinaksi A, Levitni G. Mutli-state system reliability: assessment,optimizationandapplications[M].Singapore:WorldScientificPublishing Company, 2003.

[5] Levitin G. The universal generating function in reliability analysis and optimization[M]. London: Springer-Verlag, 2005.

[6] Gu YK, Li J. Multi-state system reliability: A new and systematic review[J]. Procedia Engineering, 2012, 29: 531-536.

[7] Agarwal M, Gupta R. Homogeneous redundancy optimization in multi-state series-parallel systems: A heuristic approach [J]. IIE Transactions, 2007, 39 (3): 277-289.

[8] Sharma V K, Agarwal M, Sen K. Reliability evaluation and optimal design in heterogeneous multi-state series-parallel systems[J].Information Sciences, 2011, 181(2): 362-378.

[9] Li W, Zuo M J, Moghaddass R. Optimal design of multi-state weighted series-parallel systems using physical programming and genetic algorithms [J]. Asia -Pacific Journal of Operational Research, 2011, 28(4): 543-562.

[10] Tian Z, Levitin G, Zuo M J. A joint reliability –redundancy optimization approach for multi-state series–parallel systems[J].Reliability Engineering and System Safety, 2009, 94 (10): 1568-1576.

[11] Nourelfath M, Ait-Kadi D. Optimization of series-parallel multistate systems under maintenance policies[J].Reliability Engineering and System Safety, 2007, 92 (12): 1620-1626.

[12] Ding Y, Lisnianski A. Fuzzy universal generating functions for multi-state system reliability assessment [J]. Fuzzy Sets and Systems, 2008, 159(3): 307-324.

[13] Li W. Reliability evaluation and optimal design of multi-state weighted systems[D]. Edmonton: University of Alberta, 2008.