下行多用户CoMP系统资源分配算法

阔永红，万仁勇，陈健，王健

（西安电子科技大学 通信工程学院，陕西 西安 710071）

1 引言

在新一代无线通信网络中，协作多点传输和接收(CoMP, coordinated multi-point transmission and reception)作为消除邻小区干扰、改善小区边缘用户性能和提高频谱效率的一种重要手段，得到了广泛的关注[1～3]。在基于MIMO-OFDMA的CoMP系统中，通信信道被分解成多个空间和频率上并行的平坦衰落子信道，适合传输高速数据流[4]。

近年来，下行CoMP系统资源分配算法的研究主要集中在速率自适应 (RA, rate adaptive)方面[5～7]。文献[5]研究了在单基站功率受限时将凸优化技术应用于线性预编码和功率分配的联合优化以提高传输速率；文献[6]研究了在单基站功率和总基站功率分别受限时传输速率的最大化问题；文献[7]通过联合非线性预编码和功率分配来提高总的传输速率。但以上工作均是致力于最大化系统吞吐量，而一些实际系统中希望尽可能地降低发射功率，因此有必要研究边值自适应(MA, margin adaptive)问题[8～11]。文献[8]研究了迫零波束赋形下的多用户MIMO-OFDMA系统，将联合优化问题分解成3个子优化问题，有效地降低了算法的复杂度；文献[9]利用拉格朗日对偶算法最小化发射功率，获得了最优的系统性能；文献[10]提出了一种基于用户分组的子载波分配算法。文献[8,10]算法的性能损失较多，文献[9]算法的复杂度较高。

本文针对多用户CoMP系统中的MA问题提出了一种新的资源分配算法：由用户最低速率要求及平均信道增益粗略计算出每个用户所需要的子载波数目后，提出根据空间子信道增益最大化和用户公平性原则进一步分配子载波，进而最小化总发射功率；提出通过预设判决门限、剔除较差的空间子信道，实现快速的比特加载，并解决了比特整数性问题。仿真结果表明，所提算法在满足用户最低速率和误码率的前提下，降低了总的发射功率和算法复杂度，性能接近最优算法。

2 系统模型和预编码

2.1 系统模型

图1描述了一个下行多用户CoMP(MU-CoMP,multiple user CoMP)系统，包含一个中央控制单元、I个协作基站以及K个用户。中央控制单元充当无线网络控制器(RNC, radio network controller)[5]，负责共享协作用户的信道信息和数据信息，进行发射端预编码，集中实施多用户CoMP系统的资源分配算法。

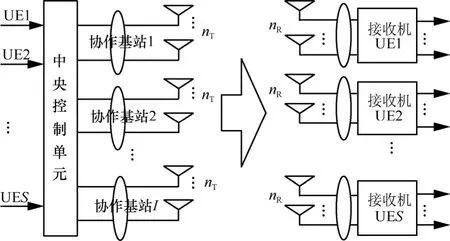
图1 下行MU-CoMP系统模型

假设每个基站和用户分别配备nT、nR根天线，系统子载波数目为M，每个子载波上同时传输的协作用户集合为：，假设S1,S2,…,SM集合中的用户数目均为S(S＜K)。此时MU-CoMP系统等效成为一个NT×NRm维的虚拟MU-MIMO系统[3,5,6]，且NT≥NRm。

协作基站端的发射天线总数为

子载波m上用户集合的接收天线总数可表示为

因此，子载波m上用户jk的接收信号可表示为[3,5]

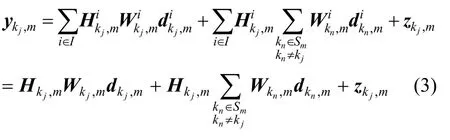
其中，等号右边的第1项表示有用信号，第2项表示来自其他用户的同频干扰，第3项为白噪声。其中，Hkj,m、Wkj,m、dkj,m分别表示用户kj在子载波m上的信道矩阵、预编码矩阵、数据向量，zkj,m表示均值为0、方差为σ2的复高斯白噪声信号。

2.2 预编码

MU-CoMP系统一般采用线性预编码消除下行多用户系统中的共信道干扰[5,12]。为了使发射端有足够的零空间消除所有用户之间的干扰，协作基站和协作用户的天线数必须满足以下关系：TRmNN≥，即发射天线总数不小于接收端的天线总数[9]。

Step1 子载波m上有S个协作用户同时传输，为了消除用户间的同频干扰，要求式(3)中等号右边的第2项为0，即

用户jk的干扰信道矩阵表示为

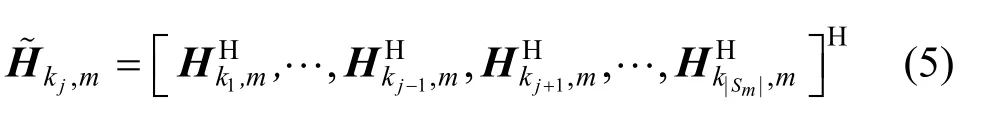
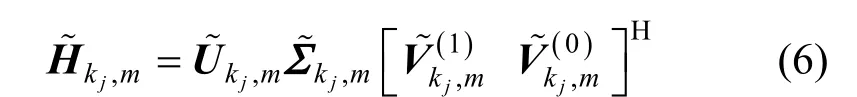
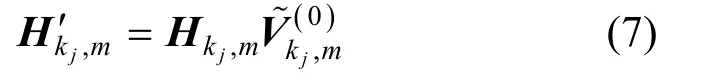
Step2 再次进行奇异值分解，将Hk′j,m分解成一系列并行无干扰的空间子信道。

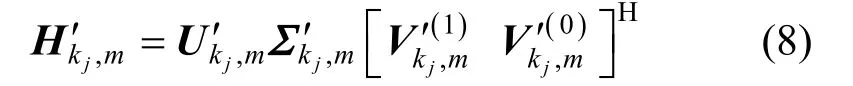
其中，Uk′j,m为酉矩阵，Σk′j,m为Lkj×Lkj维对角阵，对角线上的元素为Hk′j,m的奇异值，表示前Lkj列非零奇异值对应的列向量，其中，Lkj表示Hk′j,m的秩，即用户kj支持的数据流数目，1≤Lkj≤nR。

综上得到用户kj的预编码矩阵

3 多用户CoMP系统资源分配算法

3.1 数学模型

在满足用户最低速率要求的情况下，必须得到子载波分配和功率分配的最优解才能实现最小的发射功率。对于图1所示的MU-CoMP系统，总发射功率totp为

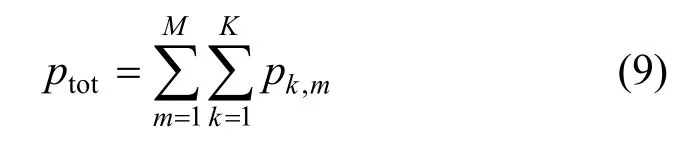
其中，,kmp为子载波m上用户k需要的功率，表示子载波m上用户k的第

3.2 低复杂度的有效资源分配算法

3.2.1 用户子载波数目确定

本文遵循以下原则来设计子载波分配算法，以尽可能地降低总发射功率[8,13]。

1) 在无线信道中，用户的平均信道增益越高，则在一定传输速率下所要求的发射功率越低；反之，则发射功率越高。

2) 更多的子载波应该分配给平均信道增益更小的用户以满足其速率要求，降低发射功率。

假设用户k在每个子载波上都经历相等的平l个空间子信道上的发射功率。若系统采用MQAM调制方式，,,kmlp可以表示为

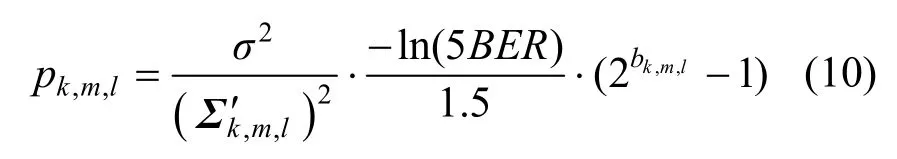
其中，σ2为高斯白噪声方差，BER为误码率，Σk′,m,l为等效信道矩阵Σk′,m对角线上第l个元素，大小取决于子载波分配的结果，bk,m,l为传输数据的比特数，表示系统冗余量，为了书写方便，后文用Γ代替。

每个子载波最多同时支持S个协作用户，用户的最低速率要求为minkR，本文优化问题的数学模型构建为

其中，ρk,m表示用户k是否使用子载波m，如果使用，则ρk,m=1；否则ρk,m=0。式(11a)表示每个子载波最多支持S个用户，式(11b)表示用户最低速率要求为Rkmin。

直接求解式(11)需要很高的复杂度。首先，不同用户在相同子载波上传输，发射功率pk,m是相互关联的，使得优化问题是一个联合优化问题；其次，由于式(10)的存在，优化目标(11)是一个非凸、非线性规划[10]。如果穷举出所有｛ρk,m｝组合，采用贪婪算法依次进行比特加载能够获得全局最优解，但是其计算复杂度是系统无法承受的[9]。

针对上述优化问题，本文分解成3步完成：1)根据用户的速率要求及平均信道增益来粗略计算出每个用户所需要的子载波数目；2)综合考虑用户的空间相关度和信道增益进行子载波分配；3)通过预判并剔除差的空间子信道实现快速比特加载。均信道增益，则它在每个子载波上的传输速率为Rk/mk，mk表示用户k分配的子载波数目，它在mk个子载波上消耗的总功率可表示为

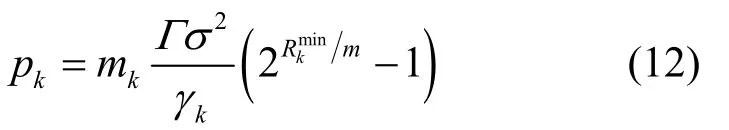
根据式(12)可知，本文采用基于信噪比的频谱分配 (BABS, bandwidth assignment based on SNR)算法[12]来确定用户的子载波数目。具体算法流程为

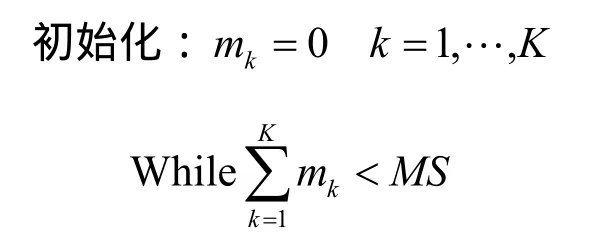
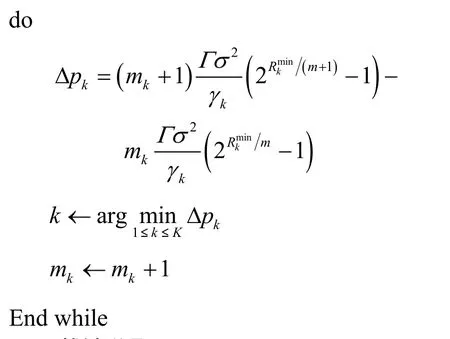
3.2.2 子载波分配

基于奇异值分解的预编码虽然能够消除用户之间的干扰，但同时也损害了有用信号。用户之间的空间相关度越高，对有用信号的损害越大，等效信道增益就越小[8,13]；另一方面，系统消耗功率的多少在很大程度上不是取决于信道较好的用户，而是取决于信道较差的用户。为此，提出了一种新的子载波分配算法：子载波分配时优先考虑信道较差的用户，同时要兼顾到信道较好的用户不能分配到太差的子载波以及空间相关度太高的用户不能共享一个子载波。下面给出算法的具体步骤。

Step1 求出每个子载波上用户两两之间的空间相关度矩阵R。

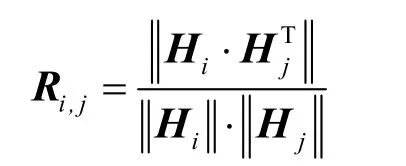
Hi和Hj为任意2个用户i和用户j对应的信道矩阵。取矩阵Ri,j内所有元素的均值，即为用户i和用户j之间的空间相关度。

Step2 为每个子载波选择其协作用户集合的第1个用户。

①将K个用户按照其平均信道增益值升序排列。

②根据用户排列的顺序，依次为每个用户分配一个子载波，对于剩余的M-K（M＞K）个子载波，按照同样的顺序再次分配，直到所有M个子载波均被分配了首个用户时结束，并记录各个子载波被分配给用户的先后顺序。

Step3 为每个子载波选择其协作用户集合的用户。

①按照Step2确定的顺序，依次为每个子载波找出所有满足以下条件的用户集合K′。

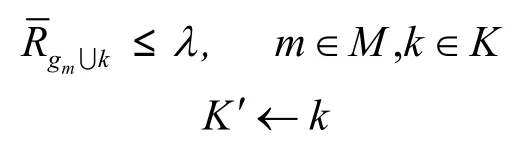
② 计算用户集合｛gm∪k｝的平均信道增益Hgm∪k，k∈K′，取

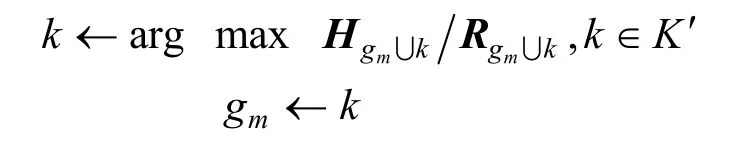
③ 重复②，继续为各子载波选择协作用户集合的用户，直到每个子载波上用户数目满足

Step4 每选择一个协作用户，都要检测该用户已经分配的子载波数目，数目满足mk的用户不再参与分配过程，同时更新R矩阵，直到所有的子载波分配完毕。

3.2.3 比特加载

子载波分配完毕之后，比特加载问题可以由传统的注水算法[9]或最优的贪婪比特加载算法[10]来确定，但这2种算法搜寻次数较多，复杂度较高，不适合传输高速数据，因此需要改进比特加载算法。

由上文可知，用户k所分配的子载波数目为mk，天线数目为nT，因此经过预编码之后得到的空间子信道数目为N=mknT,用户k第l（1≤l≤N）个空间子信道上的功率为pk,l,暂不考虑比特的整数性要求，最优的比特加载所得到的功率分配一定满足注水定理，因此pk,l可以表示为

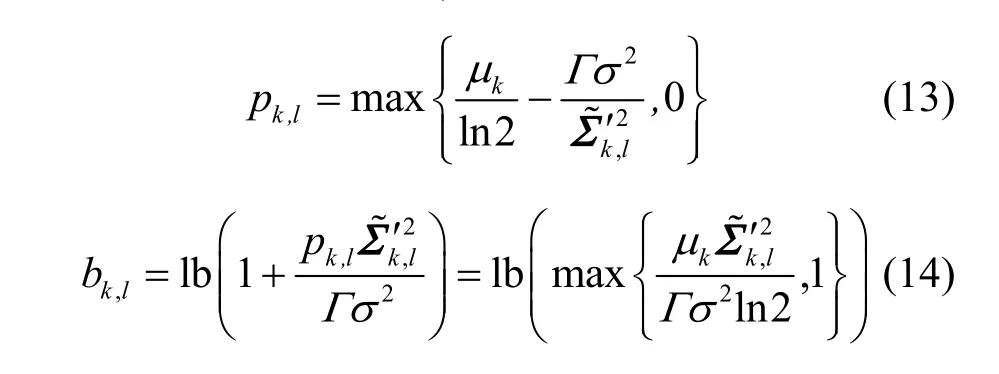
用户k第l个子信道上的等效信道增益。式(14)又可改写为

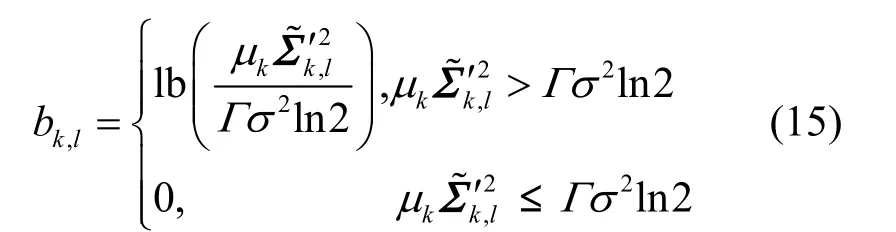
并且满足

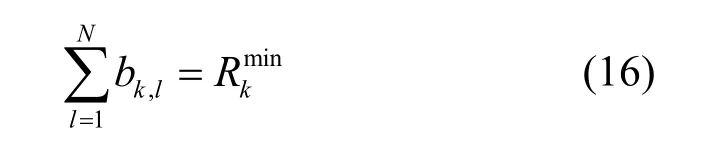
式(15)取零的时候表示该子信道不分配比特，因为其信道条件较差，不适合用来传输数据，因此将被剔除。如果笔者能提前确定哪些子信道被剔除，就可以直接利用式(15)和式(16)来进行比特加载，从而避免多次搜索最优比特或注水水位，提高比特的加载速度。下文重点讨论如何预判哪些子信道将被剔除。

假设用户的最低速率要求为R，空间子信道数目为N，根据贪婪比特加载算法的执行过程可知，如果最终存在要被丢弃的子信道p，则必满足

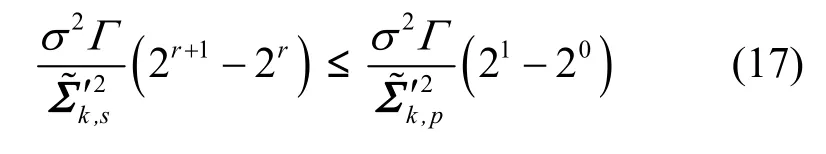
设定门限值为

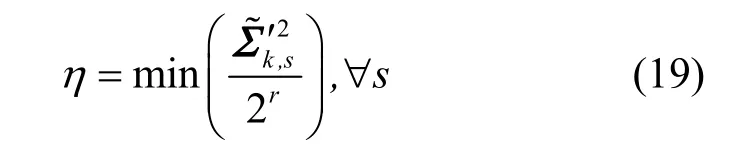
但由于s所代表的哪些子信道事先是不知道的，因此门限值也是无法精确确定的。在实际的算法中，采取如下的近似方案。

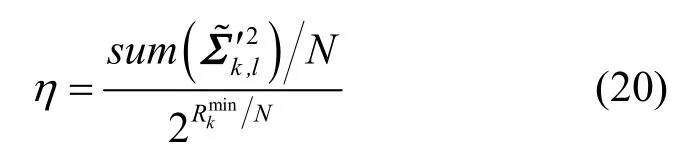
因此，如果某个空间子信道增益大于门限值η，则它可以用来分配比特；否则，剔除掉。

快速比特加载算法具体步骤如下。

Step1 利用式(20)确定将被剔除的空间子信道，利用式(15)、式(16)求出用户k在剩余空间子信道上分配的比特数目bk,l,l≤N′，N′表示剩余空间子信道数目。

4 仿真结果与分析

本节通过MATLAB仿真来验证所提算法的性能，蒙特卡洛仿真次数为200次。在仿真中，协作基站采用相同站址，协作基站数目I=3，用户数目K=12。采用nT=2,nR=2的MIMO-OFDM系统，信道模型采用EPA5低相关。子载波数目M=24，子载波频带宽度B=180 kHz ，每个子载波能够同时传输的用户数目为S=nTInR=3，假设用户具有相同的最低速率要求每个用户的空间子信道数目为N，具体数值取决于子载波分配结果。

为了分析、对比本文算法（即所提子载波分配算法和快速比特加载算法结合使用）的性能，笔者还仿真了下列4种算法。

1) SUS子载波分配[8]与贪婪比特加载算法相结合，文献[8]介绍了一种低复杂度的子载波分配方法，仿真时将它与最优的贪婪比特加载算法结合，以便对比资源分配的性能。

2) 文献[10]介绍的低复杂度资源分配算法。

3) 文献[9]算法由于在子载波数目16M≥ 时，该算法能够达到最优的系统性能，本文将此算法作为最优算法进行对比。

4) 本文所提子载波分配与贪婪比特加载算法相结合，这是为了对比本文的快速比特加载与最优的贪婪比特加载的性能。

图2给出了用户最低速率要求为100 bit/symbol时，5种算法需要的发射功率对比曲线。从图2中可以明显看出SUS子载波分配结合贪婪比特加载算法的性能最差，因为SUS子载波分配算法允许信道较好的用户优先选择协作用户，从而导致本来信道就差的用户为了满足自身的目标速率而消耗大量功率，抵消了信道较好的用户所带来的功率节省。文献[10]中算法的性能有所提升，文献[9]的性能最好。本文算法的性能仅低于文献[9]算法，但是所需要的计算复杂度比文献[9]大幅降低。另外，本文算法性能略低于所提子载波分配结合贪婪比特加载算法，说明所提的快速比特加载算法与贪婪比特加载相比性能损失很小。

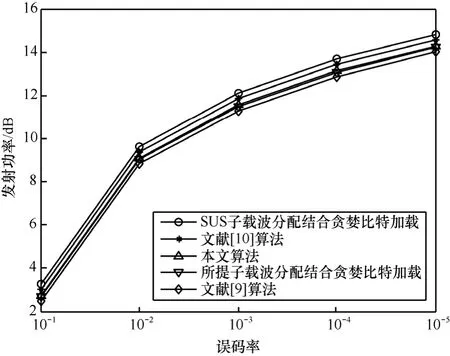
图2 最低速率要求为100 bit/symbol时，各种算法消耗的发射功率对比

表1给出了各种算法的总复杂度对比。本文算法及文献[9]、文献[10]采用块对角化预编码算法来消除同频干扰，所需复杂度为O(MS2nRNT2)[13]；基于ZFBF(zero-forcing beamforming)的SUS算法使用迫零算法来消除干扰，所需复杂度为O(MSnRNT2)[13]。表1中复杂度表达式的第2项表示子载波分配时对最优用户集合的搜寻次数，第3项表示贪婪比特加载时对最优空间子信道的搜寻次数或使用迭代注水算法分配功率时对最优注水水位的搜索次数。表1中文献[9]使用注水算法进行比特加载，itera表示迭代次数，在仿真中迭代4～6次即可趋近最优，计算时取5，用户速率R=100 bit/symbol，其他变量值在上文已给出。从表1中可以看到，所提子载波分配算法复杂度高于SUS及文献[10]中的方法，但小于文献[9]中的子载波分配算法。所提快速加载算法复杂度最小，因此综合后的资源分配算法以最小的复杂度获到了接近最优算法的性能，并且本文算法的复杂度与用户速率要求R无关，因此适合传输高速数据流的场合。

图3给出了误码率为10-4时，各种算法的发射功率对比，随着用户最低速率要求的提高，发射功率也随之增加，本文算法的性能总是接近最优算法。

表1 各种算法的复杂度比较

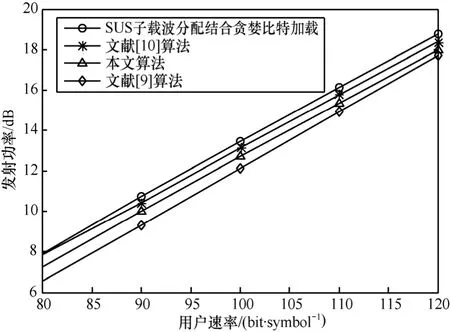
图3 误码率要求为10-4时各种算法消耗的发射功率

图4给出了误码率为10-4、最低速率要求为100 bit/symbol时，每个用户消耗的平均发射功率。仿真结果表明，本文算法每个用户需要的功率均值为2.15 dB；SUS子载波分配结合贪婪比特加载需要的功率均值为2.74 dB；文献[10]算法所需的功率均值为2.46 dB；文献[9]算法所需的功率均值为1.91 dB。由图4可知，与文献[9]中算法相比，本文算法的总功率低、各用户消耗的功率均衡。

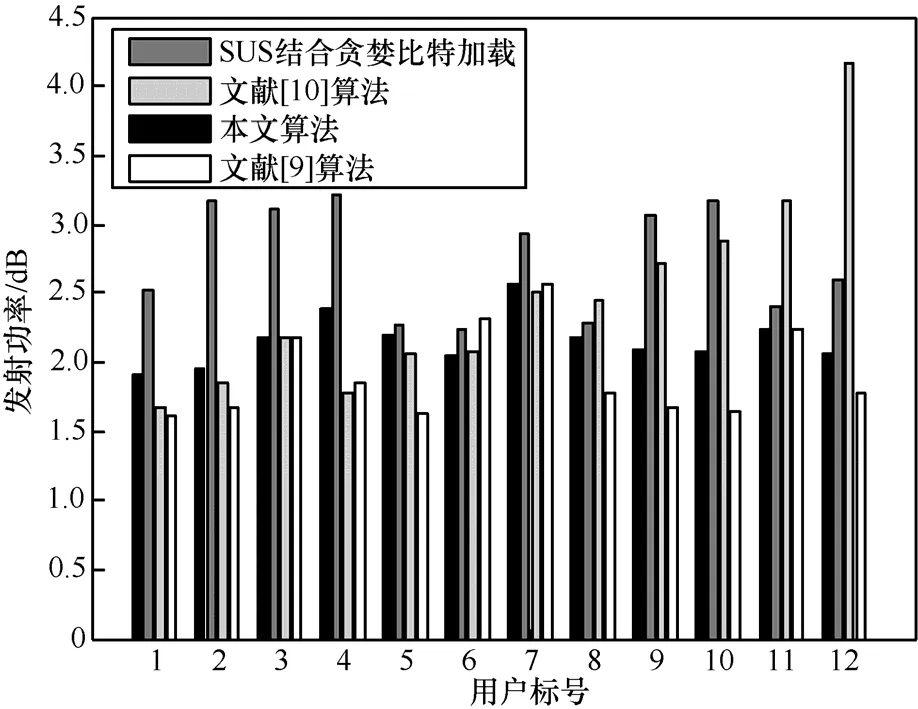
图4 误码率为10-4、最低速率要求为100 bit/symbol时，用户的平均发射功率

5 结束语

本文提出了一种下行多用户CoMP系统资源分配算法。该算法在满足用户误码率和最低传输速率要求的前提下将发射功率最小化问题分成3个步骤进行求解：根据用户的速率要求及平均信道增益来粗略计算出每个用户所需要的子载波数目；兼顾用户的空间相关度和信道增益分配子载波，均衡了用户的发射功率；通过预判并剔除差的空间子信道，实现快速的比特整数加载。本文算法以较低的复杂度和较好的性能，实现了满足用户最低传输速率要求下总发射功率的最小化。

[1] SAWAHASHI M, KISHIYAMA Y, MORIMOTO A, etal. Coordinated multipoint transmission/reception techniques for LTE-advanced[J].IEEE Wireless Communications Magazine, 2010, 17(3):26-34.

[2] GAO X Y, LIN A X, KAYAMA H. Low-complexity downlink coordination scheme for multi-user CoMP in LTE-advanced system[A]. International Symposium on PIMMRC[C]. Tokyo, Japan, 2009. 355-359.

[3] BATISTA R L, DOS SANTOS R B, MACIEL T F, etal. Performance evaluation for resource allocation algorithms in CoMP systems[A].IEEE VTC Fall[C]. Ottawa, Canada, 2010.1-5.

[4] 樊凌雁,何晨,冯国瑞. MIMO-OFDM系统下的自适应迭代比特分配算法[J]. 通信学报,2007, 28(11):65-70.FAN L Y, HE C, FENG G R. Adaptive iterative bit allocation algorithm for MIMO-OFDM system[J]．Journal on Communications,2007,28(11):65-70.

[5] CHOI D, LEE D, LEE J H. Resource allocation for CoMP with multi-user MIMO-OFDMA[J]. IEEE Transactions on Vehicular Technology, 2011, 60(9):4626-4632.

[6] ZHANG R. Cooperative multi-cell block diagonalization with perbase-station power constraints[J]. IEEE Journal on Selected Areas in Communications, 2010, 28(9):1435-1445.

[7] WIBOWO H, VUCETIC B, LI Y H. Multi-user cooperative base station systems with joint precoding and beam-forming[J]. IEEE Journal of Selected Topics in Signal Processing, 2009, 3(6):1079-1093.

[8] SHIN Y I, KANG T S, KIM H M. An efficient resource allocation for multiuser MIMO-OFDM systems with zero-forcing beamformer[A].International Symposium on PIMMRC[C]. Athens, Greece, 2007. 1-5.

[9] HO W W L, LIANG Y C. Optimal resource allocation for multiuser MIMO-OFDM systems with user rate constraints[J]. IEEE Transactions on Vehicular Technology, 2009, 58(3):1190-1203.

[10] ZHANG Y J, LETAIEF K B. An eff i cient resource-allocation scheme for spatial multiuser access in MIMO-OFDM systems[J]. IEEE Transactions on Communications, 2005, 53(1):107-116.

[11] SHEN Z K, CHEN R H, ANDREWS J G, etal. Low complexity user selection algorithms for multiuser MIMO systems with block diagonalization[J]. IEEE Transactions on Signal Processing, 2006, 54(9):3658-3663.

[12] KIVANC D, LI G Q, LIU H. Computationally efficient bandwidth allocation and power control for OFDMA[J]. IEEE Transactions on Wireless Communications, 2003, 2(6):1150-1158.

[13] 张健, 刘元安, 谢刚等. 低复杂度的多用户MIMO下行链路块对角化算法[J]. 电子科技大学学报,2011, 40(5):662-666.ZHANG J, LIU Y A, XIE G, etal. Low complexity block diagonalization algorithm for multiuser MIMO downlink systems[J]. Journal of University of Electronic Science and Technology of China, 2011,40(5):662-666.