基于前缀区间集合的IPv6路由查找算法

崔宇，田志宏，张宏莉，方滨兴

(哈尔滨工业大学 网络与信息安全技术研究中心，黑龙江 哈尔滨 150001)

1 引言

近年来，IPv4地址日渐枯竭，IPv6普及过程逐步加快，IPv6相关技术和服务支持得到了快速的发展，导致 IPv6分配的地址范围和网络流量迅猛增加，因此需要更加高效的IPv6路由算法为数据分组的快速转发提供支撑。

与IPv4相同，IPv6路由方式也为最长前缀匹配，因此可继承IPv4的部分路由算法，但在算法性能方面，两者有以下区别：1) IPv6地址长度128 bit，IPv4为32 bit，使得按位比较的相关算法（如Binary Trie、Multi-bit）的查找树深度增大，造成最坏时间、空间复杂度大量增加；2) IPv4路由规模基本稳定而IPv6处于发展阶段，路由条数始终保持增长趋势，根据文献[1]对BGP路由表的统计，路由条数从2004年的500条增加到当前约8 000条，规模和分布存在较大不确定性，这对以前缀分布特点为基础的相关算法影响较大，同时，由于更新相对频繁，以前缀值为基础的相关算法形成的查找树中不平衡现象会加强，影响查找和更新效率；3) IPv4和 IPv6前缀长度体现了一定的集中性，目前，IPv6前缀绝大部分为32和48，而文献[2]也预测未来前缀长度集中在32、47、48和64，这与IPv4分布相异，导致长度分布敏感的算法性能下降；4) IPv6前缀分布较为集中，从文献[1]的数据可知，高16 bit为0x2001的前缀占30.5%，分布极大不平衡，这对前缀位敏感的算法不利，比如若干集中分布的前缀会出现在Patricia[3]树的同一子树下，增加局部查找深度，这主要是前期地址分配不平衡和地域发展不均匀所致，而随着IPv6的普及，不平衡现象将会减少。

上述分析表明，目前，IPv6前缀存在分布集中和更新频繁2个主要特点，因此良好的IPv6路由算法不仅在理论上应具有较好的平均时间和空间复杂度，还应在集中或稀疏区域具有较好的局部性能，同时也适应路由前缀更新频繁的特点。目前，IPv6使用的软路由算法可分为2类：其一是以IPv4为基础的通用型算法；其二是针对IPv6特点实现的特定型路由算法。

以 IPv4为基础的通用型算法主要分为基于前缀位、前缀长度和前缀值3种。

基于前缀位的路由查找算法主要以二进制树（binary trie）为基础，具有O(W)相关的查找与更新复杂度（W为地址长度）。该方法存在3个问题，其一是树中存在大量不包含前缀的空节点，浪费大量内存；其二是空节点的存在增加了大量无用的比较次数；其三是可能导致已经找到最长匹配前缀却继续向叶子节点查找的情况，增加无效比较的次数。为了去除树中空节点，Patricia方法对二进制树中的连续空节点进行了压缩，解决了前2个问题。文献[4]中的多分枝Trie树(multibits trie)通过将kbit整合到一个节点中，实现了O(W/k)的查找复杂度，降低了查找树的深度。文献[5]提出的优先树(priority trie)对二进制树结构进行了翻转，可优先处理长度较长的前缀，同时去掉了树中的空节点，部分解决了二进制树的 3个问题，查找和更新时间复杂度介于[O(logN),O(W)]之间（N为路由数目），是近些年出现的较新颖的算法。

Waldvogel在文献[6]中提出了基于前缀长度的二分查找方法。该方法具有O(logW)的查找复杂度，但需要大量的初始化计算和复杂的更新过程，同时也会产生大量的Marker，增加计算复杂度和内存空间。文献[7]通过复杂算法降低了Marker数量，进而降低整个算法的内存占用。该类方法以散列为基础，必然会产生散列冲突，影响算法效率和实际效果。

基于值的路由策略主要有二分查找树(BST)和按前缀范围进行二分查找(BSR)2种。在BST中，前缀按值顺序排列，递归选取子序列的中间位置进行比较，直到子序列前缀数为1停止，查找的时间复杂度为O(logN)。BST方法不存在空节点，因此最大程度地节省了空间，具有O(N)的空间复杂度。但BST方法因前缀层次问题，在构建时会出现不平衡现象，增加了查找深度。文献[8]提出的 DPT算法通过对前缀进行 leaf-pushing扩展形成了平衡二叉树，从而避免不平衡现象。文献[9]以最内层节点为树节点，同时用数组维护前缀的包含关系，提出了只使用不相交前缀进行二分查找的方法，避免初始条件下不平衡的发生。

BSR[10]方式用[s,f]表示一个前缀，其中，s表示前缀起始值，补0扩展，f表示结束值，补1扩展，两者差值表示前缀的范围。BSR将点集进行排序，形成有序点集{s1,f1,s2,s3,f3,f2,…}并对其进行初始化计算以存储每个节点对应的最优前缀(BMP,best match prefix)，对其进行二分查找，时间复杂度为O(log2N)。BSR算法由于用2个点表示前缀，因此最多需要前缀数量二倍的节点。同时，由于需要序列进行重新计算，因此更新的时间复杂度最坏为O(2N)。为了提高该方法的更新复杂度，文献[11]提出了Multi-Range-Tree方法将查找和更新的时间复杂度提高到O(logk2N)，但存在频繁更新导致不平衡的可能，同时空间复杂度增加到了O(kNlogk2N)。文献[12]也提出了查找和更新复杂度为O(logN)的算法，通过维护N+1棵树来维护前缀间、前缀与前缀间隔的包含关系，实现快速地更新，但实现难度较大。与文献[11]类似，两者的核心均是保存前缀的包含关系。文献[13]提出的RBMRTs方法将前缀进行分层，不被其他前缀包含的前缀是第一层前缀，只包含于某个第一层前缀A的前缀形成A的第二层前缀，以此类推。同层前缀之间不存在包含关系，因此可以减少更新时的计算量，实现了约为O(log2N)的查找和更新复杂度。

针对 IPv6特点实现的特定路由算法通过对路由表分布特性的分析，利用各种通用算法的特点，将多种通用算法组合成新算法。如文献[14]提出的TSB方法就是将二叉树、段表和路由桶技术结合的IPv6路由算法。其利用IPv6前缀分布特点形成的第一层二叉树结构，只需要较少节点，同时结合段表和桶路由技术，可较好地提高算法性能并降低内存占用。该算法第二层路由桶和段表结构切换时需要进行数据结构的整体切换，会产生一定延时。TSB是多种算法组合，会在特定局部含有某算法的缺陷，但整体上，TSB组合各算法的优点降低单一算法在特定条件下的缺点。随着 IPv6发展，TSB第一层二叉树节点数目会不断增加，降低查找性能，但这种增加不会在短时间内频繁进行。

由于IPv6地址长度较大，且分布集中，因此理论上基于前缀值的具有O(logN)时间复杂度的相关路由算法比O(W)相关的前缀位算法有更好的性能。所以，本文对BSR相关路由算法进行了研究，分析其查找和更新过程中存在的问题，结合IPv6前缀特点，提出了结合段表和 BSR 2种通用算法并以RBMRTs为基础的基于前缀区间集合的IPv6路由算法BSRPS (binary search on range of prefix set)。

2 前缀值相关算法中查询与更新的不平衡性

BSR相关路由算法在IPv4中具有较好的性能，但在IPv6环境中存在的前缀分布与更新不平衡性会严重影响该类方法的性能。本节对该类算法存在的2种不平衡性进行举例和理论分析，指出其在IPv6环境中存在的严重问题，提出了解决该问题的基本思路。

2.1 查询不平衡性

BSR中，前缀按值排序形成{s1,f1,s2,f2,…,sm,fm}前缀值序列（假设不存在包含关系），查找时通过二分查找确定位置，进而与某一路由条目进行对应。表1为一前缀实例，地址长度为5(W=5)，前缀P1～P7集中分布于地址空间[2, 15]上，P8相对孤立。以这种前缀集合形成的BSR和Patricia的基本形式如图1和图2所示。

表1 前缀实例

可以看到，BSR方法中，集中区域的前缀具有较浅的深度，而 Patricia相反，集中区域的前缀深度较大。如前缀P5，在前者中深度为3，后者为5。反之，对于处于稀疏区域的前缀，如P8，BSR中深度为4，而Patricia中为2，差别较大。

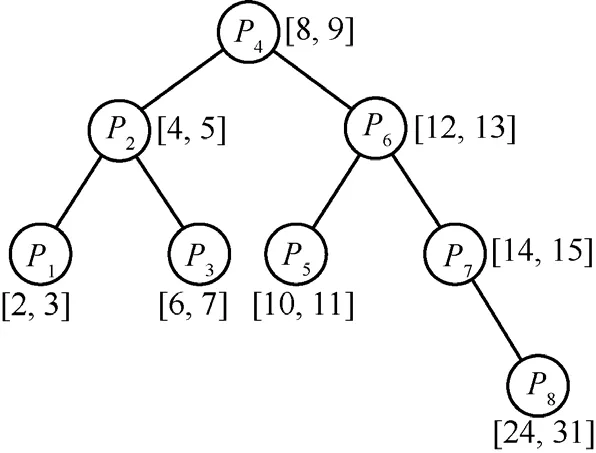
图1 BSR查找树

图2 Patricia查找树

理论上，考虑一种极限情况，假设在某一集中区域中存在拥有共同前缀a的2m-1个连续等长前缀，其范围为{[a×2m +0,a×2m +1], [a×2m +2,a×2m +3],…, [a×2m+2m-2,a×2m +2m-1]}，以及1个前缀为b(b!=a且与a等长)的前缀Px。则在 BSR中，Px必然处于查找树的最左端或最右端，因此其查找深度为log(1+2m-1)，约为m-1；而在Patricia中由于b!=a，Px的查找深度为2。对于连续的2m-1个前缀，查找深度分别为m-1和1+m，差别较小。可见，基于前缀区间的相关查找算法对集中区域的前缀有较好的查找性能，而基于前缀位的相关算法(如 Patricia、Multi-bit)对稀疏区域前缀的查找性能较好。

不同于IPv4，IPv6前缀分布的不均匀会严重增加 BSR算法的不平衡性。首先，目前的 IPv6中含有大量0x2001起始的前缀，分布集中，这对稀疏区域前缀的查找影响较大；其次，稀疏区域中存在的一些特殊前缀，如2002：：/16（6to4隧道）约占整体流量40%，会严重影响路由的整体性能。因此，为了避免这种情况，本文通过结合前缀位路由算法的思想，对前缀进行一次范围划分以减轻稀疏区域前缀查询的不平衡性，将在第3节中详细介绍。

2.2 更新不平衡性

BSR相关路由算法在不断更新后可能会产生极端不平衡情况，比如图1中删除前缀P8[24, 31]并逐次插入P8[16, 17]、P9[18, 19]、…、P15[30, 31]后形成的查找树如图3所示。

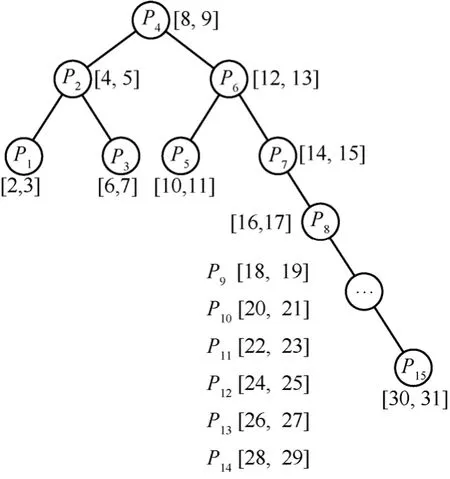
图3 更新不平衡性举例

从图3可见，按照BSR基本更新方法插入前缀P8～P15会产生众多单分支节点。若不进行平衡旋转，则必然会增加查找深度。在最坏情况下，整个查找树会出现每个节点均为单分支的情况，查询时间复杂度降为O(N)。

由于IPv6前缀更新较为频繁，因此查找树的形态会对BSR的查询效率产生极大影响，必须有效控制最坏情况的出现，降低其对查询效率产生的影响。为此，本文借鉴了Muliti-bit方法中对若干前缀位进行合并的思想，将前缀区间进行第二次划分，形成前缀区间集合，达到有效地降低查找树深度的目的。并且，在更新后配合节点自修复算法以避免大量空置集合的出现，降低内存占用量。

3 基于前缀区间集合的IPv6路由查找算法

BSRPS算法以RBMRTs为基础，针对IPv6前缀长度、分布范围等特点，通过地址范围划分和前缀集合划分对 RBMRTs基础结构进行改造，构造BSRPS树，进行查找与更新。更新时，对更新过程中涉及到的节点使用自修复算法以避免前缀集合划分引入的空位，降低不断更新对查找树平衡性的影响。本节首先介绍 BSRPS算法经二次划分后形成的多棵多层查找树的结构，其次分别介绍查找和更新算法。

3.1 BSRPS算法划分方法与框架

BSRPS以RBMRTs为基础，后者将前缀进行分层，形成单棵、多层二分查找树。图4显示了表1和表2所示前缀形成的查找树。

表2 前缀补充实例

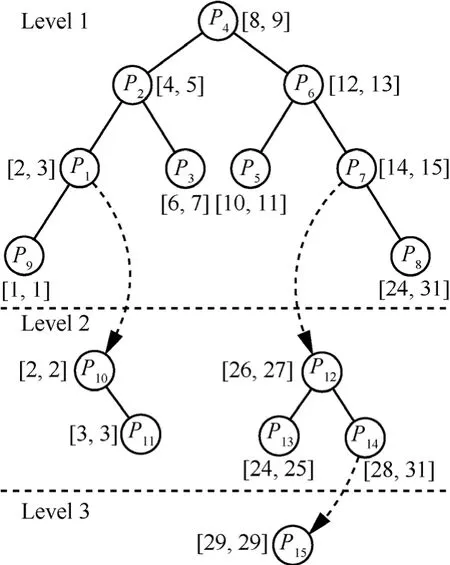
图4 RBMRTs算法框架

图4中，RBMRTs将前缀集合分成若干层，同层前缀不存在包含关系，层间前缀为包含关系，称包含于某一前缀的若干前缀形成的树为该前缀的包含子树，如P10、P11形成了P1的包含子树。该结构有以下2点优势：1) 同层无包含关系可省去BSR中一部分预计算和更新时间；2) 查询和更新算法也相对简单。查询时，首先在Level1中进行查询，如果不存在则返回空，若前缀节点存在包含子树则进入下一层查询，否则返回该前缀。更新过程与查询类似，但增加了层间移动、替换等操作。

BSRPS设计中，首先用地址范围划分将Level1进行分割，形成多棵第一层树，如图4中若按地址范围四等分可形成{P9,P1,P2,P3}、{P4,P5,P6,P7}和{P8} 3棵第一层查找树。之后将每棵查找树的若干节点组合为一个众节点，形成BSRPS查找树。

3.1.1 地址范围划分

RBMRTs算法基于BSR，因此对集中区域前缀的查询能力较好。为了提高稀疏区域前缀性能，需通过地址范围划分分离稀疏区的IPv6前缀，避免其查询时间被平均化，提高对稀疏区前缀的查询效率。为此，本文采用对地址空间进行分段的方法，将地址空间分成K段，占用地址的高logKbit，形成多棵第一层树。

对于K的选择有以下考虑：1) 空置率，在前缀覆盖范围一定的情况下，K增大，每段范围缩小，空置率可能会增加，内存浪费增大；2) 分散率，K越大，第一层树越多，分散越广，查找性能越高；3) 被覆盖率，若K很大，logK也会增大，假设存在某个前缀Px，其长度Lx小于LogK，那么则要进行位扩展到logKbit，从而增加2Lx-logK个前缀，内存占用增加，也增加了更新的复杂度。良好的路由算法应具有低空置率、高分散率和零被覆盖率。对于 IPv6，目前最短前缀长度为 16，除去最高 3 bit的全局地址标识，可以用高13位分段，K=213，既可以避免被覆盖现象，又可以最大程度上划分子树，分散率最高。

根据这种划分，Potaroo路由表最终形成了如表3所示的前缀分布情况。其中，Num表示经划分后，查找树中节点数目为[1, 10]、[11,100]、[101, 1 000]或[1 001, ∞]的查找树类型；Count.表示该类型查找树的数目，比如节点个数在[101, 1 000]范围内的查找树有17棵；Percent表示该类查找树包含的前缀占前缀总数的百分比，可以看出100+类型包含了最多的前缀；Acc-Rate表示极限情况下各个段中查找深度在划分前后的理论比值，体现了极限情况下查找的加速情况。

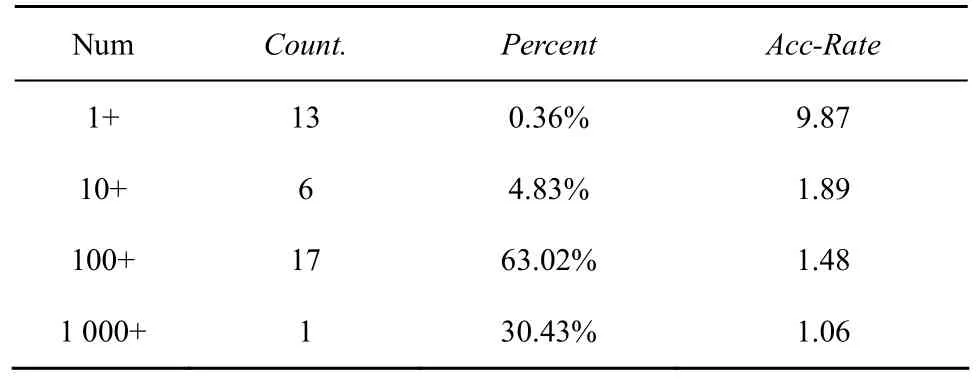
表3 前缀分布关系

可以看到，100+类型的前缀占整体数目的63.02%，且理论上可加速到 1.48倍，因此这种分段方法可有效提升整体的性能。同时，根据笔者对IPv6网络中骨干路由器统计，稀疏区域 1+类型包含的以“2002：：”开头的前缀(6to4隧道)占有了约 40%的流量，经过地址范围划分，该类流量理论上可提升到9.87倍，提升效果明显。可见，对地址范围的有效分段可以较大提高 IPv6路由转发的性能，是十分必要和有效的。

3.1.2 前缀集合划分

前缀集合划分借鉴了 Multi-bits前缀位集合方法，在前缀按值升序排序基础上，将M个连续前缀划分为一个前缀集合，称为众节点，并用[Ss,Se]表示该众节点的范围。假设图4所示前缀经地址划分后属于同一查找树，图5则表示经过集合划分（假设M=3）后的情况。

图5 集合划分框架

前缀集合划分直观上反映出3个特点：1) 每个众节点含有多个前缀；2) 查找树深度降低；3) 众节点存在空闲位置。查找树深度降低是前缀合并的必然结果。原始情况下查找树深度为logN，集合划分后，查找树深度变为 log(N/M)，总层数减少了logM。这对于查找失败选择默认路由的情况是有利的，可减少logM次比较。

众节点会存在空闲位置，如Level3中P15所在众节点，其根本原因是原始情况下查找树包含的前缀数不能被M整除，因此必然在查找树最右众节点出现空闲现象。由于空闲情况只在最右出现，且目前路由表不会形成大量的包含子树，因此不会产生浪费大量内存的情况。而在更新过程中，插入和删除可能会形成空闲位置，需要对更新节点进行自修复以避免不断更新产生大量的空闲众节点，将在3.3节详细说明。

3.2 BSRPS查找

从图5可知，BSRPS虽然形成了众节点，但查找树基本框架未变，因此可根据每个众节点的范围进行二分查找。算法首先需要定位到某一众节点，假设Ni表示某棵查找树，则定位某一众节点的时间复杂度为 log(2Ni/M)。之后仍用二分查找定位该众节点中的前缀，时间复杂度为logM。单棵查找树总时间复杂度为log(2Ni/M)+ logM=log2Ni，与原始算法一致。因此，对于单棵查找树，BSRPS并没有提升理论上的查询复杂度，主要是降低更新不平衡对查找性能的影响，但对于查找失败进行默认路由的情况，查询复杂度降为 log(2Ni/M)，性能有一定提升。在加入地址范围划分后，平均时间复杂度有所降低，为 log(2Ni/K)。下面给出查找算法，其中，bs-set(pt,address)对一个众节点中的M个前缀进行二分查找，Prefix-set表示第一层查找树。

算法1BSRPS主查找算法

算法2子树内递归查找算法

3.3 更新与自修复

BSRPS的更新过程与RBMRTs类似，包括同层内添加删除前缀和层间前缀子树的替换与扩展。但是，由于 BSRPS采用了众节点模式，在比较和移动时略有不同，如图6显示了添加前缀Pnew时的3类情况（删除过程类似）：1) 添加的前缀只与一个众节点相关，如图 6(a)～图 6(d)所示；2) 与任何众节点均无关，如图6(e)所示；3) 与多个众节点相关，如图6(f)所示。

图 6(a)中，Pnew覆盖了整个众节点，用只包含Pnew的新众节点进行替换，同时将包含P1～Pm的原始众节点扩展为Pnew包含子树；图6(b)表示Pnew包含了原始众节点的部分前缀，此时将P2、P3形成新的众节点并扩展为Pnew的包含子树，并用Pnew替换两者原始位置；图6(c)中，Pnew属于P3的子前缀，进入P3的包含子树更新；图6(d)表示Pnew位于该众节点中两个连续前缀中间，此时需要挪动众节点中的其他前缀以重新形成有序数列。若该众节点是满节点，则在插入Pnew时必须要移出P1或Pm，此时P1或Pm需以该众节为根节点进行如图6(e)的插入过程，否则挪动单侧前缀即可形成新有序数列；图6(e)表示Pnew不包含于任何众节点，若PresetB未满，则填入PresetB末尾，否则新建一众节点并链到PresetB的右孩子处。反之亦然。

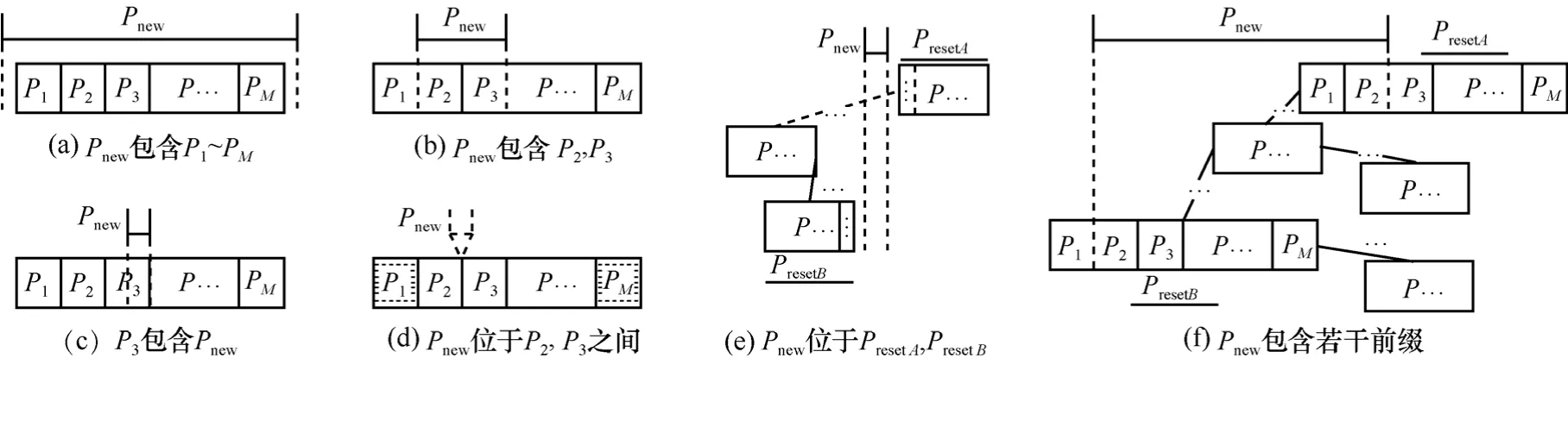
图6 BSRPS更新情况（Preset表示众节点）

当Pnew涉及多个众节点时，更新操作相对复杂，如图6(f)显示了向左子树扩展多个众节点的情况。可以看到Pnew覆盖了PresetA的前面部分、PresetB的后面部分，且对于所有大于PresetB.P1小于PresetA.P3的前缀（斜杠条纹显示），这些需要被替换的众节点组成Pnew的包含子树（与RBMRTs相同，需要对包含子树进行平衡旋转，防止出现大量单分支众节点）。而Pnew则被加入PresetA或PresetB，更新原有众节点。

上述方法可正确更新，但存在以下2个问题：1) 缺少机制保证被更新的众节点是满的，这会导致该众节点可能只剩下极少的有效前缀，如图6(a)、图6(f)分别会使一个和2个众节点包含的前缀数目大量减少，众节点的空置率偏高，浪费大量内存；2) 当出现大量不满众节点时，必然会增加查找树的深度，影响查询和更新效率。为此，本文提出了更新节点的自修复算法以避免出现上述情况，保证最坏的查询复杂度为log(2N/KM)。

节点自修复算法的核心思想是当众节点自身在更新后不满时，不断从小于或大于该众节点的区域中取最接近前缀以填补该众节点的空白，直到该众节点满。该算法主要包括4个操作：重排序、定位、移动和旋转。下面以图7为例说明这一过程。

图7 自修复算法举例

图7(a)中假设PresetA中前缀P2被替代或被删除后，PresetA进入自修复过程（更新过程涉及的所有众节点均需进行自修复，以保证除叶子节点外的所有众节点均为满众节点）。首先假设PresetA优先选择从左子树取最接近的前缀，则PresetA需要对自身进行重排序留前部的空位，如图7(a)所示；之后查找左孩子的最右子树以定位小于该众节点的最近前缀，如图7(b)所示，将P12挪动到PresetA的空闲处。此时，PresetD虽被更新但由于其为叶子节点因此不需要进行自修复。图6(c)假设PresetB的右子树PresetD中的前缀已经全被修复到PresetA的第一个位置上，因而必须从PresetB的末尾选择前缀移动到PresetA的前部。由于PresetB不是叶子节点（含有左子树），因此也要执行自修复。此时，PresetB有2个可用策略：1) 从其左子树里不断移动最接近的前缀补位；2) 若其左孩子非叶子节点，则可首先进行旋转，再移动P6到PresetA中，如图7(c)的右侧部分，既可以降低更新的时间复杂度，还可平衡查找树，降低查找深度。

前缀集合划分和更新节点的自修复并不能避免不平衡性的出现，但可以减少最坏情况下查找和更新的复杂度。同时，在配合使用AVL算法时，查找树节点总数从N降为N/M，可节省大量平衡开销。

4 性能分析与实验

本节通过理论分析和实际测试对 BSRPS算法的性能进行了评估。首先在内存使用上，该算法首先进行了区域划分，将 Level1层查找树分成了K份，因此需要O(K)的空间存储树根指针；同时，由于一般情况下只有最右众节点可能存在不满情况，因此空间复杂度为O(K+2N)。但在经过不断更新后，由于叶子节点无法进行自我修复，会出现叶子众节点中只含有极少前缀的情况，浪费存储空间。在这种情况下，对于二叉树而言，假设其含有的非叶子众节点个数为x，那么叶子众节点数目至多x+1，由于Mx+1×(x+1)=2N，可推导出x=(2N-1)/(M+1)，由此查找树占用的内存为M×(2x+1)≈2M(2N-1)/(M+1)，因此算法最坏空间复杂度为O(K+4N)。

在时间复杂度上，对于每一层查找树而言，该算法拥有log2Ni的查询速度。但是，前缀中存在若干包含子树，实际查询效率必然会低于该值，且查询效率随层数增多而下降。目前前缀最多包含5层，且每层的个数不定，不利于理论分析，因此通过实验进一步分析其对查找性能的影响。在更新方面，与查询过程相同，首先定位新前缀位置，进而向下替换或者更新，其最多需要对2个众节点进行自修复（如图 6(f)所示情况），因此更新复杂度为O(log2Ni+2M)。

为了测试算法实际性能，笔者在一台2.6 GHz主频、16 GB内存的服务器上对该算法进行了对比测试。对比算法采用 Patricia、BSR和 RBMRTs 3种，实验数据采用了文献[1,15]提供的 Potaroo、Tokyo和Atlanta路由表。表4列出了3个BGP路由表的相关参数。

表4 3种路由表及内存占用

表4第2列显示了Potaroo、Tokyo和Atlanta 3个路由表中路由条数，均在8 000左右。第3～6列显示了4种路由算法在不同路由表下的内存占用量，其中，BSR在理论上不存在内存的浪费因此在实际中的占用量也最少，而BSRPS方法理论上的空间复杂度大于 RBMRTs，但实际中却相反，这主要是由于BSRPS方法中，众节点对若干前缀进行了集合，因此对于一个M个前缀的众节点只需2个指针指向左右子树，而RBMRTs方法则需要2M个指针，增加了大量的内存。表4还显示了各个路由表中最深层均为5层、且大部分前缀处于Level1层，因此不会对算法总体性能产生巨大影响。最后一列SEG表示（按照K=8 192计算）地址划分将路由表分成了约28个段（即分成28棵第一层树），分配较不平均，有效分段只占3.4%。随着IPv6的发展，当高16 bit地址使用明显增加时，有效分段比例也会有明显提高。

为了测试算法的查询和更新速度，本文选择M=5，K=8 192。理论上，M大小不影响查找速度，但M较大时会影响算法的内存占用量。同时，M的大小也与算法的更新时间复杂度相关，在当前路由条数在 8 000左右的情况下，logN约为 13，选择M=5可不过分突出众节点重排序的时间开销。在以上条件下，表5显示了4种路由算法在查找Potaroo路由表时，不同分布前缀的查询能力。其中，1 000+表示地址范围划分后前缀个数大于1 000的查找树（与表 3相同），表中数值表示该算法对于该类查找树各层部分前缀的平均查找时间。

表5中，Patricia对集中区和稀疏区前缀的查询速度有较大差异，稀疏区的查询速度明显优于集中区，差距在4倍以上。BSR基本保持平均，对集中区的查询速度优于Patricia，而稀疏区慢于前者。RBMRTs方法与BSR方法类似，性能相差不多。BSRPS算法由于进行了地址划分，生成了多棵Level1层查找树因此与Patricia具有相似的性能趋势，均对稀疏区域的前缀有较好的查询性能。而与BSR和RBMRTs相比，在集中区，BSRPS与前两者性能相近，这是由于集中区形成的Level1层查找树中节点总数并没有成指数级的降低，查找树深度降低不明显，从而导致性能提升不高。在稀疏区，由于 BSRPS地址范围划分使得稀疏区前缀形成的独立查找树只具有少量的节点，查找深度大量减少，因此性能有很大提高。Tokyo和Atlanta路由表的测试结果与Potaroo类似。

在更新测试中，本文针对 Potaroo前缀集合首先对图6所示的6种情况进行了更新测试。测试选取集中区域（1 000+，D）和稀疏区域（10+，F）的若干第一层子树节点进行了插入测试。

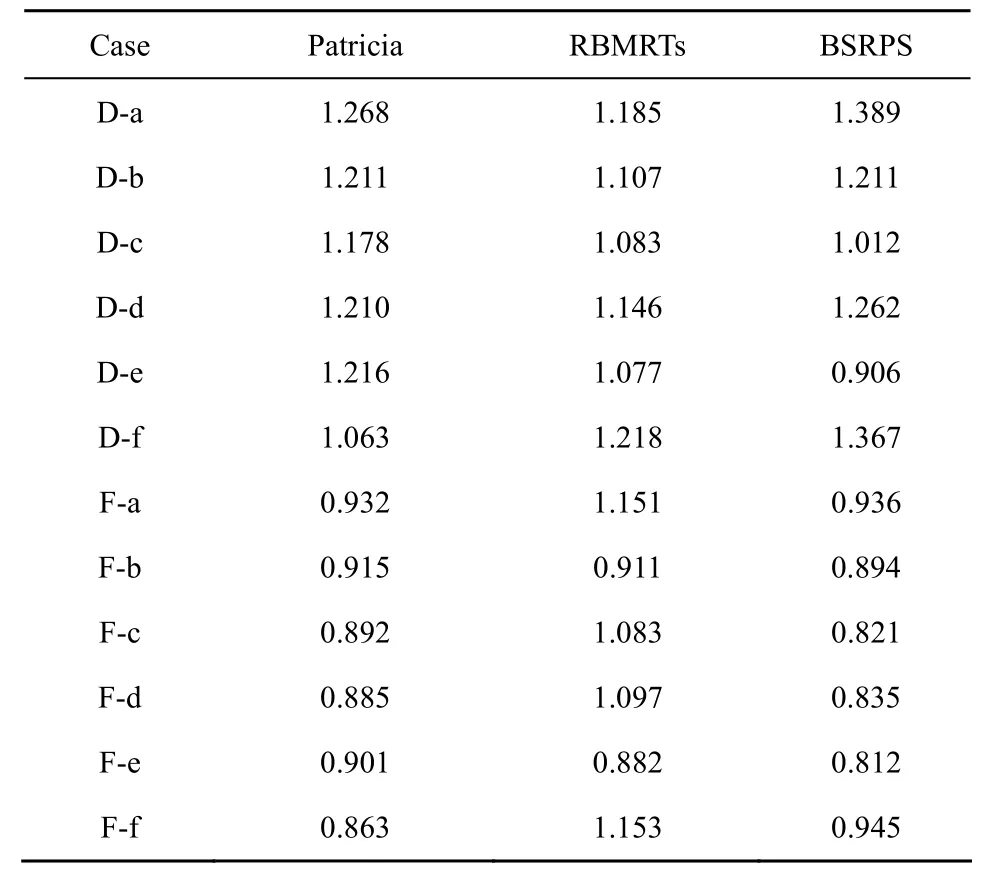
表6 Potaroo更新性能/μs

表6中，BSRPS方法在稀疏区域（F）的更新性能与 Patricia相当，且由于查找性能提高和较少的自修复过程，整体更新性能优于RBMRTs算法。在集中区域（D），c/e 2种更新情况不需要复杂的更新流程，时间少于RBMRTs；在a/b/d/f 4种情况下，由于需要建立子树或更新节点自修复等相对复杂的更新流程，BSRPS算法较RBMRTs增加了至多20%的更新时间。其中，a/b/f 3种情况表示Pnew前缀包含多个原有路由前缀的情况，d情况表示Pnew前缀处于原有2个前缀之间。通常路由更新时并不能进行查找操作，因此当上述4种情况频率较高时，会增加分组丢失概率，降低用户体验。相反，若更新的情况主要是c/e 2种情况，如在新启用的地址空间中分配 IPv6的前缀时，更新性能相比RBMRTs会有所提高。

为了验证 BSRPS在极端情况下的性能，本文针对集中区（Du）与稀疏区（Fu）子树第一层进行了连续插入 64个递增前缀的极端环境测试，并获得了这种情况对于查找速度的影响（Du-L，Fu-L），测试结果如表7所示。可以看到，BSRPS算法更新时间较长，但不超过RBMRTs的115%。在经过极端插入后，BSRPS算法在集中区和稀疏区均具有较好的查询速度，查询时间仅为 RBMRTs的 30%左右，Patricia的 40%左右。主要原因是连续插入的64个递增前缀会在RBMRTs查找树下形成深度为64的局部单链子树，BSRPS形成深度为64/M的局部单链子树，查找性能有线性级的提高。理论上，Patricia深度增加最少，为对数级。

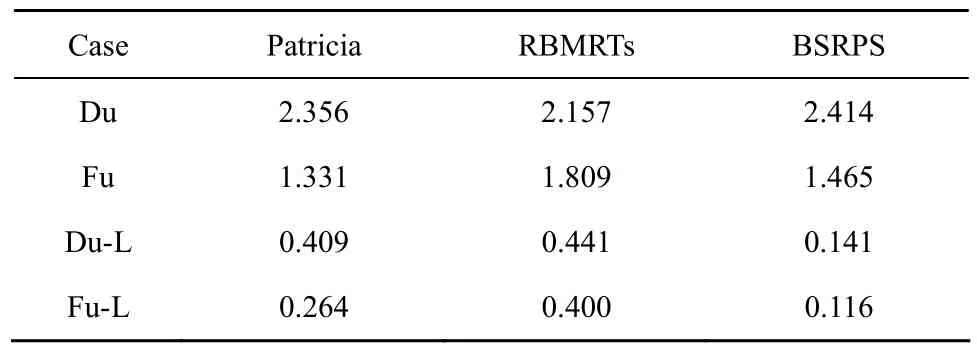
表7 Potaroo极限情况/μs

5 结束语

高效的 IPv6路由算法是提高网络传输性能的重要因素。本文提出的BSRPS算法通过地址范围划分、连续前缀集合和更新节点自修复算法在牺牲一定更新时间的条件下有效地提升了平均和极端情况下的查询速度，同时也降低了内存的占用量，具有较好的性能。测试结果表明，查找性能在平均情况下性能比RBMRTs提升1.5倍，极端情况下提升3倍以上。

本文的研究仍存在一定不足。首先，M取值没有给出规范的公式，这需要与内存和更新时间联合评估；其次，本算法未从根本上消除RBMRTs算法频繁更新产生的不平衡性，只是降低不平衡性对查询的影响。当使用AVL进行平衡时，由于降低了节点总数，因此可提高AVL的性能；再次，集中区域a/b/d/f 4种情况下更新时间有所降低，增加更新过程导致分组丢失的概率，需进一步研究；最后，地址划分的有效性较低，有效值仅为 3%，对集中区域的性能提升效果不佳，可采用文献[14]中将2001：：/16前缀进行单独划分等方式进一步优化。

[1] http：//bgp.potaroo.net[EB/OL].2010.

[2] SUN Q, HUANG X H, ZHOU X J.A dynamic binary hash scheme for IPv6 lookup[A].Proceedings of IEEE GLOBECOM[C].New Orleans,USA, 2008.1-5.

[3] RUIZ-SANCHEX M A, BIERSACK E W, DABBOUS W.Survey and taxonomy of IP address lookup algorithms[J].IEEE Network, 2001,15(2)：8-23.

[4] SAHNI S, KIM K S.Efficient construction of multibit tries for IP address lookup[J].IEEE/ACM Trans Networking, 2003, 11(4)： 650-662.

[5] LIM H, YIM C H.SWARTZLANDER E.Priority tries for IP address lookup[J].IEEE Transactions on Computers, 2010, 6(59)： 784-794.

[6] WALDVOGEL M, VARGHESE G, TURNER J.Scalable high speed IP routing lookups[A].Proceeding of ACM SIGCOMM[C].Cannes,France, 1997.25-36.

[7] Kim K S, SAHNI S.IP lookup by binary search on prefix length[A].ISCC '03 Proceedings, of the Eighth IEEE International Symposium on Computers and Communications[C].Antalya, Turkey, 2003.77-82.

[8] LIM H, KIM W, LEE B.Binary search in a balanced tree for IP address lookup[A].IEEE Workshop High Performance Switching and Routing[C].HongKong, China, 2005.490-494.

[9] LIM H, KIM H, YIM C.IP address lookup for internet routers using balanced binary search with prefix vector[J].IEEE Transactions on Communication, 2009, 57(3)：618-821.

[10] LAMPSON B, SRINIVASAN V, VARGHESE G.IP lookups using multiway and multicolumn search[J].IEEE/ACM Trans Networking,1999, 7(3)：324-334.

[11] WARKHEDE P, SURI S, VARGHESE G.Multiway range trees： scalable IP lookup with fast updates[J].Computer Networks, 2004, 44： 289-303.

[12] SAHNI S, KIM K S.AnO(logN) dynamic router-table design[J].IEEE Transactions on Computers, 2004, 53(3)：351-363.

[13] ZHONG P F.An IPv6 address lookup algorithm based on recursive balanced multi-way range trees with efficient search and update[A].Computer Science and Service System (CSSS)[C].Paris, France, 2011.2059-2063.

[14] 李振强, 郑东去, 马严.TSB：一种多阶段 IPv6 路由表查找算法[J].电子学报, 2007, 35(10)：1859-1864.LI Z Q, ZHENG D Q, MA Y.TSB：a multi-stage algorithm for IPv6 routing table lookup[J].Chinese Journal of Electronics, 2007, 35(10)：1859-1864.

[15] http：//www.routeviews.org[EB/OL].2012.