不同设计参数下刚构－连续组合曲线梁桥地震响应敏感性分析＊

揭志羽，卫星，李亚东，顾颖

(西南交通大学土木工程学院，四川 成都 610031)

随着我国铁路建设的快速发展，施工技术不断完善和铁路建造标准的提高，更多地考虑铁路线形的要求。曲线桥所以现在广泛地用于铁路桥梁中，考虑到各方面的因素，刚构－连续组合梁桥比单一的刚构桥和连续梁桥具有一定的优势。由于刚构－连续组合曲线梁桥的设计参数会对其地震响应产生很大的影响。国内外的学者对此进行了大量的研究［1－12］，但是，对铁路桥梁中的刚构－连续组合曲线梁桥的研究则很少。本文主要研究不同的设计参数如曲线半径、桥墩墩高及墩梁连接方式等对于刚构－连续组合曲线梁桥地震响应的影响，为今后该类型的铁路曲线桥梁的抗震设计提供借鉴。

1 工程背景

某铁路桥主桥采用刚构—连续组合梁，跨径组合(40+6×80+40)m，桥墩编号为7号墩至15号台，7号墩为主桥与简支梁的交界墩。主桥桥墩墩高及墩梁连接情况见表1，9号墩最高，墩高89 m。10号、11号、12号桥墩与主梁固结，形成刚构，主桥支座采用球形支座，主桥总体布置图见图1。该桥桥上线路为圆曲线(第1跨到第5跨，半径600 m)+缓和曲线(第6跨到第7跨一半)+直线(第7跨一半到第8跨)，建成后将是国内曲线半径最小、联数最多、跨度最大的双线铁路桥。梁体采用C55混凝土，所有墩台采用C40混凝土，设计时速100 km/h，设计荷载为双线ZK活载，线路纵坡为－24‰。表1给出了各桥墩与主梁约束方式。

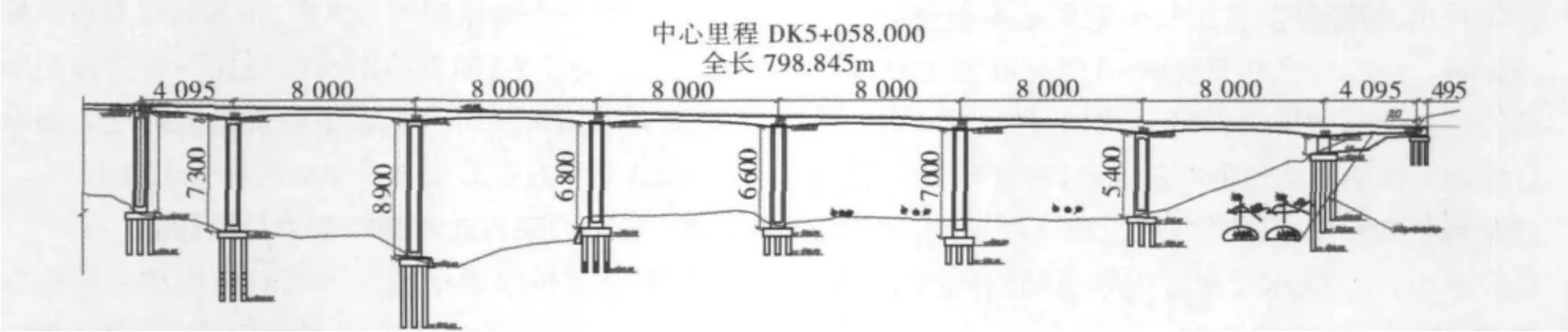
图1 主桥总体布置图Fig.1 The overall arrangement plan of bridg

表1 主桥桥墩墩高及墩梁连接情况Table 1 The height of pier and the connection of pier and girder

2 结构动力特性敏感性分析

利用ANSYS，建立主桥空间有限元分析模型，如图2所示。主梁及桥墩采用梁单元BEAM188模拟。利用质量单元MASS21考虑二期恒载等质量作用。采用弹簧－阻尼单元COMBIN14模拟桩基土刚度。采用门式刚架来模拟桩－土相互作用。

图2 全桥有限元模型Fig.2 FEM model

2.1 曲线半径对动力特性的影响

根据主桥基本设计参数，仅改变上部结构曲线半径，利用ANSYS建立7种不同曲线半径下(∞，1200，1000，800，600，450和 300 m)的桥梁结构空间有限元模型，分析得到结构自振频率及振型。表2给出了部分不同曲线半径下的自振频率和振型。

表2 部分不同曲线半径的自振频率和振型Table 2 The natural vibration frequencies and vibration modes of partial different curve radiuses

动力分析表明，曲线半径大小对桥墩振动特性影响较小，桥墩低阶自振频率数值基本不受曲线半径影响。曲线半径在300 m～1200 m变化时，(1)结构的一阶振型均为纵飘，总体上曲线半径对一阶自振频率影响不大，频率差小于1%;(2)梁体横弯自振频率随着曲线半径的增大而有所增加，但增幅越来越小;(3)梁体竖弯自振频率随着曲线半径的增大而稍有增加。

2.2 墩高对结构动力特性影响

据主桥基本设计参数，通过同时改变所有桥墩高度，利用ANSYS建立5种不同墩高调整量条件下(－20 m，－10 m，0 m，+10 m和+20 m)的桥梁结构空间有限元模型，分析得到结构自振频率及振型。图3所示为部分桥墩纵弯自振频率随墩高调整量的变化曲线。

图3 部分桥墩纵弯自振频率随墩高调整量的变化曲线Fig.3 The natural vibration frequencies of longitudinal flexure of pier with the adjusted quantity of piers height

动力分析表明，墩高调整量在－20～+20 m变化时，结构的一阶振型均为纵飘，桥墩高度对桥墩振动特性影响较大，随着桥墩高度增加纵弯自振频率显著减小;梁体横弯自振频率随着墩高的增大而减小;梁体竖弯自振频率随着墩高的增大而减小。

2.3 墩梁约束方式对结构动力特性影响

为研究桥梁墩梁约束方式对结构动力特性影响，利用ANSYS分别建立7种不同约束方式(见表3)的桥梁空间有限元模型，分析得到结构前10阶自振频率及振型(“1”表示约束，“0”表示不约束，依次表示X(纵向)、Y(横向)、Z(竖向)方向的位移和转角，桥梁的原设计约束是5)。

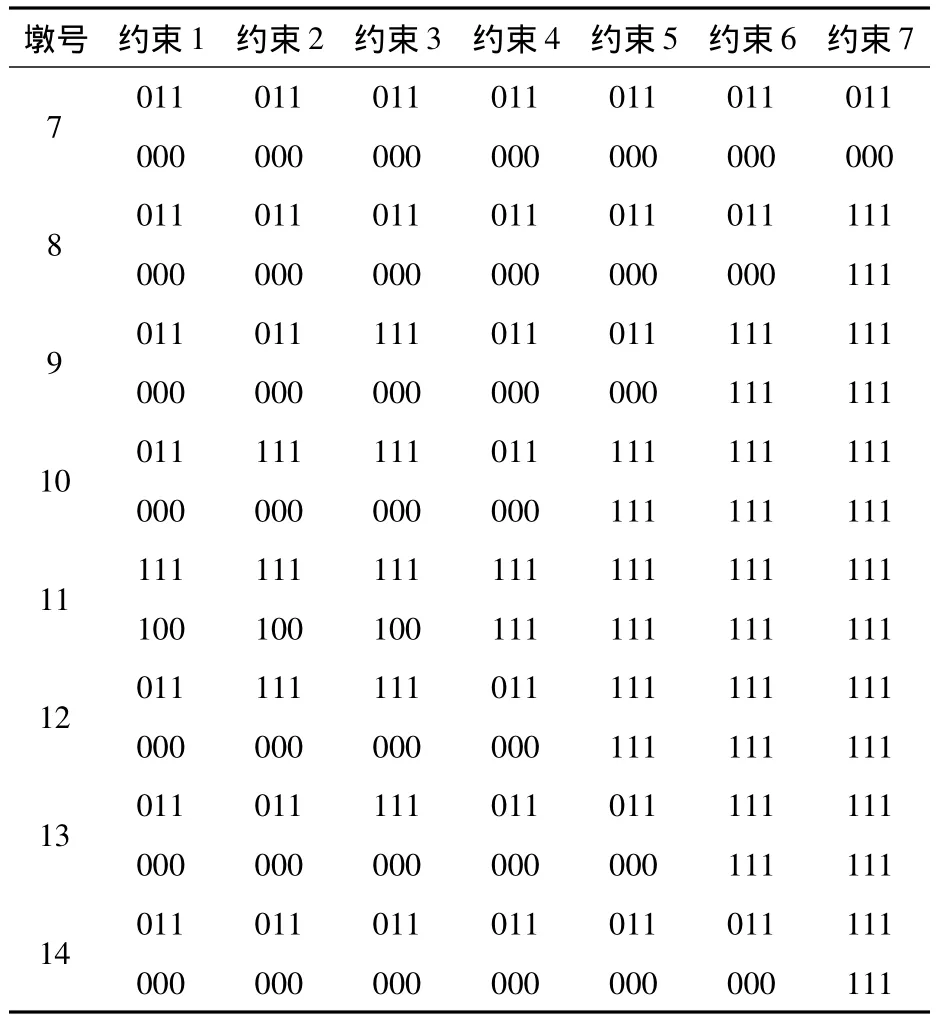
表3 墩梁约束方式Table 3 The constraints of pier and girder

动力分析表明，墩梁连接方式对结构动力特性影响较大:(1)墩梁间的纵向约束对结构纵飘频率影响较大，纵向约束越多纵飘自振频率越大;(2)墩梁间的转角约束对梁体竖弯频率影响较大，转角约束越多竖弯自振频率越大;(3)墩梁约束方式对桥墩自身纵弯频率基本无影响，桥墩纵向受约束后，不出现单独纵弯振型。

3 地震响应对设计参数的敏感性分析

根据《中国地震动区划图》［13］划分，桥址区地震动峰值加速度0.05g，对照地震基本烈度为6度，地震动反应谱特征周期0.35 s。按照《铁路工程抗震设计规范》［14］抗震设防等级为7级，抗震重要性系数Ci为:多遇地震作用下1.5，设计地震作用下1.0，罕遇地震作用下1.0。结构自振周期小于2 s，且阻尼比ξ=0.05时，动力放大系数β由下式决定:

式中:Tg为特征周期，取Tg=0.35 s;A为水平设计加速度反应谱，A=Ciβα;Ci为桥梁重要性系数;α为水平地震基本加速度，取0.05 g。图4所示为水平加速度反应谱曲线。

图4 水平加速度反应谱曲线Fig.4 The response spectrum curve of horizontal acceleration

3.1 不同曲线半径分析结果

根据ANSYS分析结果，图5～8所示为不同曲线半径(300～1200 m)下纵桥向激励下的墩顶、中跨跨中纵向位移及墩底面内弯矩，横桥向激励下的墩顶、中跨跨中横位移及墩底面外弯矩。

图5 纵桥向激励下的纵向位移Fig.5 The longitudinal displacement by the incentive along the bridge

图6 横桥向激励下的横向位移Fig.6 The transverse displacement by the incentive cross the bridge

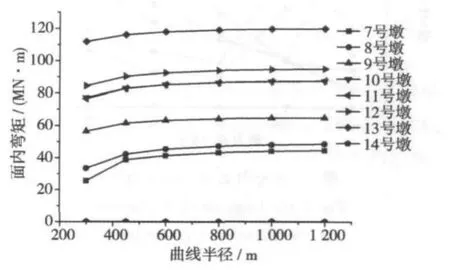
图7 纵桥向激励下的桥墩墩底面内弯矩Fig.7 In－plane moment of the bottom of pier by the incentive along the bridge

纵桥向反应谱作用下，中跨跨中截面的纵向位移随着曲线半径的增加而增加。7号、8号及9号桥墩墩顶纵向位移随着曲线半径的增加而增加，13号及14号桥墩墩顶纵向位移随着曲线半径的增加而有所减小;桥墩墩底截面面内弯矩随着曲线半径的增加有所增大，半径大于600 m之后的增加量很小。

横桥向反应谱作用下，中跨跨中截面的横向位移随着曲线半径的增加先增加后减小，半径超过450m后横向位移变化不大。除8号桥墩外，其他桥墩墩顶横向位移随着曲线半径的增加而增加;除8号、11号桥墩之外的桥墩墩底截面面外弯矩随着曲线半径的增加而增加。

图8 横桥向激励下的桥墩墩底面外弯矩Fig.8 Out－ plane moment of the bottom of pier by the incentive cross the bridge

3.2 不同墩高反应谱分析结果

根据ANSYS分析结果，图9～12给出了不同墩高调整量下纵桥向激励下的墩顶、中跨跨中纵向位移及墩底面内弯矩，横桥向激励下的墩顶、中跨跨中横位移及墩底面外弯矩。

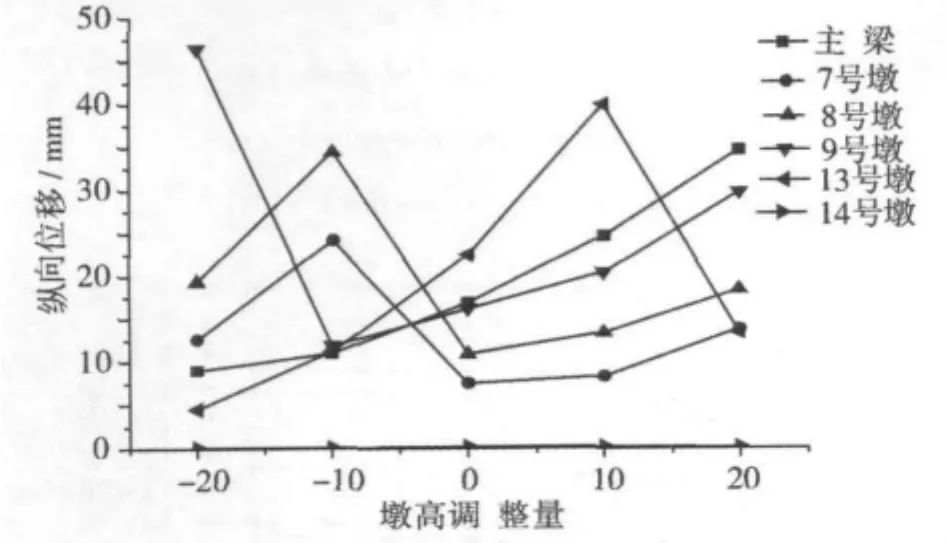
图9 纵桥向激励下的纵向位移Fig.9 The longitudinal displacement by the incentive along the bridge

图10 横桥向激励下的横向位移Fig.10 The transverse displacement by the incentive cross the bridge

图11 纵桥向激励下的桥墩墩底面内弯矩Fig.11 In－plane moment of the bottom of pier by the incentive along the bridge

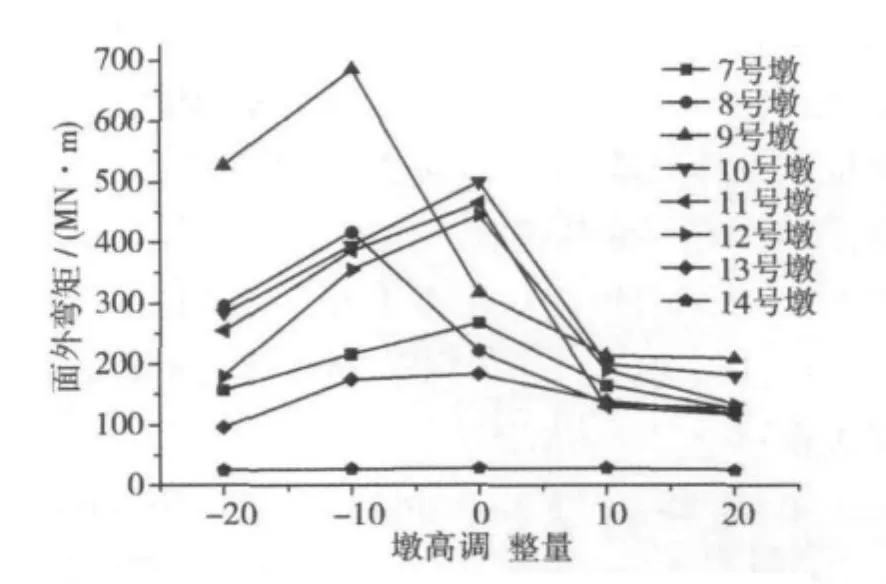
图12 横桥向激励下的桥墩墩底面外弯矩Fig.12 Out－ plane moment of the bottom of pier by the incentive cross the bridge

纵桥向反应谱作用下，中跨跨中截面的纵向位移随着墩高增加有所增加;桥墩墩顶位移和墩底面内弯矩呈非单调性变化，无明显的变化规律。

横桥向反应谱作用下，中跨跨中截面的横向位移随着墩高增加先增加后减小再增加。除了7号桥墩外，其他的桥墩墩顶横向位移随着墩高增加先增加后减小再增加，7号桥墩墩顶横向位移随着墩高增加先增加后减小;7～13号桥墩墩底截面的面外弯矩随着墩高的增加先增大后减小。

3.3 不同约束方式反应谱分析结果

根据ANSYS分析结果，图13～16所示为7种约束方式下纵桥向激励下的墩顶、中跨跨中纵向位移及墩底面内弯矩，横桥向激励下的墩顶、中跨跨中横位移及墩底面外弯矩。

纵向反应谱作用下，中跨跨中截面的纵向位移随着墩梁约束关系的增加与加强先减小后增大再减小。分别在墩梁连接方式等于1和7下，达到最大值和最小值。7号墩墩顶的纵向位移随着墩梁约束方式的增加与加强而减小，8号、9号、13号墩顶纵向位移随着墩梁约束方式的增加与加强而先增大后减小，分别在墩梁连接方式等于1和3下达到最大值。7和8号桥墩墩底截面的面内弯矩随着墩梁约束方式的增加与加强而增大，其他桥墩墩底截面的面内弯矩随着墩梁约束方式的增加与加强的变化规律较复杂。

图13 纵桥向激励下的纵向位移Fig.13 The longitudinal displacement by the incentive along the bridge

图14 横桥向激励下的横向位移Fig.14 The transverse displacement by the incentive cross the bridge

图15 纵桥向激励下的桥墩墩底面内弯矩Fig.15 In－plane moment of the bottom of pier by the incentive along the bridge

图16 横桥向激励下的桥墩墩底面外弯矩Fig.16 Out－ plane moment of the bottom of pier by the incentive cross the bridge

横向反应谱作用下，中跨跨中截面的横向位移随着墩梁约束关系的增加与加强而减小。分别在墩梁连接方式等于4和7下，达到最大和最小值。7～9号桥墩墩顶横向位移随着墩梁约束关系的增加与加强先增大后减小。在墩梁连接方式等于6下达到最大值。7～9号和11～12号桥墩墩底截面的面外弯矩，随着墩梁约束方式的增加与加强先增大后减小。其他桥墩墩底截面的面外弯矩随着墩梁约束方式的增加与加强的变化规律较复杂。

4 结论

(1)在设计允许范围内改变曲线半径对桥梁的自振频率影响较小，桥梁墩高的改变以及墩梁约束方式的改变对桥梁的自振频率产生较大的影响。

(2)曲线半径在600～1200 m变化时，中跨跨中截面、桥梁墩顶截面的位移和墩底截面弯矩的地震响应变化非常小。

(3)在纵向反应谱作用下，桥墩墩高的改变对地震响应的变化规律比较复杂，在横向反应谱作用下，地震响应有一定的变化规律。

(4)总的来说，在纵、横向反应谱作用下，墩梁约束方式为约束7的地震响应最小，但综合考虑温度、制动力学因素，应该是原设计约束5最优。

［1］Tomohisa H，Taiji M，Hiaanori O.Analytical study on seismic performance of a continuous rigid frame bridge with unequal piers considering damage growth and energy absorption［C］//13th World Conference on Earthquake Engineering Conference Proceedings，2004.

［2］牛俊武，郭楠楠，马文涛.不同曲率半径对高墩大跨径连续刚构桥抗震性能影响分析［J］.公路，2011，(9):137－141.NIU JUNwu，GUO NANnan，MA WENtao.The seismic performance analysis of high piers and long span continuous rigid－frame bridge with different curvature radiuses［J］.Highway，2011，(9):137 －141.

［3］单德山，李乔.铁路曲线梁桥抗震设计分析［J］.重庆交通学院学报，2005，24(1):1－4.SHAN Desan，LI Qiao.Study of seismic design for railway curve－girder bridge［J］.Journal of Chong Qing Traffic Institute，2005，24(1):1 －4.

［4］彭凯，李建中，范立础.高墩梁桥考虑墩身高阶振动的水平向主导振型［J］.振动与冲击2008，27(7):37－67.PENG Kai，LI Jianzhong，FAN Li－ chu.The level dominant vibration modes of high piers bridge according to the high orders vibration of piers［J］.Vibration and Shock 2008，27(7):37－67.

［5］周勇军.高墩大跨曲线连续刚构桥梁地震响应的设计参数研究［D］.西安:长安大学，2006.ZHOU Yongjun.Study on design parameters affecting the seismic response of curved continuous rigid frame bridges with long－span and high－piers［D］.Xi＇an:Chang＇an University，2006.

［6］何钦象，田小红，宋丹.高墩大跨径连续刚构桥抗震性能评估［J］.振动与冲击2009，28(1):68－71.HE Qinxiang，TIAN Xiaohong，SONG Dan.Astigmatic performance evaluation of a long－span continuous rigid frame bridge with tall piers［J］.Journal of Vibration and-Shock，2009，28(1):68－ 71.

［7］王达，刘扬，陈敏海.超高墩大跨部分曲线连续刚构桥地震反应分析［J］.公路交通科技2011，28(1):74－79.WANG Da，LIU Yang，CHEN Min－hai.Seismic response analysis of partial curve long－span continuous rigid frame bridge with high piers［J］.Journal of Highway and Transportation Research and Development，2011，28(1):74－79.

［8］Wong P K C，Priestley M J N，Park R.Seismic resistance of frames with vertically distributed longitudinal reinforcement in beams［J］.ACI Structural Journal 1990，87(4):488－489.

［9］赵灿晖.大跨度桥梁地震响应分析中的非一致地震激励模型［J］.西南交通大学学报，2002，37(3):236－240.ZHAO Canhui.The Asynchronous excitation model for the seismic response analysis of Long－Span bridges［J］.Journal of Southwest Jiaotong University，2002，37(3):236－240.

［10］余玲玲，王解军.高墩大跨连续刚构桥的动力性能及地震反应分析［J］.公路工程，2008，33(1):36－38.YU Lingling，WANG Jiejun.Analysis of dynamic characteristics and seismic responses for high pier－long span continual rigid frame bridge［J］.Highway Engineering，2008，33(1):36－ 38.

［11］Dicleli M，Mansour M Y.Efficiency of seismic isolation for seismic retrofitting of heavy substructured bridges［J］.Journal of Bridge Engineering，2005(4).

［12］罗波夫.高速铁路桥梁弹塑性地震响应分析［D］.长沙:中南大学，2011.LUO Bofu.Elastic－plastic seismic response analysis of high－ speed railway bridge［D］.Changsha:Centeral South University，2011.

［13］GB 18306—2001，中国地震动区划图［S］.GB 18306—2001，China shock employed to map［S］.

［14］GB 50111—2006，铁路工程抗震设计规范［S］.GB 50111—2006，Code for seismic design of railway engineering［S］.